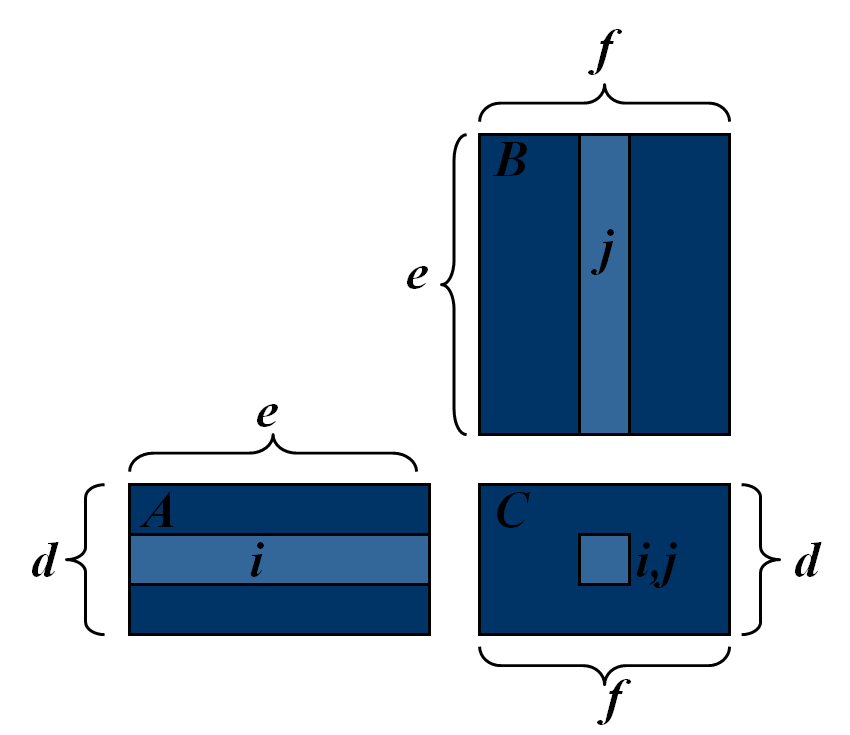
C = A * B
A : d e in B : e f
O(def)
Množenje zaporedja matrik
Množenje zaporedja matrik
Matija Lokar
Množenje matrik
Matrično množenje
Zaporedje množenj matrik:
- Izračunaj A=A*A*…*A
- A ima dimenzije d d
- Problem: Kako postaviti oklepaje?
Zanima nas NAČIN množenja in ne množenja sama!
Rezultat bo vedno enak
- Množenje matrik je asociativno!
- Problem je smiseln, če bomo večkrat množili matrike enakih dimenzij, a z različnimi vrednostmi!
- Vnaprej si pripravimo način množenja
Primer: B * C * D
- B :
- C :
- D :
Dve možnosti
- (B*C)*D : op + op = op
- B*(C*D) : op + op = op
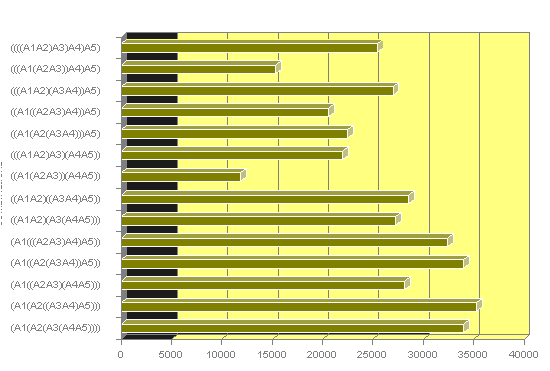
Množenje 5 matrik
| 
|
Preizkusimo vse
Algoritem:
- Na vse možne načine postavi oklepaje A=A*A*…*A
- Za vsak način izračunaj število operacij
- Izberi najboljšo
Čas:
- Možnih načinov postavljanja oklepajev je toliko, kot je dvojiških dreves z n listi, kjer ima vsako vozlišče (razen lista) dva sinova (Zakaj?)
- To je eksponentno!
- Dobimo t.i. Catalan-ovo število, ki je približno 4.
- Nemogoče slab algoritem!
Požrešni pristop
- Ideja: izberemo matriki z najmanj množenji.
Protiprimer:
- A :
- B :
- C :
- D :
Ideja
- AB: , BC: , CD:
- (B*C)
- A: , (BC): , D:
- A(BC): , (BC)D:
- ((B*C)*D) :
- (A*((B*C)*D))
- + + = op
- ((A*B)*(C*D))
- + + = op
Boljše!
- Je to najboljše možno?
Še en požrešni način
- Ideja: izberemo matriki, ki zahtevata največ operacij (da že na začetku "pokurimo požrešneže").
Protiprimer:
- A :
- B :
- C :
- D :
Naša ideja da: (A*B)*(C*D),
- + + = op
A*((B*C)*D)
- + + = op
Ideja – razmišljajmo rekurzivno
- Zadnja operacija bo zmnožila dve matriki
A = B * C
- B so “leve” matrike
- C so "desne" matrike
Če želimo, da je to optimalno, moramo tako do B, kot tudi do C, priti na optimalni način
- Pravilo optimalnosti
Vprašanje:
- Koliko matrik spada v B?
- Če znamo to vedno določiti – imamo rešitev
- Problem razpade na dva manjša problema ISTE vrste – rešimo enako
