V teh vajah si bomo ogledali nekaj primerov, ko naletimo na zelo velika števila. Videli bomo, kako hitra je eksponentna rast. Uporabili bomo zmožnost programa DERIVE, da zna računati s poljubno velikimi celimi števili. Še več. Če bomo hoteli, bomo videli prav vse števke teh velikih števil. Uporabili bomo podatke, ki ste jih pripravili. Najprej jih vpišite v tabelo.

Poglejmo, kako si bomo pomagali s programomDERIVE.

Vnos izraza:
Ko poženemo program ( DERIVE 6) zagledamo okno, kamor bomo vnesli izraz.

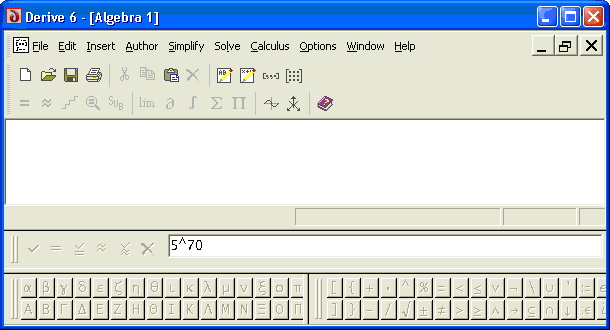
V različici 6 se postavimo v spodnjo vrsto, kjer vnašamo izraze. V programu DERIVE izraz 570 vnesemo kot 5^70. Do znaka ^ pridemo tako, da sočasno pritisnemo desni ALT (ALT Gr) in tipko 3. Znak se bo pojavil, če potem pritisnemo še preslednico. V različici DERIVE for Windows 6 ga lahko vnesete tudi tako, da kliknete na peti gumb v zgornji vrsti desne orodjarne, ki je na dnu zaslona.
Vnos izraza zaključimo s pritiskom na tipko Enter.

Točna vrednost izraza:

Če nas zanimajo vse števke številskega izraza, ta izraz najprej označimo tako, da nanj kliknemo z miško. Nato uporabimo ukaz Simplify/Basic (oziroma ikono ).

Približna vrednost izraza.

Če nas zanima le približna vrednost (zapisana v eksponentni obliki), izraz označimo in uporabimo Simplify/Approximate. V oknu

po potrebi spremenimo natančnost (Digits of precision) in kliknemo na gumb Approximate.

Vzemite list papirja formata A4. List prepognite na pol, še enkrat na pol, in še enkrat, itd. Kolikokrat lahko ponovimo prepogibanje? Iz tabele z začetka izračunajte debelino 1 lista. Po vsakem prepogibanju se debelina podvoji. Izpolnite tabelo, kako bi bil prepognjenec debel, če bi (teoretično) izvedli prepogibanj. Rezultate zaokroži na tri decimalna mesta natančno.

Preveri

Ugotovite (s poskušanjem), koliko prepogibanj bi potrebovali, da bi zložen list papirja segal približno

Preveri

Indijski vezir je bil tako navdušen nad igro šaha, da je izumitelju obljubil karkoli si le ta poželi. "Skromni" menih si je zaželel "le" toliko riža, kot ga je potrebno, če postavimo na prvo šahovsko polje eno zrno, na naslednje dve zrni, na tretje štiri, pa osem, itd. do zadnjega, 64. polja, na katerem bo zrn riža. Ugotovimo, koliko je to. Zaokroži na dve decimalni mesti natančno, kjer je potrebno.

Preveri

Znate ugotoviti, koliko tehta ves riž na šahovnici? Zaokroži na dve decimalni mesti natančno.

Ves riž na šahovnici tehta kg.

Preveri

Odgovorite še na ta vprašanja:

1. Denimo, da vsi prebivalci Slovenije začno jesti riž za zajtrk, kosilo in večerjo. Pri vsakem obroku vsak poje dag riža. Koliko dni bodo jedli riž, če jim je na voljo ves riž na polju

Koliko kg riža potrebujejo vsi Slovenci na dan?
Potrebujejo kg riža na dan.

Preveri

Preveri

2. Za koliko dni bi bili z rižem na zadnjih treh poljih preskrbljeni prebivalci Zemlje?

Prebivalci zemlje bi bili preskrbljeni za dni.

Preveri

Kolikšen kvader bi dobili, če bi zložili skupaj škatle z rižem, ki je na polju? Zaokroži na dve decimalni mesti natančno.

Volumen kvadra, ki ga dobimo, zajema prostornino .

Preveri

Kolikšno površino bi morali zasejati z rižem, da bi z eno žetvijo zadostili potrebam za polje? Zaokroži na dve decimalni mesti natančno.

Za riž na polju je potrebno zasejati milijonov ha.

Preveri

Vzemimo prvih pet naravnih števil in jih zmnožimo. Dobimo To število zapišemo kot in mu rečemo faktoriela števila ali fakulteta. Produktu prvih naravnih števil torej rečemo fakulteta in zapišemo kot

1!=!
(n+1)!=(n+1)* n!

Faktoriela zelo hitro raste. Izpolnite tabelo!

Preveri

Izpolnite tabelo, tako da bo veljalo

Preveri