Statistika - Relativna števila
Sistem za prikazovanje nujno potrebuje vključen Javascript.
Vaš brskalnik je zastarel
Gradiva nauk.si zahtevajo za pravilen prikaz sodoben brskalnik. Preverjeno delujejo
z brskalniki Mozilla Firefox 3.5+, Google Chrome 4.0+, Safari 4.0+, Internet Explorer 8.0+ ali Opera 10.50+.
V primeru, da uporabljate Internet Explorer 8, preverite, če imate vklopljen združljivostni način
(Compatibility view), ki ga lahko izklopite s klikom na ikono, ki jo vidite na spodnji sliki.
Povezave na najnovejše različice brskalnikov:
Prikaži vsebino
Statistika - Relativna števila
Avtor: inter-es (vsebinsko), Katja Markovič (tehnično)
Začni
Hvala za ogled gradiva!
Veseli bomo vaših komentarjev. Obiščite nas na www.nauk.si .
Začni znova
Uporabljeni viri
http://www.inter-es.si/met/
Pojem in vrste relativnih števil
Pri statističnih analizah se boste pogosto srečevali s primerjanjem podatkov:
uspeh študentov na izpitu lahko opišete tako, da poveste deleže po doseženih ocenah.
Zaposlene v podjetju opišete tako, da poveste deleže po strokotni izobrazbi, spolu, ...
Gospodarsko razvitost držav primerjate po brudo družbenem proizvodu na prebivalca.
Uspešnost trgovinske menjave opišete tako, da primerjate izvoz z uvozom.
Uspešnost komercialne službe opišete tako, da primerjate prodajo z zalogami.
Uspeh podjetja boste prokazali z ratjo prihodkov.
Naprej
Pri primerjavi podatkov delimo dva istovrsta ali raznovrsta podatka. Količnik je relativno število.
Od tu tudi ime za izračunane parametre: relativna števila .
Naprej
Pojem in vrste relativnih števil
V nadaljevanju boste spoznali relativna števila, ki jih boste najpogosteje uporabljali v statističnem proučevanju ali na nje naleteli pri poslušanju in branju dnevnih informacij.
Najpogostejša relativna števila so:
Naprej
Strukture
Naprej
So relativna števila, ki jih dobite, ko delite del s celoto in so običajno izražene v odstotkih.
Primer
V Sloveniji uporablja internet 33 % prebivalcev.
Statistični koeficienti
Naprej
So relativna števila, ki jih dobite, ko delite dva raznovrstna podatka .
Primer
V Sloveniji je bil v letu 2004 bruto družbeni proizvod 13000 EUR/prebivalca.
Indeksi
Naprej
So relativna števila, ki jih dobite, ko delite dva istovrstna podatka in so običajno izražena s procenti.
Primer
Indeks rasti plač v januarju glede na januar prejšnjega leta je 105 %.
Naprej
Strukture
Če zberete podatke le o eni lastnosti enot populacije, se taka struktura imenuje enorazsežna struktura .
Naprej
Strukture
V excelovi datoteki enorazseznastruktura.xlsx so zbrani podatki o strokovni izobrazbi zaposlenih.
Izračunajte strukturo zaposlenih tako, da v celice tretjega stolpca vpišete obrazec za izračun strukture ( = število po stopnjah / število vseh zaposlenih).
Naprej
Strukture
Stukturo prikažite z odstotki!
Naprej
Dvorazsežna struktura
Če zberete podatke o dveh lastnostih enot populacije, se taka struktura imenuje dvorazsežna struktura .
Primer
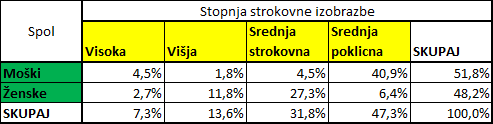
V tabeli so zbrani podatki o zaposlenih v podjetju A po strokovni izobrazbi in spolu. Lahko si prenesete tudi excelovo datoteko dvorazseznastruktura.xlsx , ki vsebuje te podatke.
Naprej
Izračunajte strukturo zaposlenih po stopnji izobrazbe in spolu ter podatke v odstotkih vpišite v ustrezne celice tabele.
Preglej
Dvorazsežna struktura
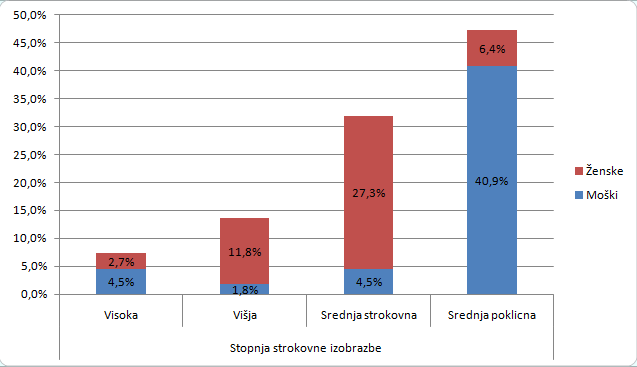
Za grafično prikazovanje dvorazsežnih struktur je primeren stolpični grafikon.
Interpretirajte strukturo zaposlenih, ki jo prikazuje grafikon, narisan na podlagi prejšnjega primera.
Naprej
Statistični koeficienti
Statistične koeficiente boste uporabljali za primerjavo dveh raznovrstnih podatkov, katerih primerjava je vsebinsko smiselna in ima neko analitično vrednost za proučevano populacijo.
Naprej
Po družbenem produktu na prebivalca lahko presojate gospodarsko razvitost države, regije. Po številu avtomobilov na tisoč prebivalcev presojate življenjsko raven prebivalstva.
Naprej
Statistični koeficienti so lahko kazalniki usprešnosti poslovanja.
Uspešnost poslovanja podjetij ocenjujemo po kazalnikih , ki jih predpisujejo računovodski standardi, npr.:
Naprej
delež dolgov v financiranju (dolgovi: obveznosti do virov sredstev),
Naprej
delež osnovnih sredstev (osnovna sredstva / sredstva),
Naprej
kapitalska pokritost dolgoročnih sredstev (capital / dolgoročna sredstva),
Naprej
razmerje med komercialnimi terjatvami in obveznostmi (terjatve do kupcev / obveznosti do dobaviteljev),
Naprej
gospodarnost poslovanja (prihodki od poslovanja / odhodki od poslovanja)
Naprej
Statistični koeficienti
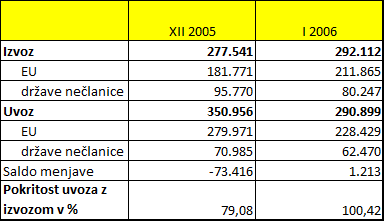
Tabela prikazuje podatke o izvozu in uvozu Slovenije, ki jih mesečno objavlja Statistični urad RS na sletnih straneh.
Izvoz in uvoz Slovenije v mio. SIT
Naprej
Kazalnik pokritosti uvoza z izvozom se izračuna:
Pokritje uvoza z izvozom =
Naprej
Koeficient obračanja zalog
V trgovskih in proizvodnih podjetjih je uspešnost poslovanja odvisna od zalog. Podjetja si prizadevajo, da so zaloge optimalne. Gibanje zalog izražajo s koeficientom obračanja zalog , ki predstavlja:
količnik med vrednostjo prodaje in vrednostjo povprečne zaloge trgovskega plaga;
Naprej
v proizvodnji pa lahko količnik med vrednostjo porabljenih surovin in vrednostjo povprečne zaloge.
Naprej
Pri izračunu koeficienta obračanja zalog morate biti pozorni na časovno opredelitev podatkov. Slednji so lahko trenutni ali intervalni .
trenutni podatek spremenite v intervalnega z računanjem povprečja .
Naprej
Koeficient obračanja zalog - Primer
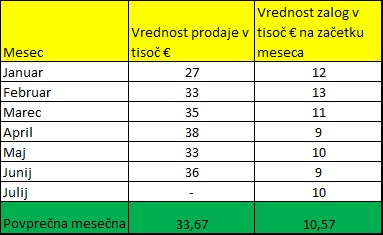
V tabeli so zbrani podatki o prodaji za prvo polletje po mesevih in o zaloga na začetku meseca.
Prodaja in zaloge v prvem polletju
Naprej
Na naslednjih straneh bomo skupaj izračunali:
mesečni koeficient obračanja zalog v prvem polletju in
povprečno število dni skladiščenja blaga, če je v mesecu 25 delovnih dni.
Naprej
Koeficient obračanja zalog - Izračun mesečnega koeficienta zalog K
Izračunajmo mesečni koeficient obračanja zalog v prvem polletju.
Prikaži tabelo
Izračunajte povprečno mesečno prodajo za prodajo za prvo polletje tako, da vsoto prodaj po mesecih delite s številom mesecev.
Naprej
Izračunajte povprečno mesečno zalogo za prvo polletje. Tu morate trenutnw podatke (zaloge ob začetku meseca) spremeniti v intervalne (povprečje za posamezni mesec). To naredite tako, da za vsak mesec izračunate vsoto začetnih in končnih zalog (začetek naslednjega meseca) in delite z 2.
Naprej
Izračunate povprečne mesečne zaloge za prvo polletje tako, da vsoto povprečnih mesečnih zalog delite s številom mesecev.
Naprej
Izračunajte mesečni koeficient zalog K!
V enem mesecu se zaloge 3,2-krat obrnejo.
Naprej
Koeficient obračanja zalog - Izračun povprečnega števila dni skladiščenja blaga
Drugi del naloge od vas zahteva, da izračunate povprečno število dni skladiščenja blaga .
Naprej
Na hitro lahko ocenite, da je to 8 dni. Izračunate pa tako, da izračunate recipročni (obratni) koeficient obračanja zalog , ki vam pove čas enega obrata oziroma čas skladiščenja blaga.
Naprej
Zaloge so se obrnile v 0,3125 meseca, oziroma pri 25 delovnih dnevih v:
Naprej
Indeks
Indeks je relativno število, ki ga dobite tako, da delite dva istovrstna podatka statistične vrste. Količnik običajno izrazimo v %.
Naprej
Krajevni indeks
Če se indeksi nanašajo na geografska področja, so to krajevni indeksi .
Naprej
Časovni indeks
Če se podatki nanašajo na spreminjanje pojava v času, imenujemo te indekse časovne indekse .
Naprej
Najprej delimo časovne indekse na:
Časovni indeks - indeks s stalno osnovo
Statistični urad RS na spletnih straneh objavlja podatke o gibanju plač, cen, izvozu, ...
Na podlagi podatkov so običajno izračunani indeksi, ki jih dobite, če istovrstne podatke primerjate za različna obdobja.
Naprej
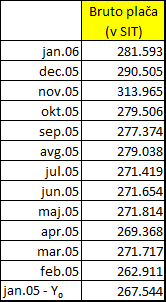
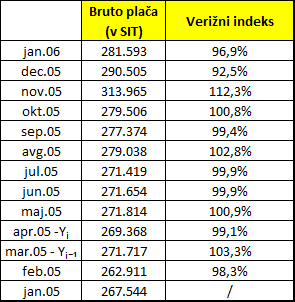
V tabeli so podatki o povprečnih bruto plačah v Sloveniji od januarja 2005 do januarja 2006.
Naprej
Časovni indeks - indeks s stalno osnovo
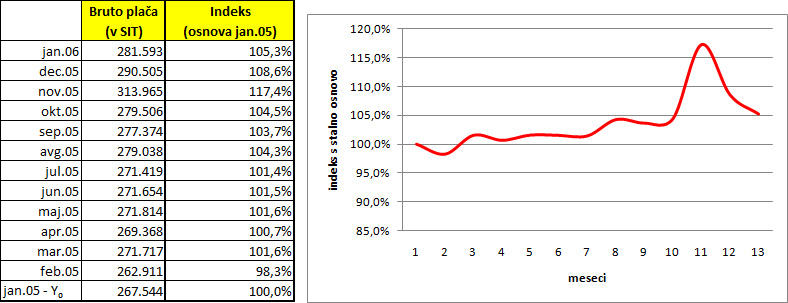
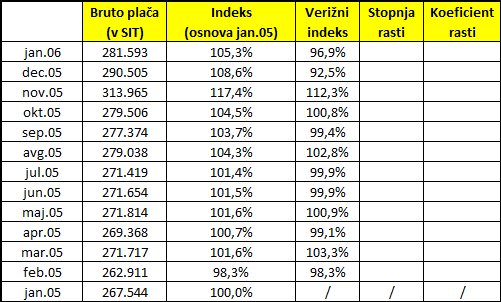
Indeksi prikazujejo rast plač po mesecih glede na januar 2005. Izraženi so v odstotkih.
Naprej
Če ste primerjali bruto plačo v januarju 2005 z bruto plačami v naslednjim mesecih, ste plače v posameznih mesecih delili s plačo v januarju 2005 .
Indeksi večji od 100 povedo, da so bile plače višje od januarske, manjši od 100, pa da so bile nižje od januarske.
Takšne indekse imenujemo indeksi s stalno osnovo in jih najboljše prikazujemo z linijskim grafikonom .
Izračunamo jih po naslednjem obrazcu:
Naprej
Časovni indeks - verižni indeks
Če podatek (npr. plača) v tekočem časovnem obdobju (npr. mesec) delite s podatkom v predhodnem časovnem obdobju, dobite verižni indeks.
Naprej
Časovni indeks - verižni indeks
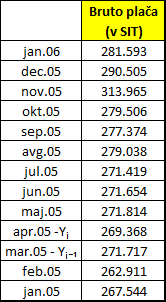
Verižni indeksi prikazujejo spremembo plač glede na prejšnji mesec. Izraženi so v odstotkih.
Naprej
Če primerjate plači med dvema zaporednima mesecema, računate verižni indeks. Plačo v tekočem mesecu delite s plačo v predhodnem mesecu. Če je vrednost indeksa večja od 100, pomeni, da se je plača povečala. Če pa je vrednost indeksa manjša od 100, pomeni, da se je plača zmanjšala, seveda vedno v primerjavi s prejšnjim mesecem.
Naprej
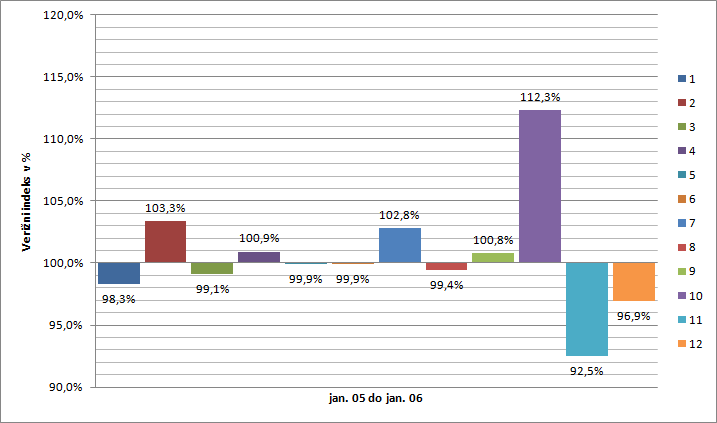
Časovni indeks - verižni indeks
Verižne indekse običajno grafično prikažemo s stolpičnim grafikonom.
Naprej
Verižni indeks izračunate po naslednjem obrazcu:
Naprej
Koeficient rasti in stopnja rasti
Poleg indeksov uporabljamo pri proučevanju rasti pojavov še nekatere druge kazalnike, ki pa so na en ali drug način povezani z indeksi. Pomembni so predvsem pri proučevanju sprememb med dvema zaporednima časovnima obdobjema.
Naprej
Koeficient rasti dobimo, če primerjamo dva zaporedna podatka časovne vrste.
Naprej
Za izražanje spremembe med dvema zaporednima podatkoma časovne vrste uporabljamo stopnjo rasti .
Izračunate jo tako, da razliko med dvema zaporednima podatkoma časovne vrste delite s predhodnim podatkom ter množite s 100, da dobite izraženo v %:
Naprej
Koeficient rasti in stopnja rasti
Najbrž ste že opazili, da sta koeficient in stopnja rasti povezana s verižnim koeficientom:
verižni indeks - 100 = stopnja rasti
verižni indeks : 100 = koeficient rasti
Naprej
Prav tako sta med seboj povezana tudi koeficient in stopnja rasti:
(koeficient rasti - 1) stopnja rasti
Primer
Koeficient rasti in stopnja rasti
Primer
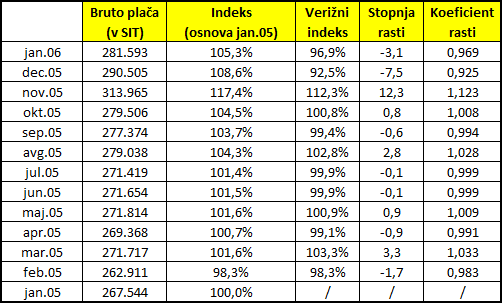
Izračunajte stopnje in koeficiente rasti! Za lažje reševanje si naložite datoteko place.xslx .
Rešitev
Rešitev