Graf funkcije
Oglejmo si funkcijo Definirana je za vsa realna števila razen za . Poskusimo jo narisati. Pri risanju bomo upoštevali, da je funkcija soda.
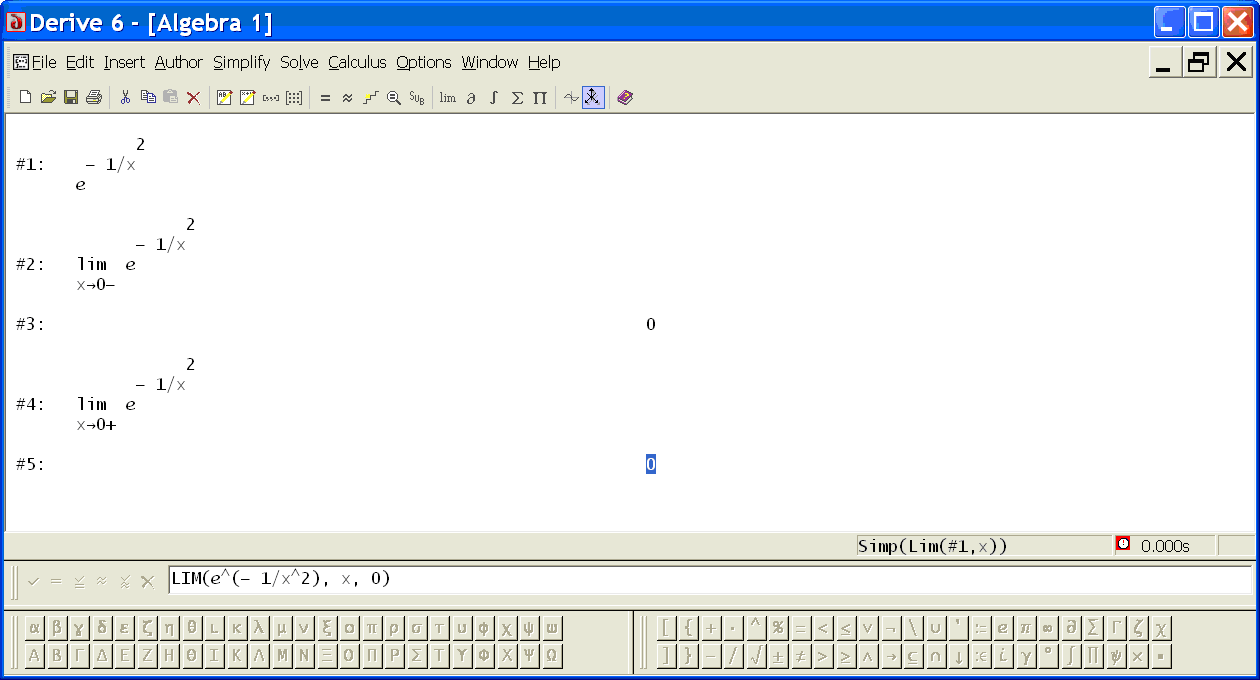
Najprej zapišimo našo funkcijo:
| e^(-1/x^2) |
Tabelirajmo funkcijo na intervalu .
| Simplify/Variable Substitution x=1 |
| Simplify |
Zamenjajmo še z , , , , ter izračunajmo numerično vrednost funkcije pri takih -ih.
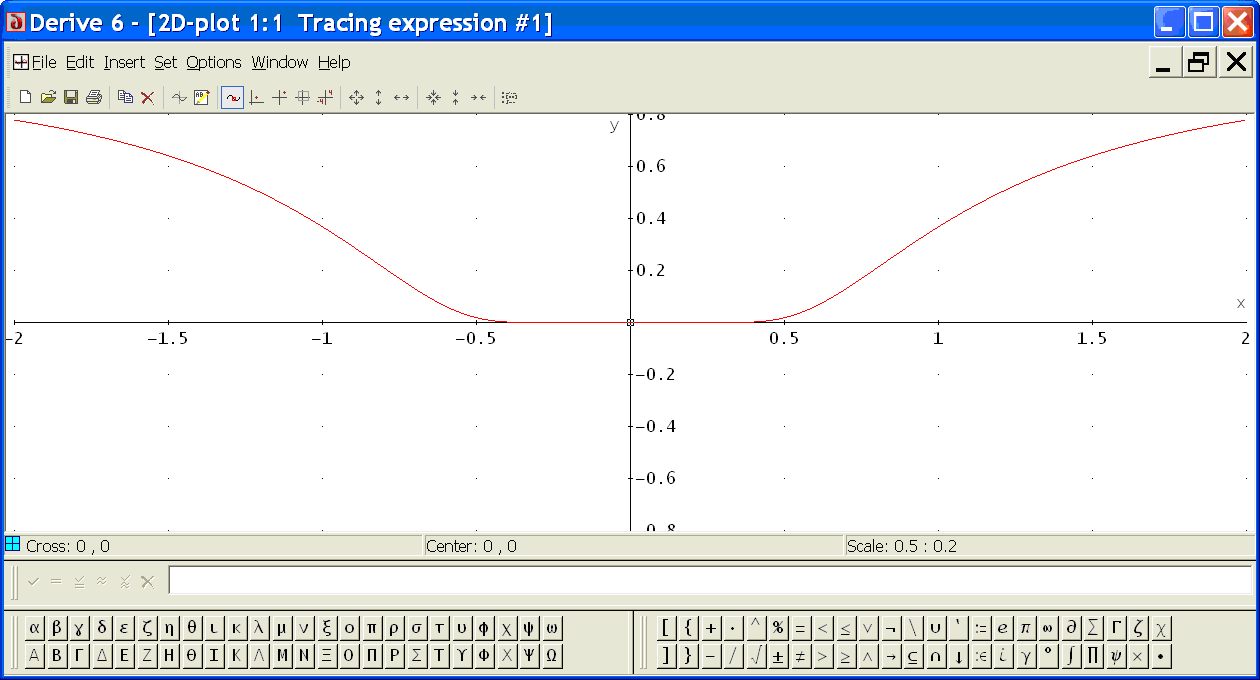
S pomočjo tabele skicirajmo graf funkcije na tablo. Za sliko "pravega" grafa si spet lahko pomagamo s programom Derive.
| Plot |
Izračun limite
Ko končamo z risanjem funkcije, se vrnemo v algebrajsko okno
| Algebra |
Lepo vidimo (računsko in s pomočjo grafa), da se vrednost funkcije približuje (teži) k , ko se k približuje (ni važno s katere strani: pozitivne ali negativne).
Limito funkcije lahko tudi izračunamo.
| Calculus/Limit |
| Simplify (dobimo točen rezultat) ali |
| Approximate (rezultat je decimalno število) |
Limite danih funkcij
Kaj je torej limita funkcije? Poskusimo z laično definicijo.
Nato si poglejmo, kako je z limitami danih funkcij.
| FUNKCIJA | VNOS ZA DERIVE | V TOČKI |
| x^3-3x^2+4 | ||
| (x^2+x-6)/(x+3) | ||
| 1/(x-1)^2 | ||
| 1/(x-1) | ||
| IF(x>1,x+2,1-x) | ||
| IF(x=5,3,10) |
Še predno "resno" začnemo z delom, si oglejmo, kako je s funkcijo v tisti točki, kjer želimo izračunati limito (je ali ni definirana), kako se spreminja vrednost funkcije okoli limitne točke.
Pomagajmo si s programom Derive.
Postopek
| 1) | Vnesimo funkcijo. | ||
| |||
| 2) | Funkcijo tabeliramo v okolici točke, kjer limito iščemo. | ||
| (Opazovani povečujmo in zmanjšujmo za , , , , , …) | |||
| |||
| |||
| Kaj lahko pričakujemo za limito? | |||
| 3) | Narišimo graf funkcije. | ||
| a) | "Premaknimo" se v okno za risanje grafov. | ||
| |||
| b) | Zbrišimo narisane grafe (če jih ni, ta korak spustimo). | ||
| |||
| c) | Narišimo graf naše funkcije. | ||
| |||
| d) | Končajmo z risanjem funkcije. | ||
|
Ali smo spremenili naša pričakovanja o limiti funkcije v izbrani točki?
Postopek
| 4) | Poglejmo, kam se približuje vrednost funkcije, če se limitni točki približujemo z leve strani. | ||
| |||
| |||
| 5) | Poglejmo, kam se približuje vrednost funkcije, če se limitni točki približujemo z desne strani. | ||
| |||
| |||
| 6) | Izračunajmo še limito funkcije. | ||
| |||
|
