Pritisnite F11

Iz varnostnih razlogov je mogoče celozaslonski način vključiti samo s pritiskom na gumb F11 na tipkovnici.

Ko ste enkrat v celozaslonskem načinu, ga izključite spet s pritiskom na F11.

Trikotnik

Avtor: E-um (vsebinsko), Skupina NAUK (tehnično)

Sodelujoče organizacije

Izvedbo projekta je omogočilo sofinanciranje Evropskega socialnega sklada Evropske unije in Ministrstva za šolstvo in šport. Pri tehnični izvedbi projekta so sodelovali: Fakulteta za matematiko in fiziko Univerze v Ljubljani, Inštitut za matematiko, fiziko in mehaniko in podjetje Hruška d.o.o.

Hvala za ogled gradiva!

Veseli bomo vaših komentarjev. Obiščite nas na www.nauk.si.

Uporabljeni viri

E-um

www.e-um.si

Sodelujoče organizacije

Izvedbo projekta je omogočilo sofinanciranje Evropskega socialnega sklada Evropske unije in Ministrstva za šolstvo in šport. Pri tehnični izvedbi projekta so sodelovali: Fakulteta za matematiko in fiziko Univerze v Ljubljani, Inštitut za matematiko, fiziko in mehaniko in podjetje Hruška d.o.o.

Uvod

Trikotna oblika daje občutek trdnosti in varnosti. Srečamo jo v arhitekturi in umetnosti, glasbi in tehniki.

Opis slik

Vidimo jih na oddihu in potovanju, pri rekreaciji in zabavi

Opis slik

Ti je beseda triangulacija znana?

Opazovalec na obali lahko izračuna, koliko je jadrnica oddaljena od obale.

Triangulacija je postopek, s katerim lahko rešimo mnoge zagate.

Kako bi lahko izračunali oddaljenost $d$ ladje od obale? Opazovalec v oglišču $A$ izmeri kot $\alfha$ med obalo in ladjo, opazovalec v oglišču $B$ naredi podobno. Razdaljo $d$ lahko iz obeh izmerjenih kotov in znane razdalje $l$ med obema opazovalcema izračunamo z uporabo kotnih funkcij.

Triangulacijo uporabljajo tudi geodeti pri meritvah.

Nekatere fotografije so nastale na potovanjih, druge pa so v javni lasti na spodaj navedenih spletnih straneh.

Slika 1: Grški timpanon (zgornji del templja) ima značilno trikotno obliko.

Slika 2: V renesansi so umetniki pogosto uporabljali trikotno kompozicijo. Trikotna kompozicija na zgornji sliki je dvojna (glej modre in rdeče črte na sliki). Med vrhovoma obeh trikotnikov je božja podoba, pod njo pa Jezus. (http://www.wga.hu/index1.html)

Slika 3: Triangel je glasbeni instrument, s katerim se večina otrok sreča že v vrtcu. (http://store.drumbum.com/media/triangle-6-inch-quality.jpg)

Slika 4: Leonardo Da Vinchi si je zamislil padalo, sešito iz trikotnih delov. (http://www.museoscienza.org/leonardo/invenzioni/paracadute.asp)

Slika 5: Pri glasbenih stolpih je stabilnost zelo pomembna, saj se tako zmanjšajo vibracije in je zvok čistejši. Kot že vemo, so za natančno določitev ravnine potrebne tri točke. Zato pri mizah s tremi nogami nimamo težav s tem, da bi se majale. Če pa ima miza štiri noge, se kaj rado zgodi, da moramo eno nogo podložiti. (http://www.shopolina.com/-/Y=MALBORET-MIZA-HIFI-MDF-4P-CRNA--i-3-IPPOWEYP/)

Slika 1: Lesene hišice, ki imajo sprednjo stran v obliki trikotnika, ponujajo za prenočevanje na estonskem otoku Kuresare.

Slika 2: Rdeče obrobljena trikotna oblika prometnega znaka naznanja nevarnost. Na Baltiku lahko na cesto pritečejo tudi losi.

Slika 3: Jadrnica, s katero so jadrali dijaki na šolskem taboru v Piranu, je imela dve trikotni jadri.

Slika 4: Veliko lesenih nosilnih konstrukcij je trikotnih. Takšna je tudi nosilna konstrukcija gugalnice na sliki.

Kaj že vem?

Dovolj klepetanja. Mislim, da je skrajni čas, da začnemo z resnejšim delom. Za začetek ponovimo, kar smo se o trikotniku naučili v osnovni šoli. Na spodnji sliki poveži zelene točke ob premicah, daljicah, točkah in kotih z ustreznimi opisi na desni strani. Kako? Točko primi in potegni z miško.


Aplikacija RiŠ se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)
Riš datoteka

Trikotnik je geometrijski lik, ki ga določajo tri nekolinearne točke, ki so med seboj povezane z daljicami.

Kaj že vem?

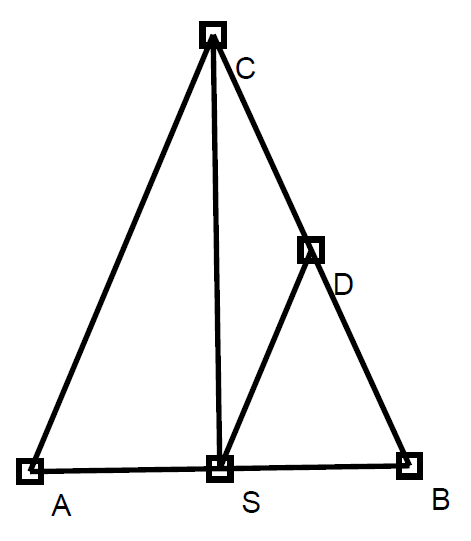
Tri točke, ki določajo trikotnik, imenujemo oglišča, daljice, ki jih povezujejo, pa so stranice.

Oglišča označujemo z velikimi tiskanimi črkami. Če si oglišča sledijo v smeri, ki je nasprotna vrtenju kazalcev na uri, pravimo, da je trikotnik pozitivno orientiran, če pa si oglišča sledijo v isti smeri, kot tečejo kazalci na uri, pa govorimo o negativni orientaciji.

Stranice označujemo z malimi tiskanimi črkami in po dogovoru se stranica imenuje enako kot oglišče, ki ji leži nasproti.

Kote pri ogliščih trikotnika imenujemo notranji koti, njihove sokote pa zunanji koti. Ko rišemo zunanje kote, si pomagamo z nosilkami stranic. To so premice, na katerih ležijo stranice trikotnika.

Notranje kote označujemo s pisanimi črkami GRŠKE abecede. Oznaka kota se ujema z oznako oglišča, ki je vrh kota.

Zunanje kote označujemo enako kot notranje, le da jim dodamo desno zgoraj majhno vejico.

Premice, na katerih ležijo dane stranice, imenujemo nosilke stranic.

Kote v trikotniku označujemo s pisanimi črkami Grške abecede

Med trikotniki posebej poimenujemo tiste, ki so glede na podatke nekaj posebnega.

Enakokraki trikotnik ima dve enako dolgi stranici—kraka. Tretjo stranico imenujemo osnovnica. V enakokrakem trikotniku sta kota ob osnovnici skladna.

Enakostranični trikotnik ima enako dolge vse tri stranice in enako velike vse notranje kote.

Pravokotni trikotnik ima en pravi kot.

Grška abeceda, njeni ekvivalenti in izgovorjava:

Grška črka	Ekvivalent v latinici	Izgovorjava
$\alpha$	$a$	[alfa]
$β$	$b$	[beta]
$γ$	$g$	[gama]
$δ$	$d$	[delta]
$ε$	$e$	[epsilon]
$ζ$	$z$	[zeta]
$η$	$e$	[eta]
$θ$	$th$	[theta]
$ι$	$i$	[iota]
$κ$	$k$	[kapa]
$λ$	$l$	[lambda]
$μ$	$m$	[mi]
$ν$	$n$	[ni]
$ξ$	$x$	[ksi]
$ο$	$o$	[omikron]
$π$	$p$	[pi]
$ρ$	$r$	[ro]
$ς$	$s$	[sigma]
$τ$	$t$	[tau]
$υ$	$u$	[ipsilon]
$φ$	$ph$	[fi]
$χ$	$ch$	[hi]
$ψ$	$ps$	[psi]

Stranice in koti v trikotniku

V nadaljevanju se bomo spomnili nekaterih pomembnih rezultatov v zvezi s stranicami in koti v trikotniku Na spodnjem apletu premikaj oglišče $C$ , tako da boš dobil enakokrak trikotnik, s krakom $a = b$ dolžine $5$ cm. (Pomagaj si z meritvami ob strani.)

S premikanjem točk poišči pravokotni trikotnik s pravim kotom v oglišču $C$ in hipotenuzo dolžine $5$ cm.

Postavi točke tako, da bo nastal enakostranični trikotnik s stranico $5$ cm.

Se spomniš katerega od njih?


Aplikacija RiŠ se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)
Riš datoteka

Stranice in koti v trikotniku

Dopolni trditve.

Vsota dolžin dveh stranic je vedno enaka manjša večja od dolžine tretje stranice.

Vsota velikosti notranjih kotov v trikotniku je $º$ .

Vsota velikosti zunanjih kotov v trikotniku je $º$ .

Velikost zunanjega kota v trikotniku je enaka produktu razliki vsoti notranjih dveh nepriležnih kotov.

V trikotniku leži nasproti največjega kota enaka najkrajša najdaljša stranica.

Trditev, ki govori o povezavi med dolžinami stranic trikotnika, se glasi: vsota dolžin dveh stranic je vedno večja od tretje stranice. Temu pravilu pravimo trikotniška neenakost.

Zapomni si, da je velikost zunanjega kota v trikotniku enaka vsoti velikosti notranjih dveh nepriležnih kotov.

Obe pravili bomo kasneje preverili.

Preveri

Pravilno

Bravo. Na vsa vprašanja si odgovoril pravilno.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Preberi si rešitev.

Vsota dolžin dveh stranic je vedno večja od dolžine tretje stranice.

Vsota velikosti notranjih kotov v trikotniku je $180º$ .

Vsota velikosti zunanjih kotov v trikotniku je $360º$ .

Velikost zunanjega kota v trikotniku je enaka vsoti notranjih dveh nepriležnih kotov.

V trikotniku leži nasproti največjega kota najdaljša stranica.

O notranjih kotih? Zunanjih kotih? Stranicah? Če ne, nič hudega.

S premikanjem oglišč razišči, katere povezave obstajajo. Opazuj, kako je velikost poljubnega zunanjega kota povezana z vsoto velikosti notranjih dveh nepriležnih kotov in kakšna je zveza med največjim kotom in najdaljšo stranico ter najmanjšim kotom in najkrajšo daljico. Kaj pa če sta dva kota enako velika?

Ponovimo najpomembnejša dejstva

V vsakem trikotniku je vsota dolžin dveh stranic večja od dolžine tretje stranice.
Najdaljši stranici nasproti leži največji kot, najkrajši stranici nasproti pa leži najmanjši kot. Skladnima stranicama nasproti ležita skladna kota.
Vsota notranjih kotov v trikotniku je enaka $180º$ .
Vsota zunanjih kotov trikotnika je $360º$ .
Velikost zunanjega kota v trikotniku je enaka vsoti velikosti notranjih dveh nepriležnih kotov.

Vsota notranjih kotov v trikotniku

To, da je vsota notranjih kotov v trikotniku enaka $180º$ , lahko hitro pokažemo.

Spomnimo se izmeničnih kotov. Dobimo jih, če dve vzporedni premici presekamo s tretjo premico. Izmenična kota sta v pasu med vzporednicama na različnih straneh sekajoče premice in sta skladna.

Na spodnji sliki narišimo skozi oglišče $C$ vzporednico stranici $a$ in označimo (z isto barvo in črko) kotoma $\alpha$ in $\beta$ skladna izmenična kota. Vidimo, da je vsota kotov ob narisani premici enaka $180º$ , in ker sta kota $\alpha *$ in $\beta *$ skladna s kotoma $\alpha$ in $\beta$ , sklepamo, da je vsota notranjih kotov v trikotniku $\alpha+\beta + \gamma = 180º$ .


Aplikacija RiŠ se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)
Riš datoteka

Posebni primeri trikotnikov

Preveri svoje znanje

1. Če za notranje kote trikotnika velja $\alpha : \beta : \gamma = 1 : 2 : 3$ , potem koti merijo $20º$ , $40º$ in $60º$ .

Napačno. Pravilno.

2. Dan je pravokotni trikotnik. Če s S označena točka na hipotenuzi predstavlja vrh enakokrakega trikotnika ASC, tedaj je $\alpha = \beta$ . (Točka $S$ na apletu je premična. Tako lahko vidiš, da pravilo velja za poljuben pravokotni trikotnik, če le točka $S$ ustreza zapisanemu pogoju.)


Aplikacija RiŠ se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)
Riš datoteka

Napačno. Pravilno.

3. Koliko meri kot ob osnovnici enakokrakega trikotnika, če veš, da meri kot ob vrhu $70º$ ?

Namig

$110º$

$55º$

$70º$

4. Koliko merijo notranji koti enakokrakega pravokotnega trikotnika?

Namig

$90º,\ 90º ,\ 1º$

$45º,\ 90º,\ 45º$

Ker ni podan noben kot, ni mogoče rešiti naloge.

$60º,\ 60º,\ 60º$

5. Na spodnji sliki je nad kvadratno hišo postavljena streha v obliki enakostraničnega trikotnika. Koliko meri narisani kot $\alpha$ ?


Aplikacija RiŠ se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)
Riš datoteka

Namig

$60º$

$75º$

$80º$

Preveri

Pravilno

Bravo. Na vsa vprašanja si odgovoril pravilno.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Preberi si rešitev.
1. Če za notranje kote trikotnika velja $\alpha : \beta : \gamma = 1 : 2 : 3$ , potem koti merijo $20º$ , $40º$ in $60º$ .

Pravilno. Vsota notranjih kotov mora biti 180º.

2. Dan je pravokotni trikotnik. Če s S označena točka na hipotenuzi predstavlja vrh enakokrakega trikotnika ASC, tedaj je $\alpha = \beta$ . (Točka $S$ na apletu je premična. Tako lahko vidiš, da pravilo velja za poljuben pravokotni trikotnik, če le točka $S$ ustreza zapisanemu pogoju.)

Pravilno. Kota sta enako velika, saj je točka $S$ , ki je enako oddaljena od oglišč $A$ in $C$ , obenem tudi središče pravokotnemu trikotniku očrtane krožnice (ker leži na presečišču simetrale stranice $CA$ in hipotenuze) in je torej $d(A,S) = d(B,S) = d(C,S) = a$ . Od tod vidimo, da je trikotnik $BCS$ enakokrak. Njegova osnovnica je stranica $BC$ , kota ob njej $\alpha$ in $\beta$ pa sta skladna.

3. Koliko meri kot ob osnovnici enakokrakega trikotnika, če veš, da meri kot ob vrhu $70º$ ?

Kot meri $55º$ .

Preizkus: $55º+55º+70º=180º$ .

4. Koliko merijo notranji koti enakokrakega pravokotnega trikotnika? Koti merijo: $45º, 90º, 45º$ .

5. Na spodnji sliki je nad kvadratno hišo postavljena streha v obliki enakostraničnega trikotnika. Koliko meri narisani kot $\alpha$ ?

Narisani kot meri $75º$ .

Ker je trikotnik $ACV$ enakokrak in meri kot v oglišču $C$ $150º$ , sta kota ob osnovnici velika vsak po $15º$ . Ker je $\alpha$ zunanji kot trikotnika $CPV$ , je njegova velikost enaka vsoti notranjih dveh nepriležnih kotov: $60º + 15º = 75º$

Kota ob osnovnici sta skladna, vsota notranjih kotov v trikotniku pa je $180º$ .

En kot je gotovo $90º$ . To ne more bit kot ob osnovnici (razmisli zakaj).

Torej nam za kota ob osnovnici, ki sta skladna ostane še $90º$ .

Pozoren bodi na enakokrak trikotnik $ACV$ , kateraga kot ob vrhu $C$ meri $90º+60º=150º$ .

Naloga 1

Katere trojice spodaj zapisanih števil lahko predstavljajo dolžine stranic trikotnika? Katere od zapisanh trojic predstavljajo dolžine stranic enakokrakega trikotnika?

$3,\ 5,\ 7$

$5,\ 5,\ 20$

$13,\ 7,\ 3$

$10,\ 7,\ 3$

$5,\ 7,\ 5$

Počisti

Dolžine stranic trikotnika.

Ne morejo predstavljati ničesar od naštetega.

Dolžine stranic enakokrakega trikotnika.

Preveri

Pravilno

Pravilno si povezal.

Napačno

Mogoče je, da so nekateri izmed tvojih ujemanj pravilni, vendar ne vsi. Poskusi še enkrat.

Napačno

Mogoče je, da so nekateri izmed tvojih ujemanj pravilni, vendar ne vsi. Preberi si rešitev.

Rešitev: Dolžine stranic trikotnika so lahko števila $3,\ 5,\ 7$ in $5,\ 7,\ 5$ . Dolžine stranic enakokrakega trikotnika so lahko le števila pod točko $5,\ 7,\ 5$ .

Naloga 2

Izračunaj neznane notranje in zunanje kote trikotnika $ABC$ , če veš, da je $\alpha = 25°13´$ in $\beta ′ = 94°50´$ . Katera stranica v tem trikotniku je najdaljša in katera najkrajša?

Rešitev:

$\beta =$ $°$ $´$

$\gamma =$ $°$ $´$

$\alpha ´ =$ $°$ $´$

$\gamma ´=$ $°$ $´$

Najdaljša je stranica $a$ $b$ $c$ , najkrajša pa stranica $a$ $b$ $c$ .

Preveri

Pravilno

Bravo. Na vsa vprašanja si odgovoril pravilno.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Preberi si rešitev.
Rešitev:
$\beta = 85°10´$

$\gamma = 69°37´$

$\alpha ´ = 154°47´$

$\gamma ´= 110°23´$

Najdaljša je stranica b (nasproti največjega kota), najkrajša pa stranica a (nasproti najmanjšega kota).

Naloga 3

V trikotniku meri zunanji kot $\beta ′ = 120°$ , kota $\alpha$ in $\gamma$ pa sta v razmerju $5 : 7$ .

Izračunaj velikosti vseh notranjih in zunanjih kotov tega trikotnika.

$\alpha =$ $°$

$\beta =$ $°$

$\gamma =$ $°$

$\alpha ´ =$ $°$

$\gamma ´=$ $°$

Preveri

Pravilno

Bravo. Na vsa vprašanja si odgovoril pravilno.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Preberi si rešitev.

Rešitev:

$\alpha = 50°$

$\beta = 60°$

$\gamma = 70°´$

$\alpha ´ = 130°$

$\gamma ´= 110°$

Naloga 4

Dan je enakokraki trikotnik $ABC$ . (Glej sliko.) Točka $S$ je razpolovišče osnovnice $AB$ , točka $D$ pa je razpoloviščce kraka $BC$ . Kot $\angle SDC$ meri $130°$ .

a) Zapiši velikosti notranjih kotov trikotnika.
- $\alpha =$ $°$ , $\beta =$ $°$ , $\gamma =$ $°$
b) Zapiši vse enakokrake trikotnike, ki jih vidiš na sliki.
- Enakokraki trikotniki so:
  
  $ABC$
  
  $SBD$
  
  $CSD$
  
  $SBC$
  
  $ASC$
c) Kako velik bi moral biti kot $\angle SDC$ , da bi bil trikotnik $ABC$ enakostraničen?
- Da bi bil trikotnik $ABC$ enakostraničen, bi moral kot $\angle SDC$ meriti $°$ .

Preveri

Pravilno

Bravo. Na vsa vprašanja si odgovoril pravilno.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Preberi si rešitev.
Rešitev:

a) $\alpha = 65°$ , $\beta = 65°$ in $\gamma = 50°$

b) Enakokraki trikotniki so: $ABC$ , $SBD$ in $CSD$ .

c) Da bi bil trikotnik $ABC$ enakostraničen, bi moral kot $\angle SDC$ meriti $120°$ .

Naloga 5

Konstruiraj trikotnike s podatki:

a) $a=3$ cm, $b=4$ cm in $c=5$ cm

b) $a=5$ cm, $c=3$ cm in $\alpha = 120°$

c) $\alpha′ = 120°$ , $a=6$ cm in $c=5$ cm

Trikotnik

Vaš brskalnik je zastarel

Pritisnite F11

Trikotnik

Avtor: E-um (vsebinsko), Skupina NAUK (tehnično)

Sodelujoče organizacije

Hvala za ogled gradiva!

Veseli bomo vaših komentarjev. Obiščite nas na www.nauk.si.

Uporabljeni viri

Sodelujoče organizacije

Pravilno

Napačno

Napačno

Pravilno

Napačno

Napačno

Pravilno

Napačno

Napačno

Pravilno

Napačno

Napačno

Pravilno

Napačno

Napačno

Pravilno

Napačno

Napačno