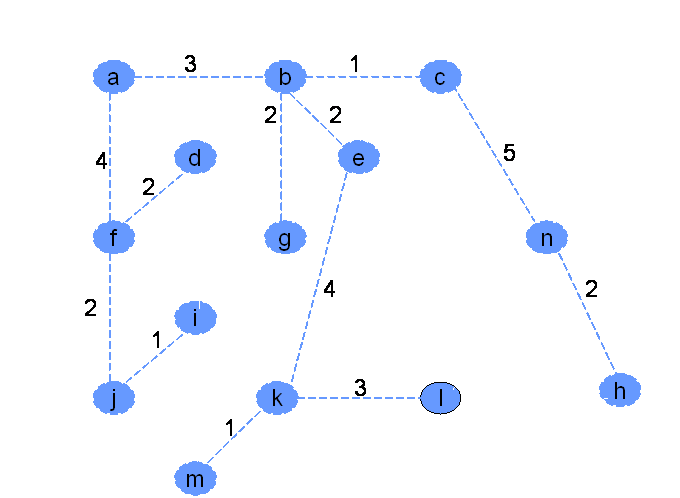
Minimalno vpeto drevo - zgled 1
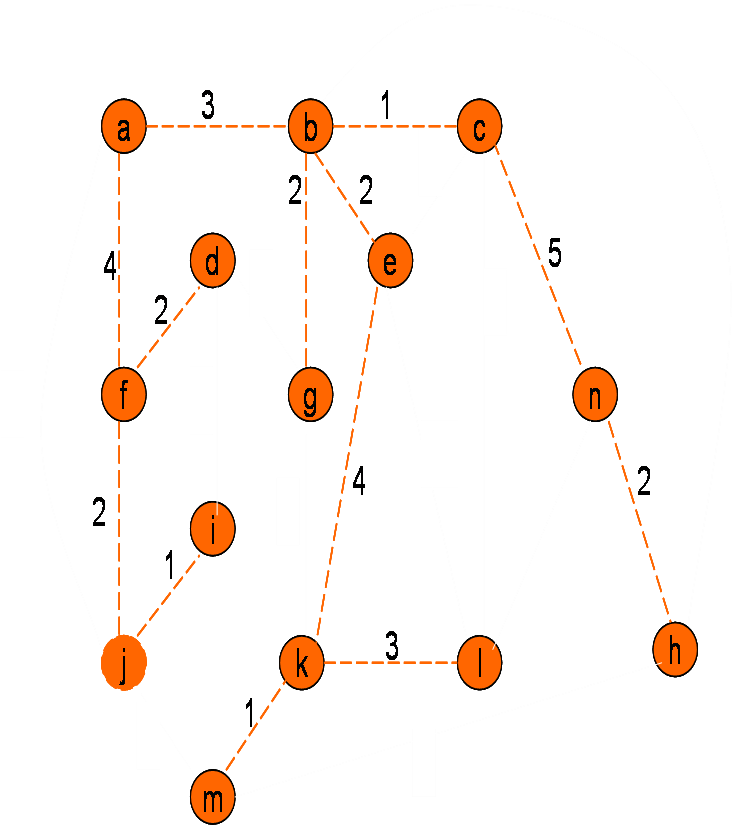
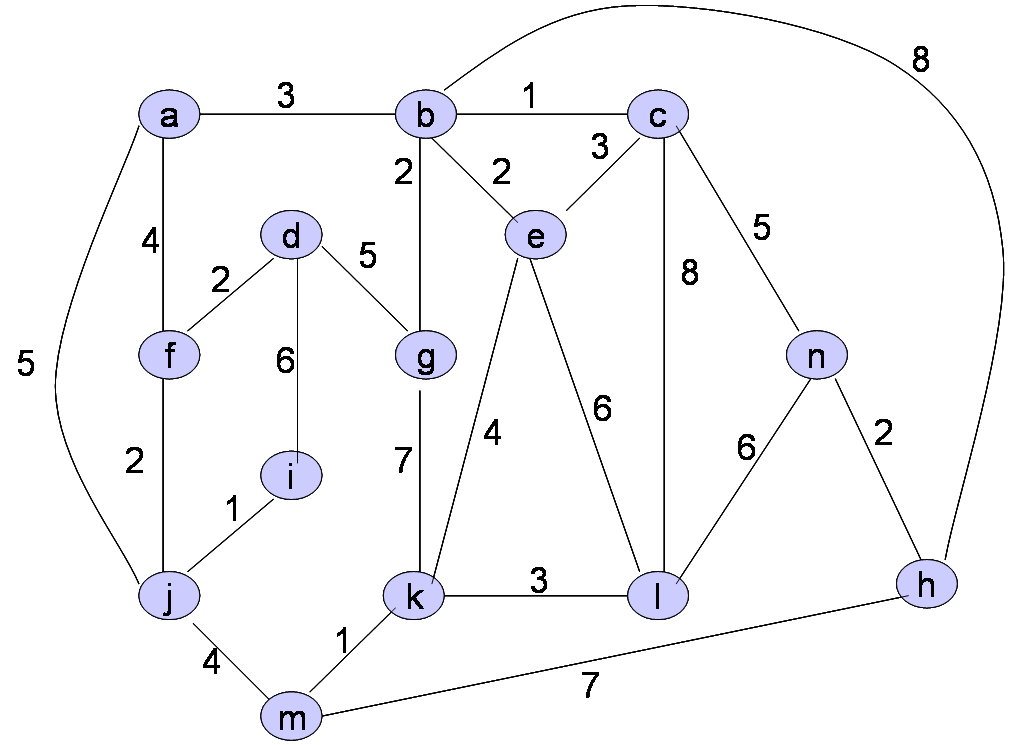
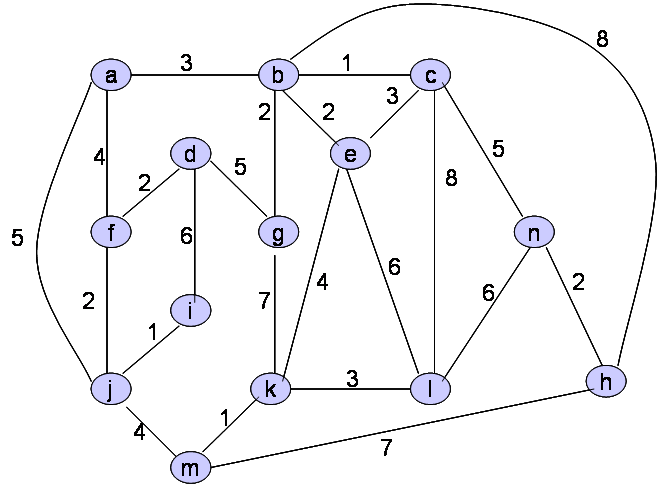
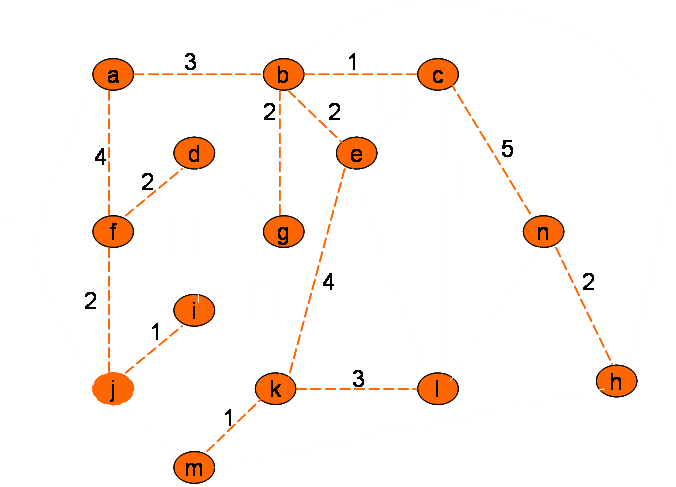
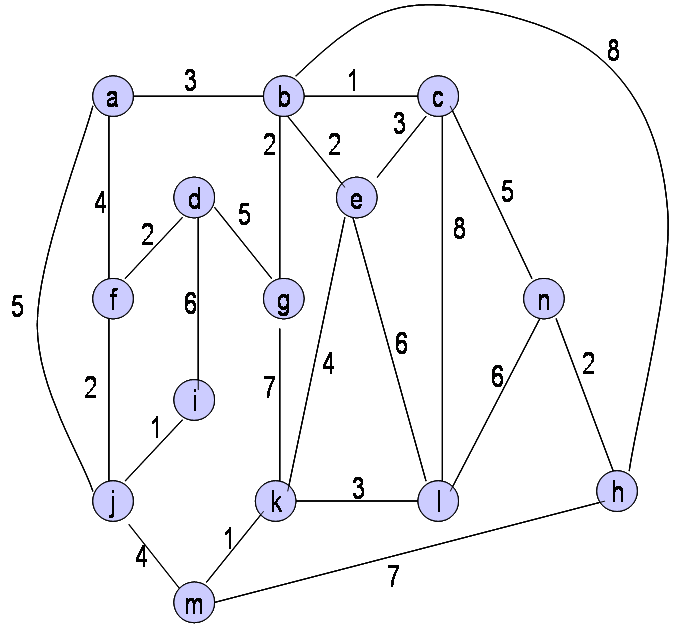
Omrežje

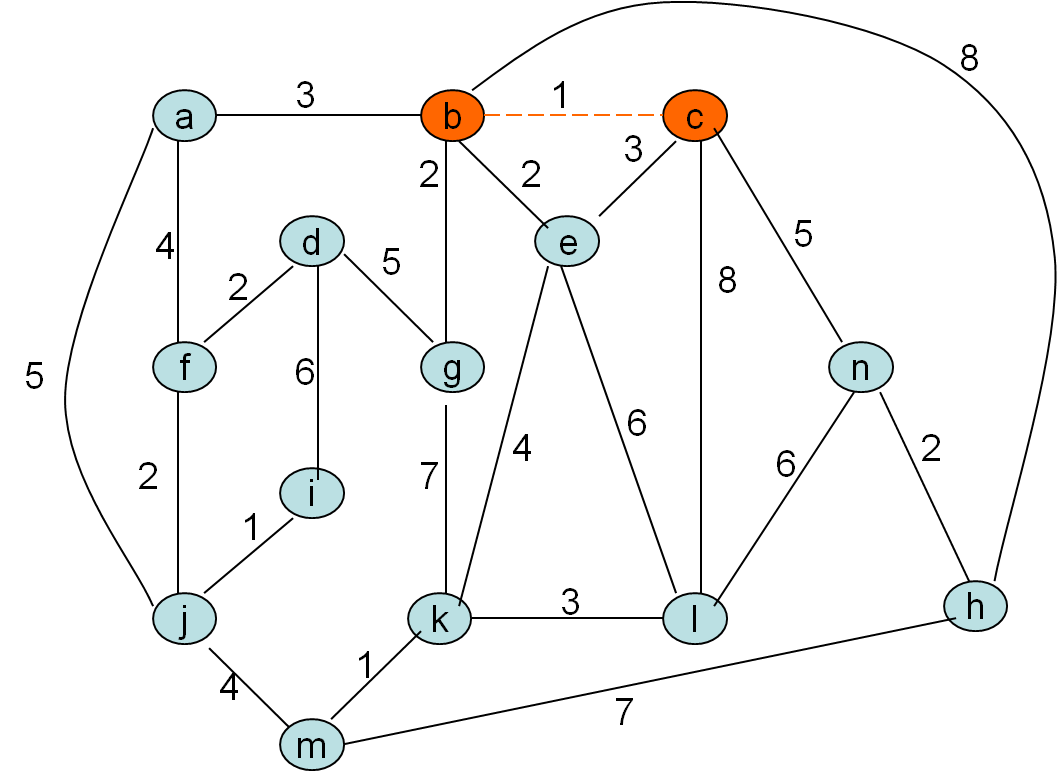
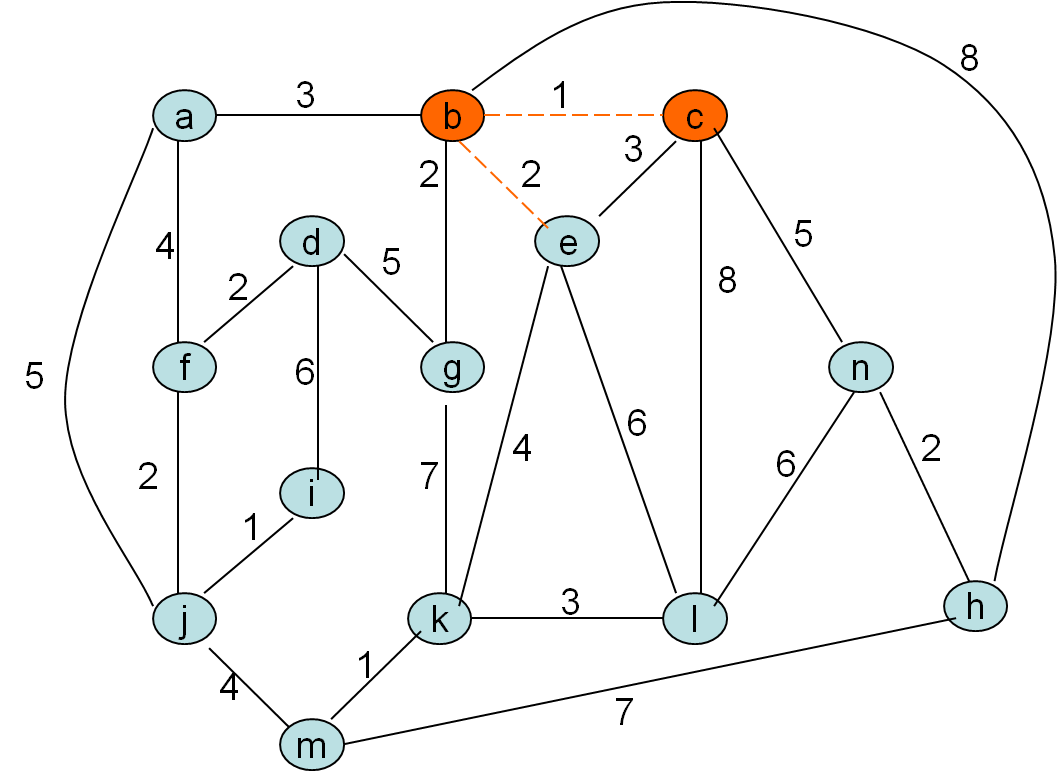
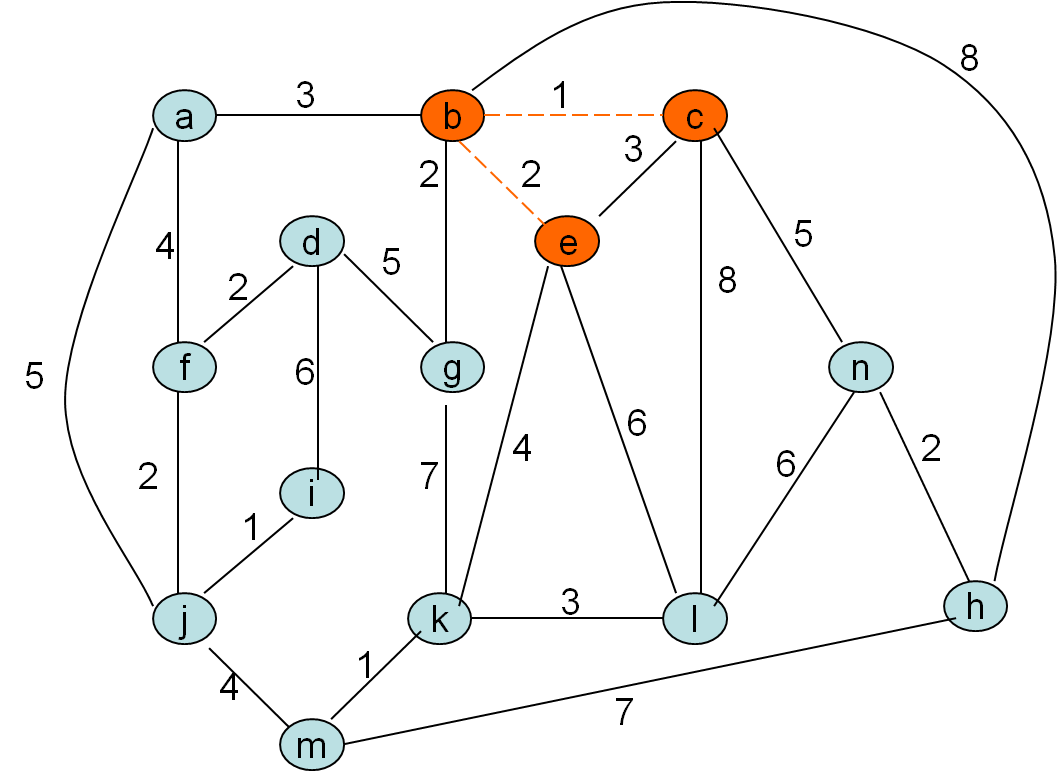
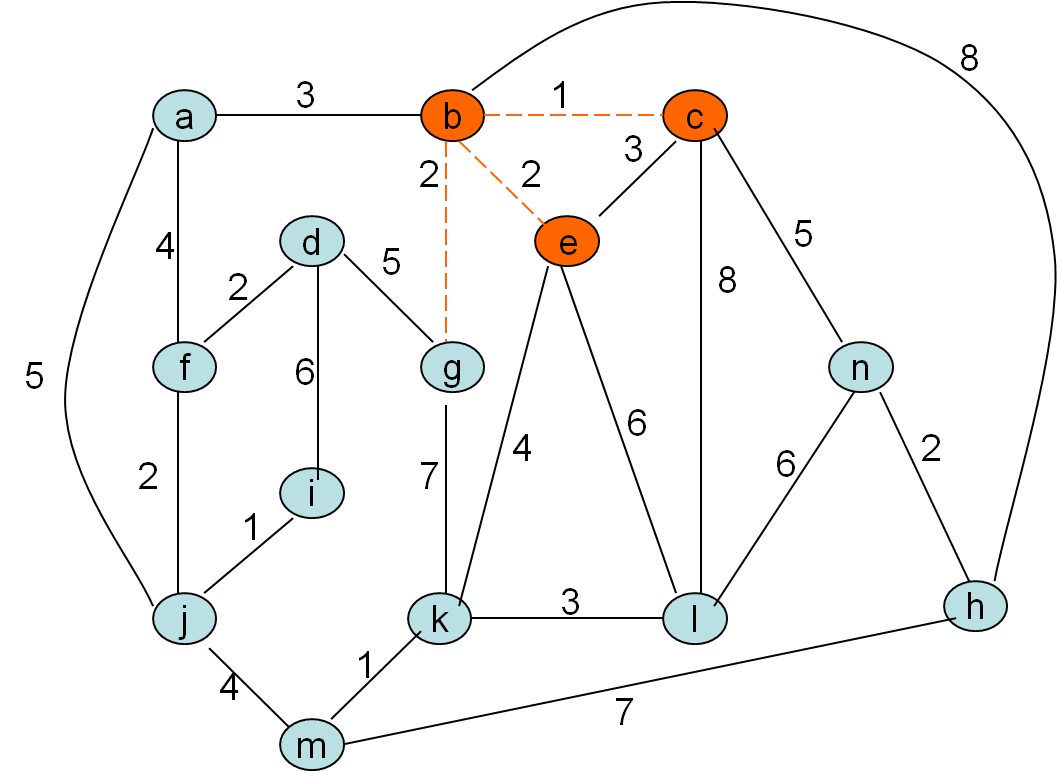
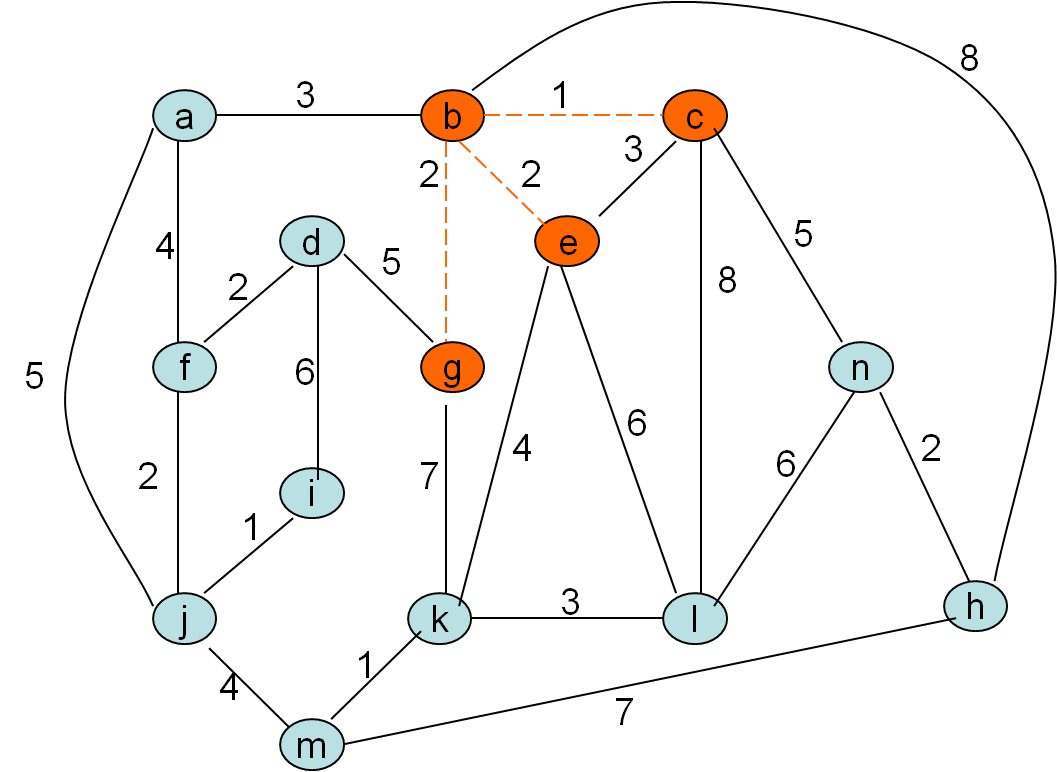
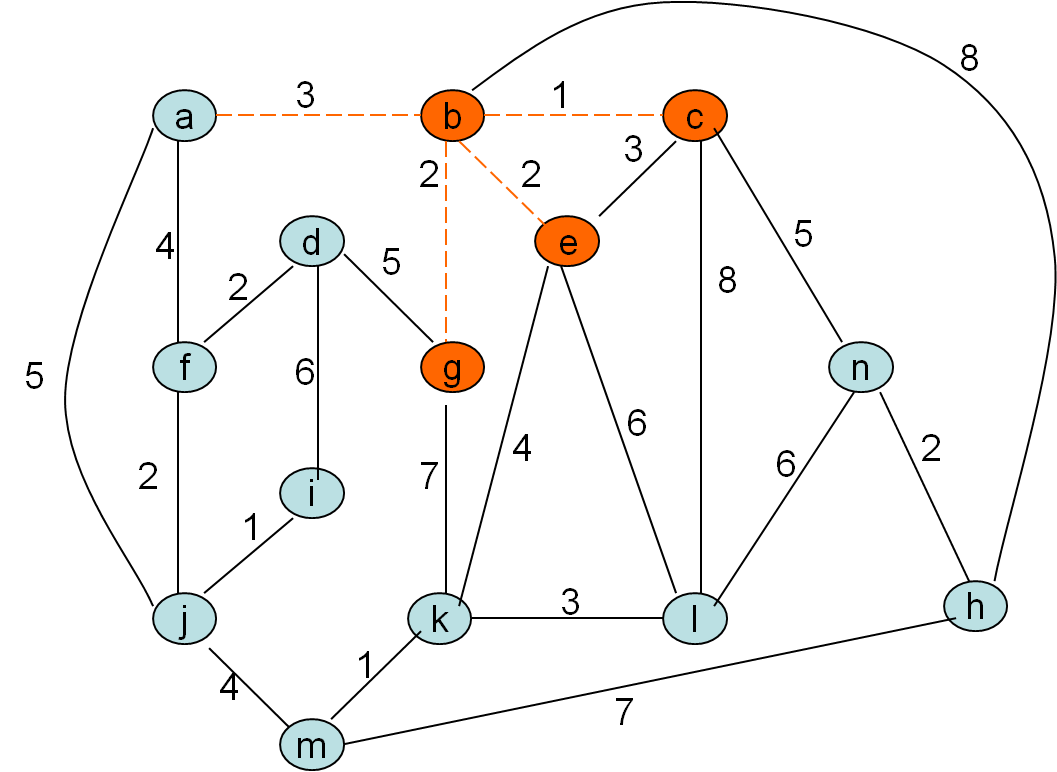
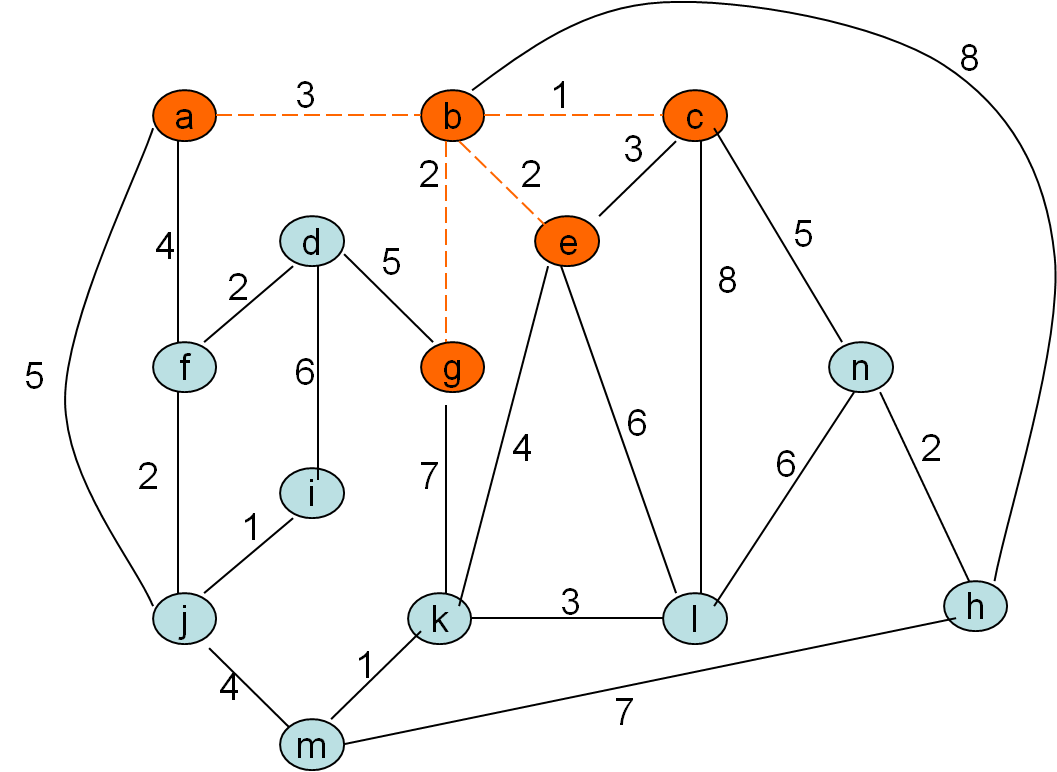
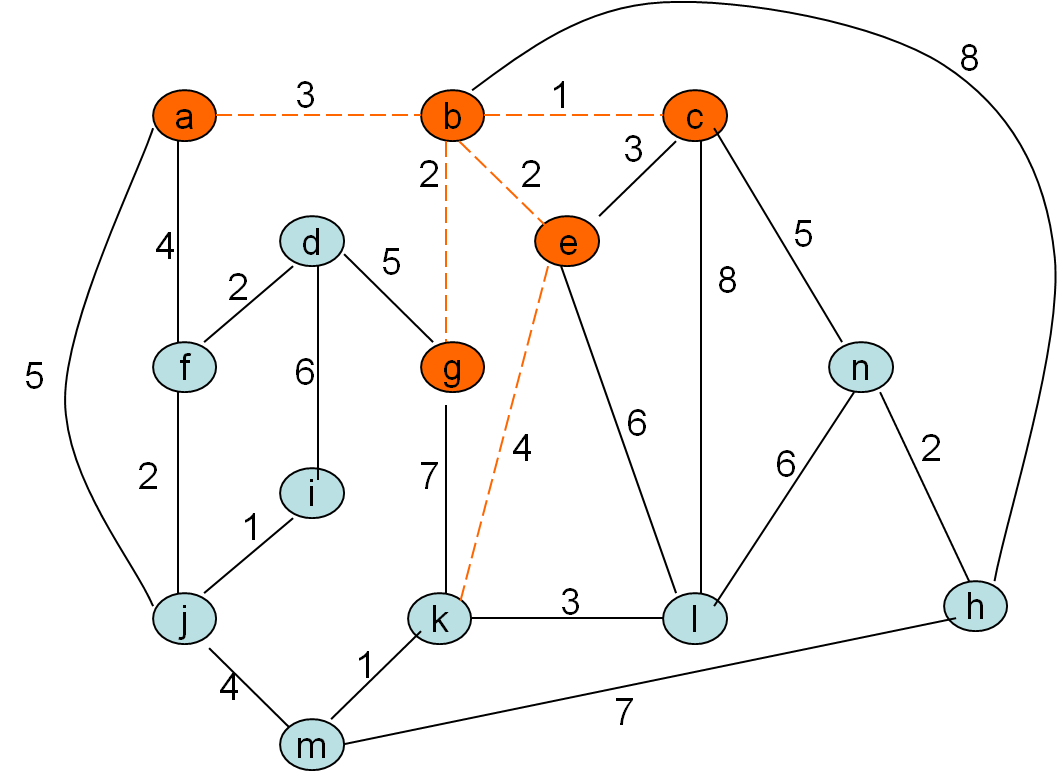
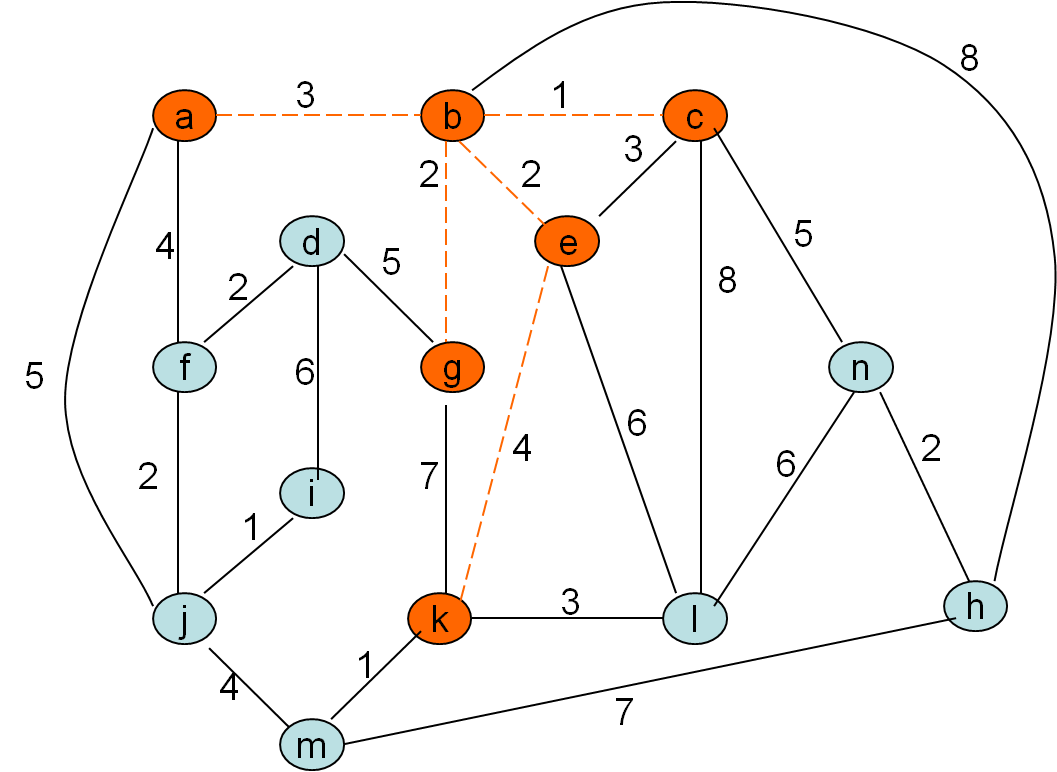
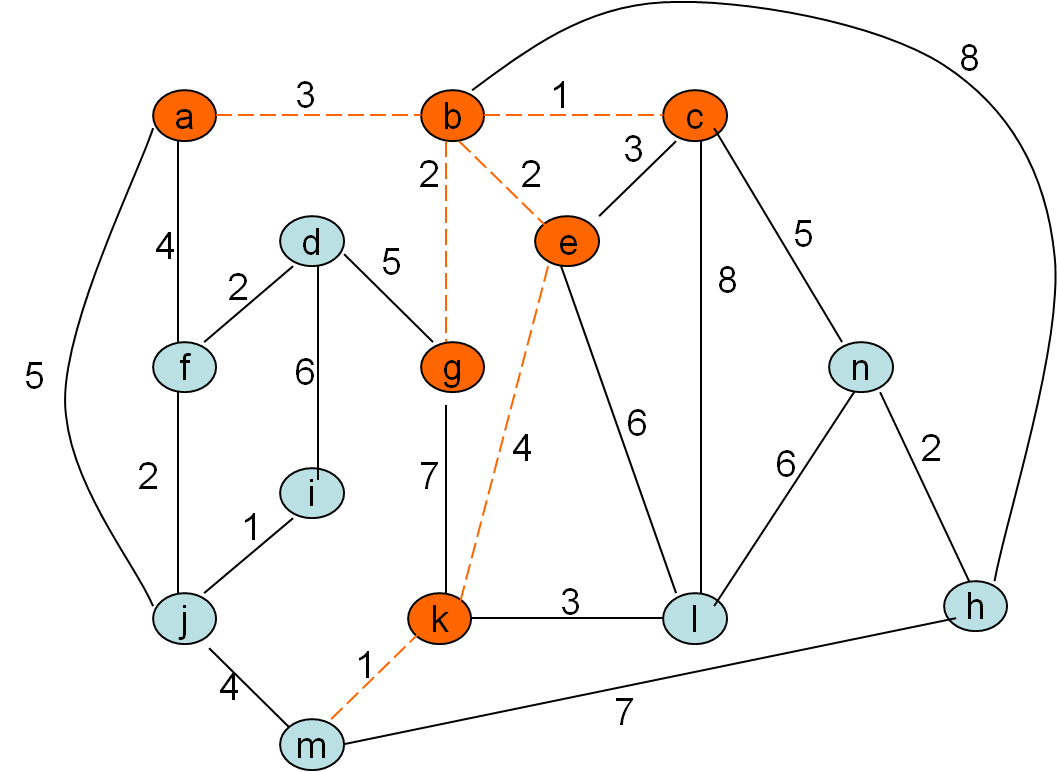
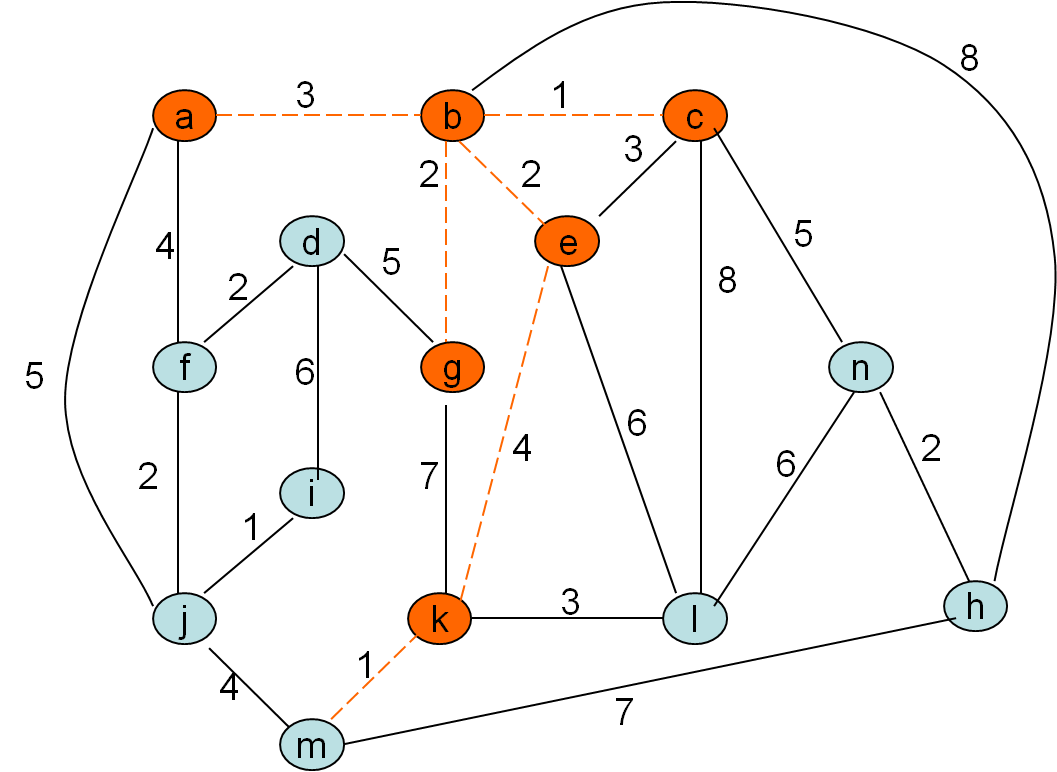
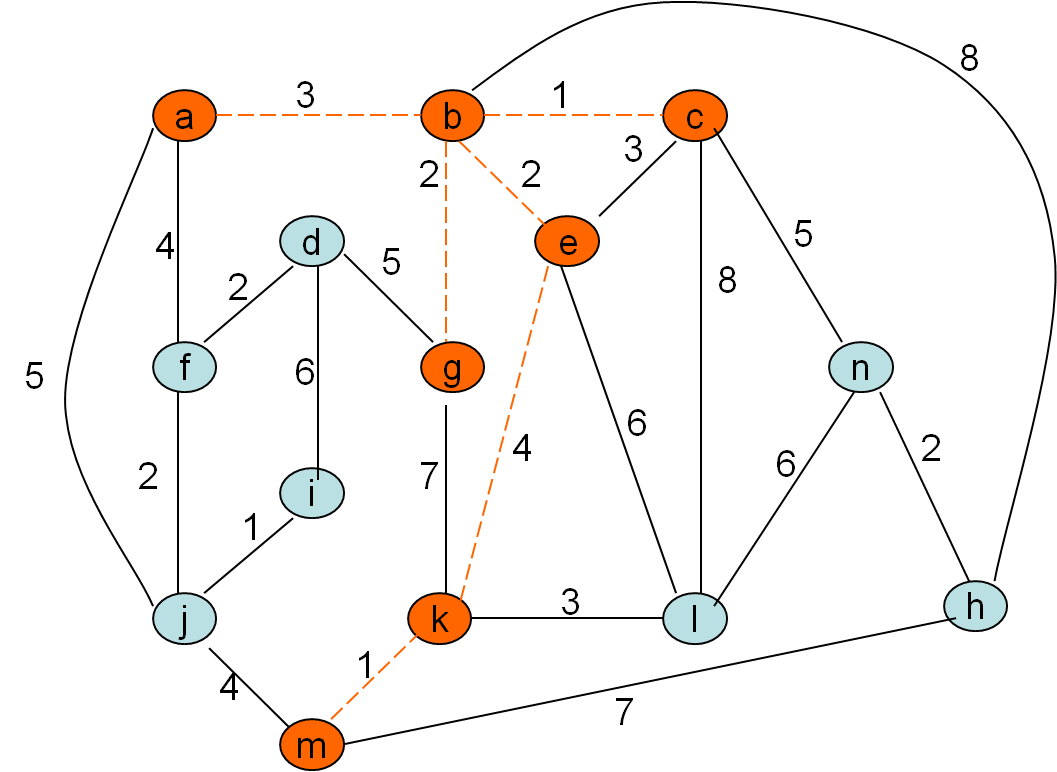
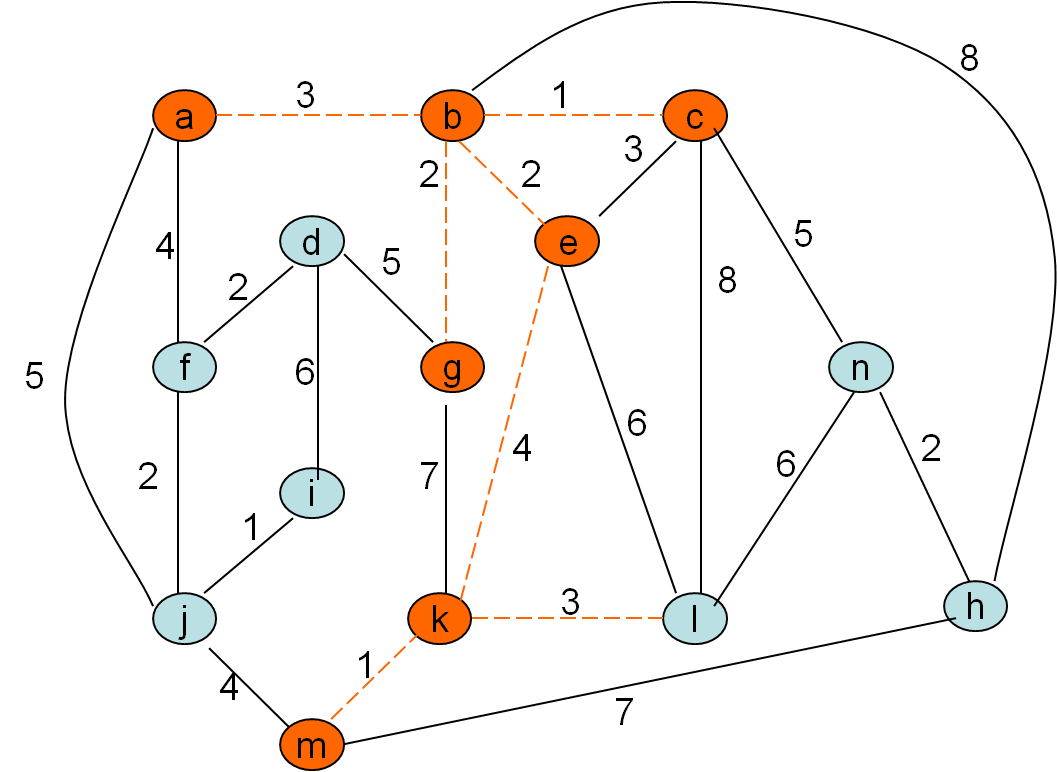
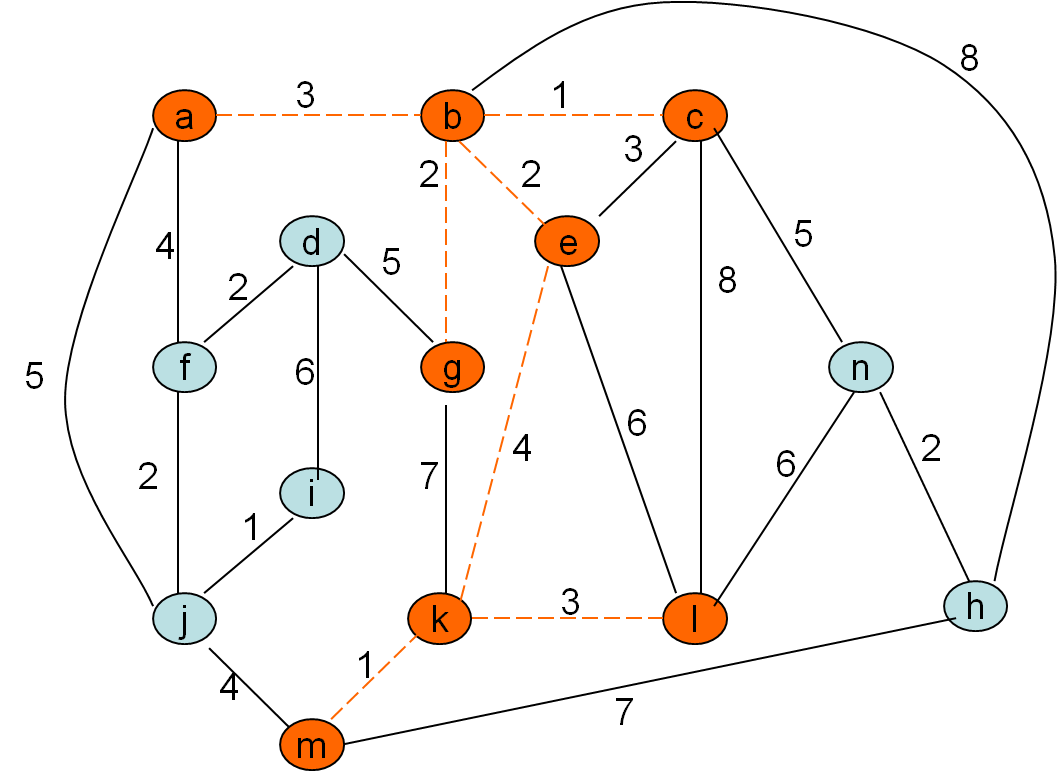
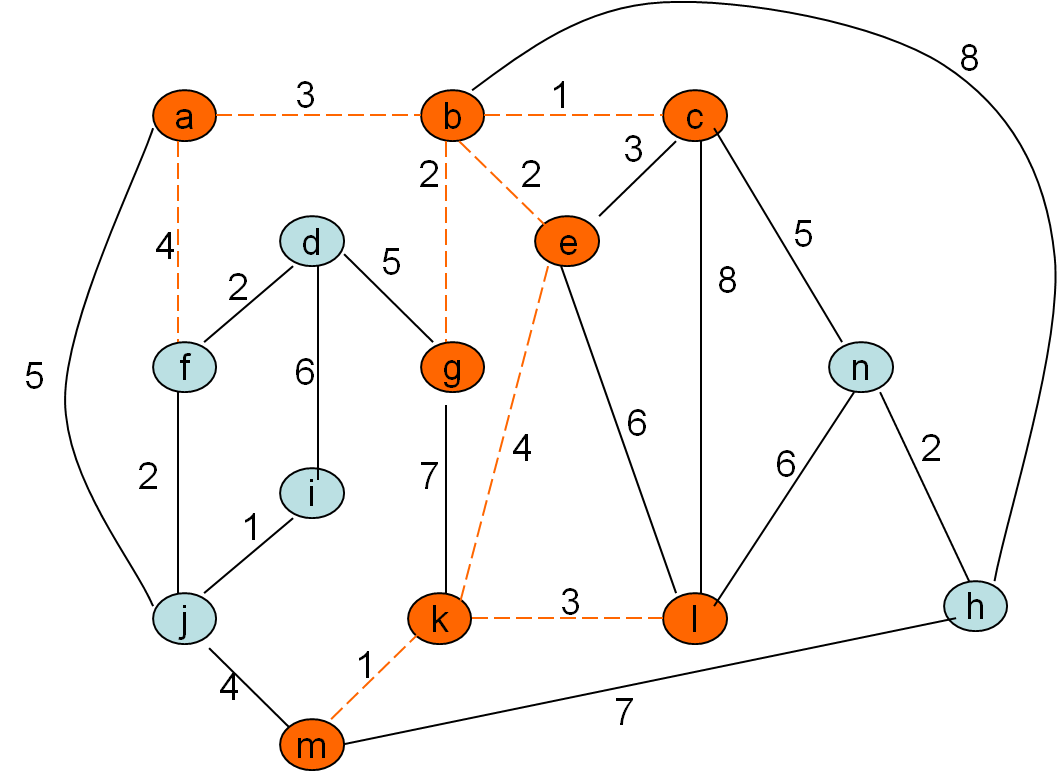
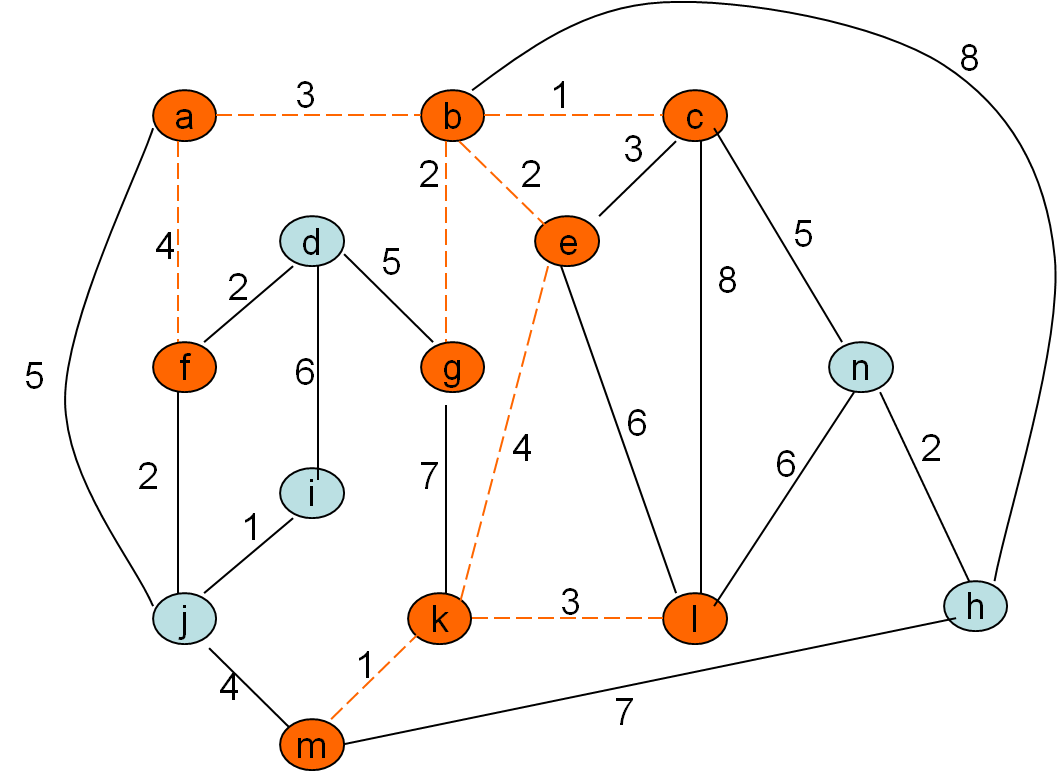
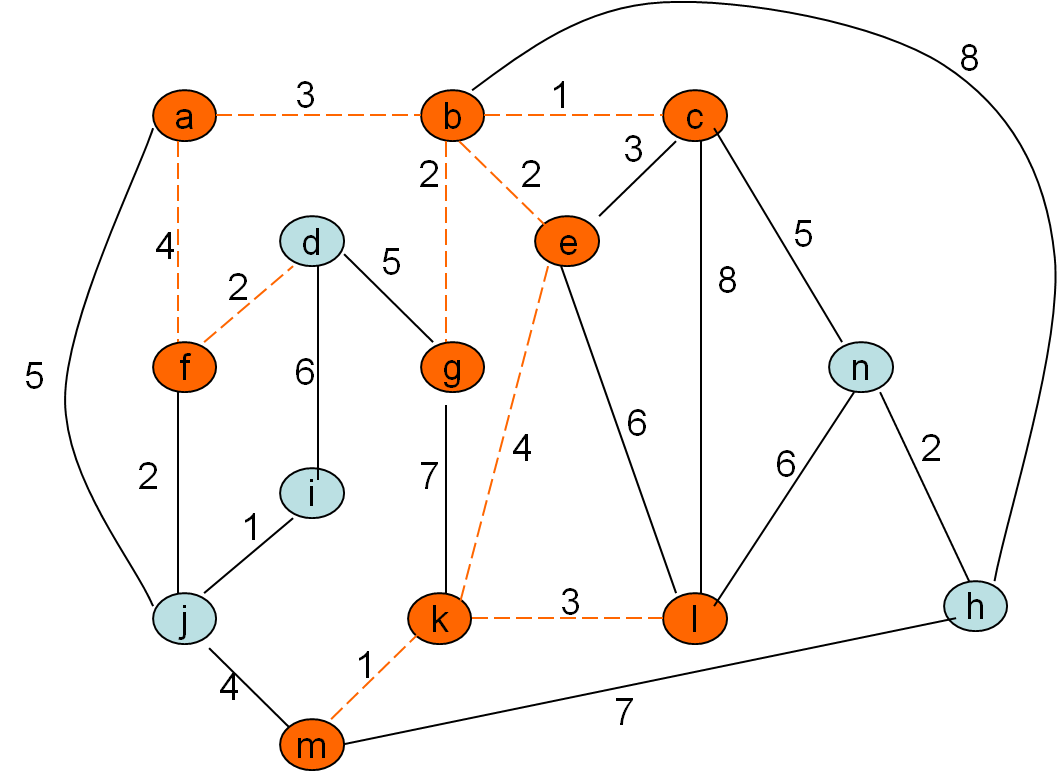
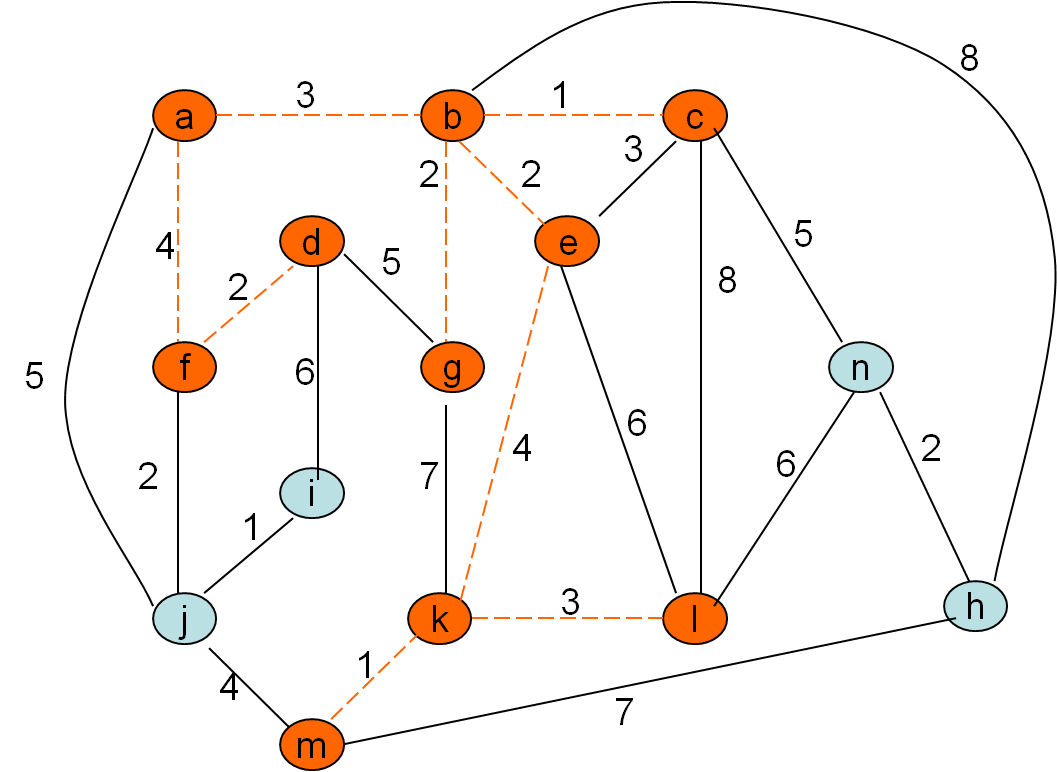
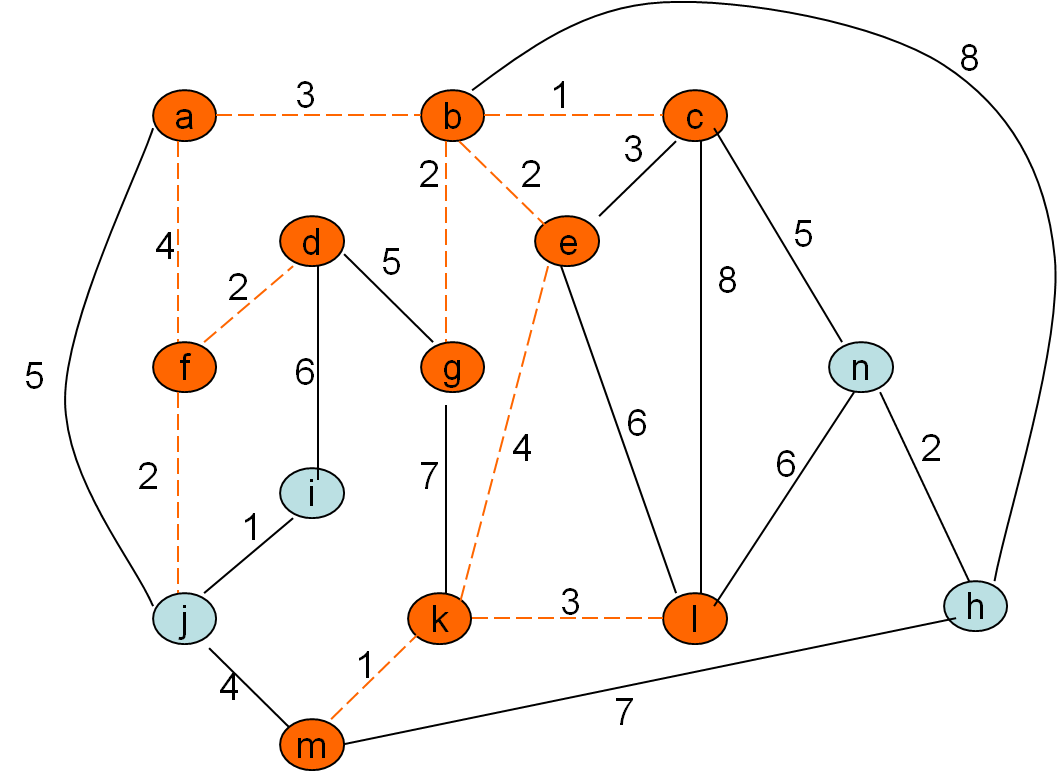
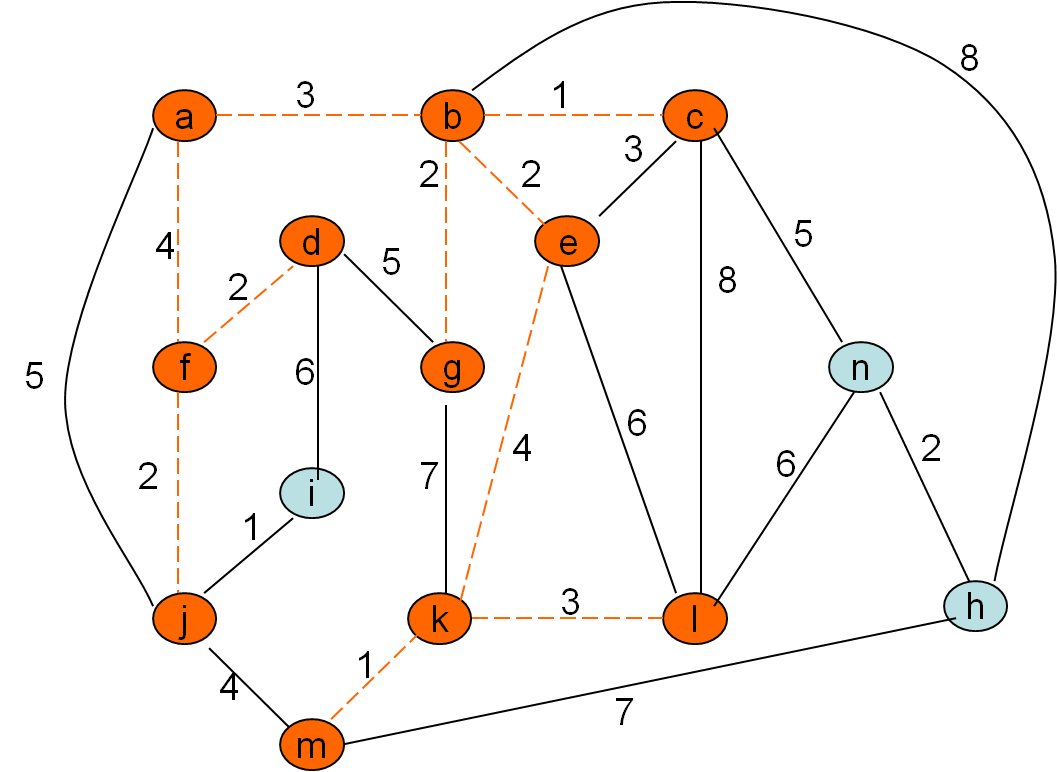
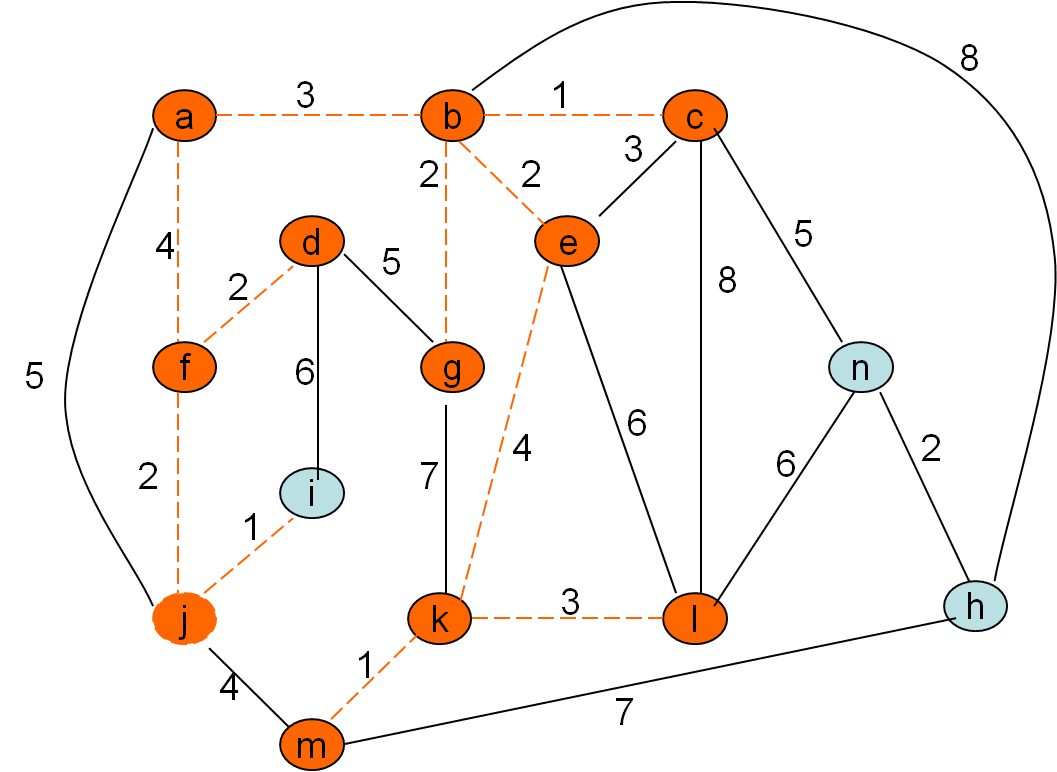
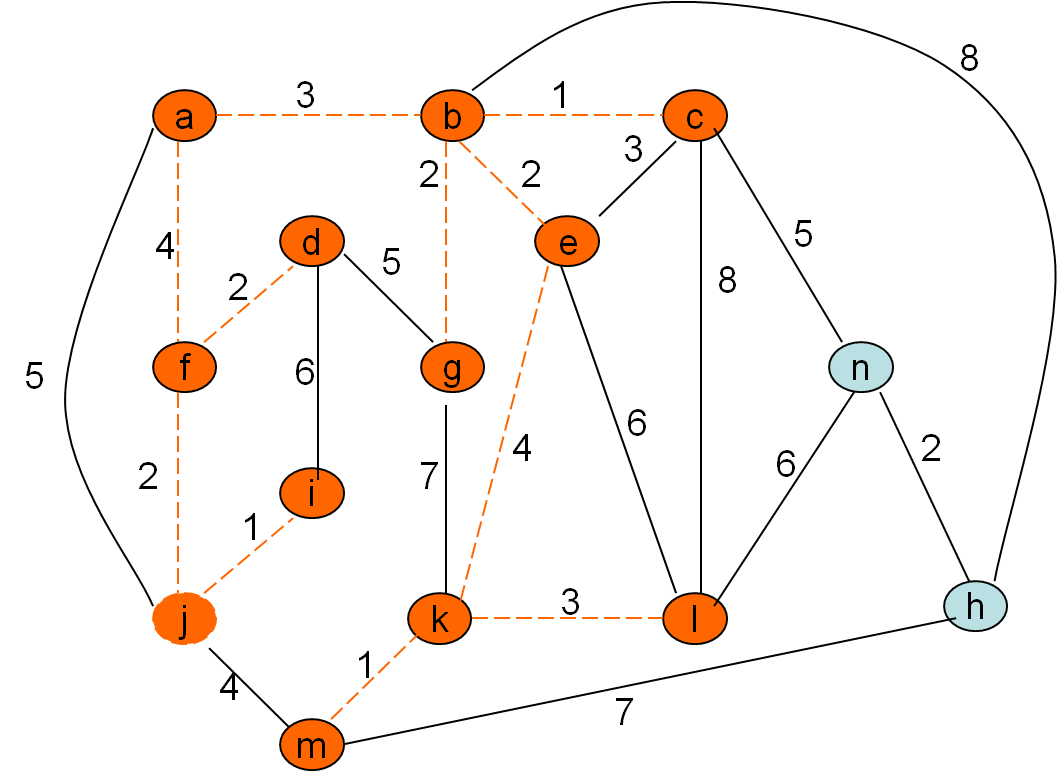
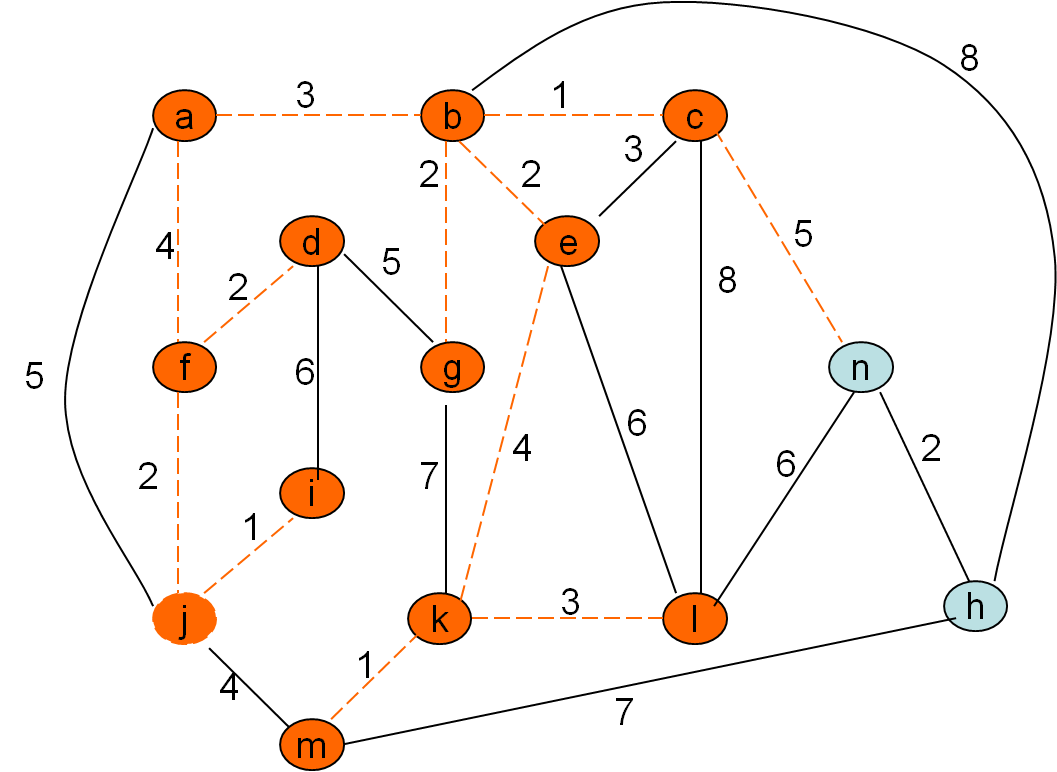
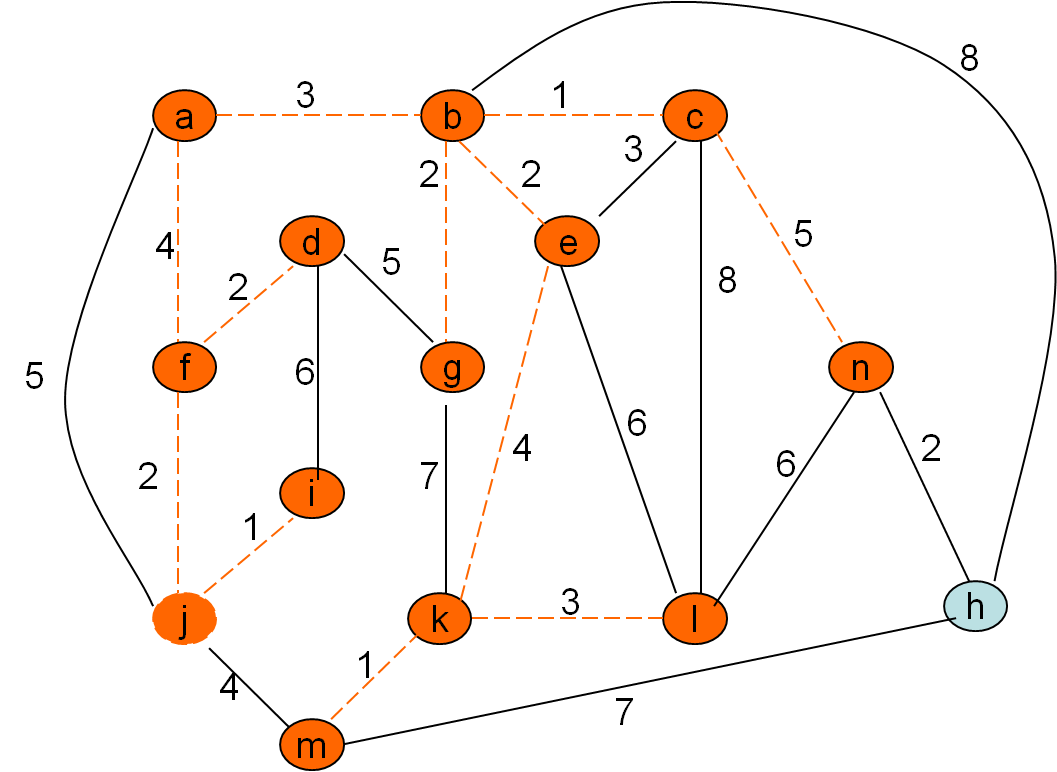
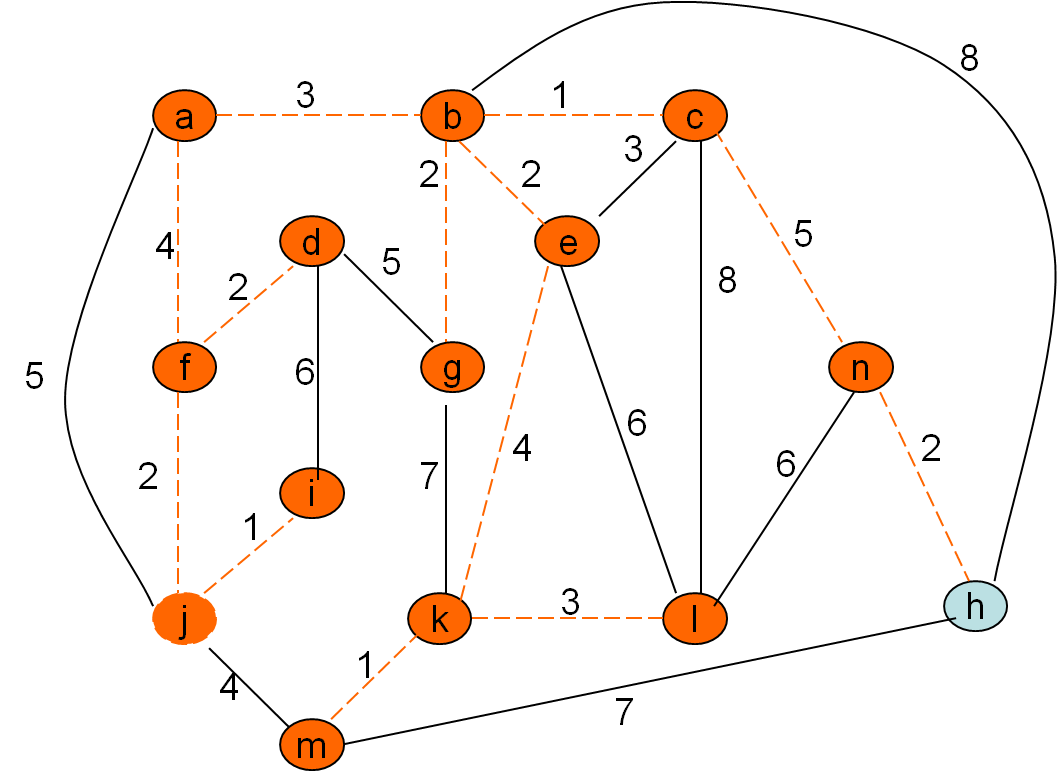
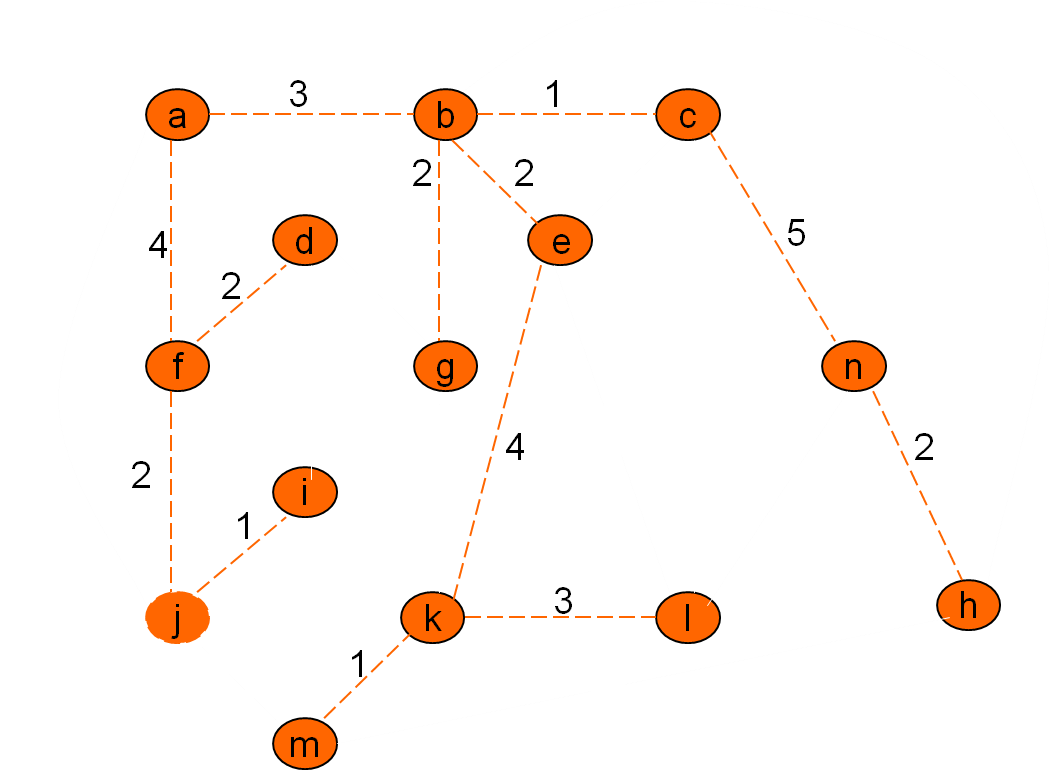
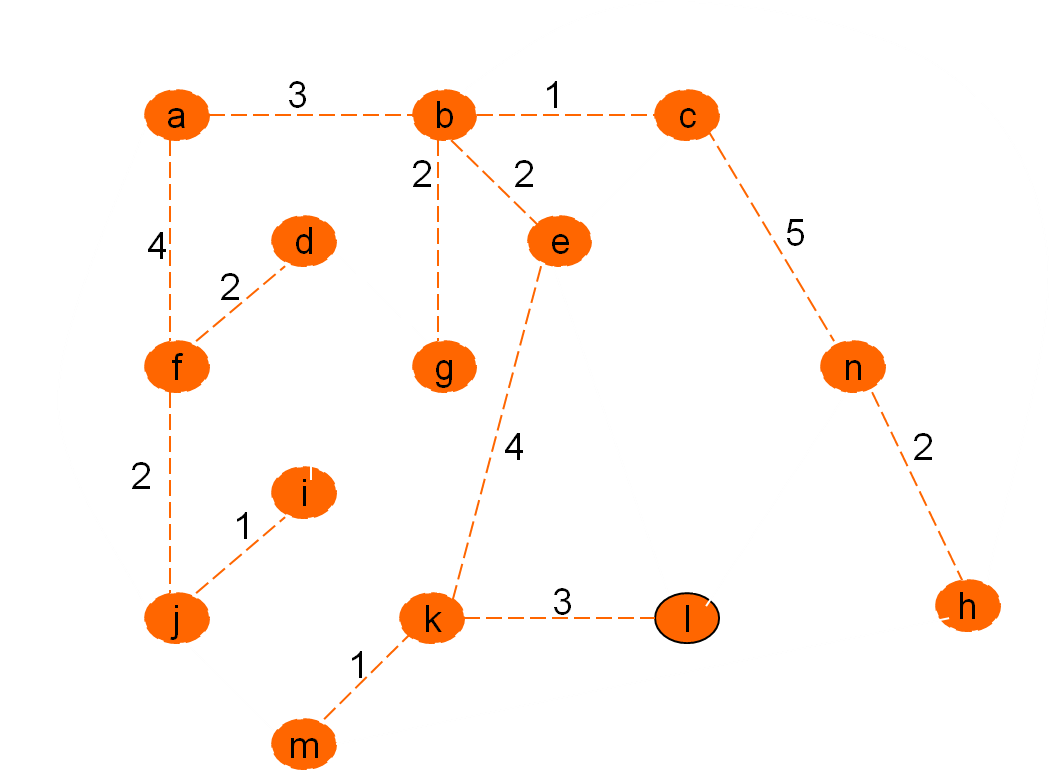
Minimalno vpeto drevo po Primovem postopku
| 
|
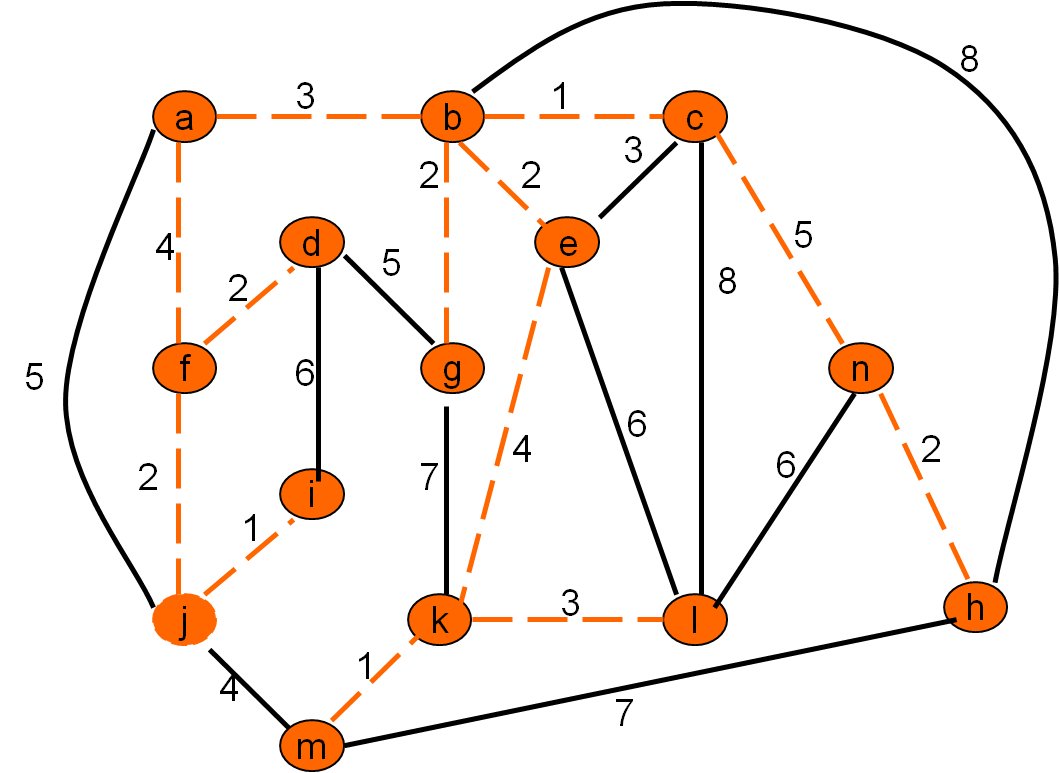
Cena grafa: 32
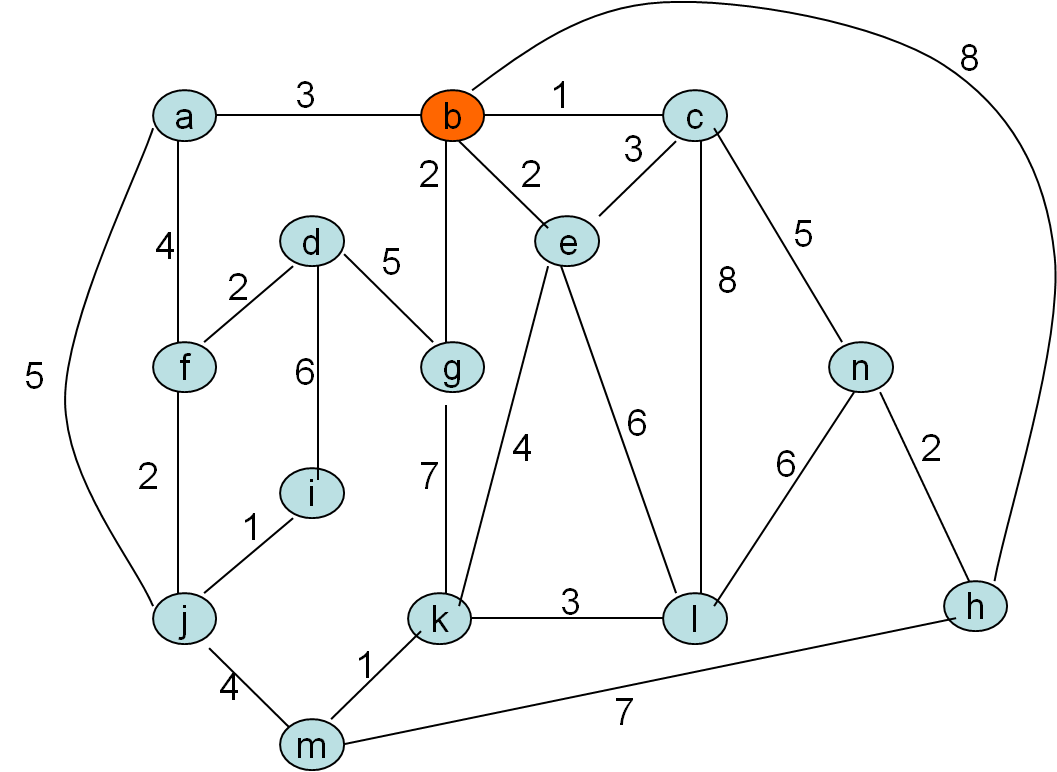
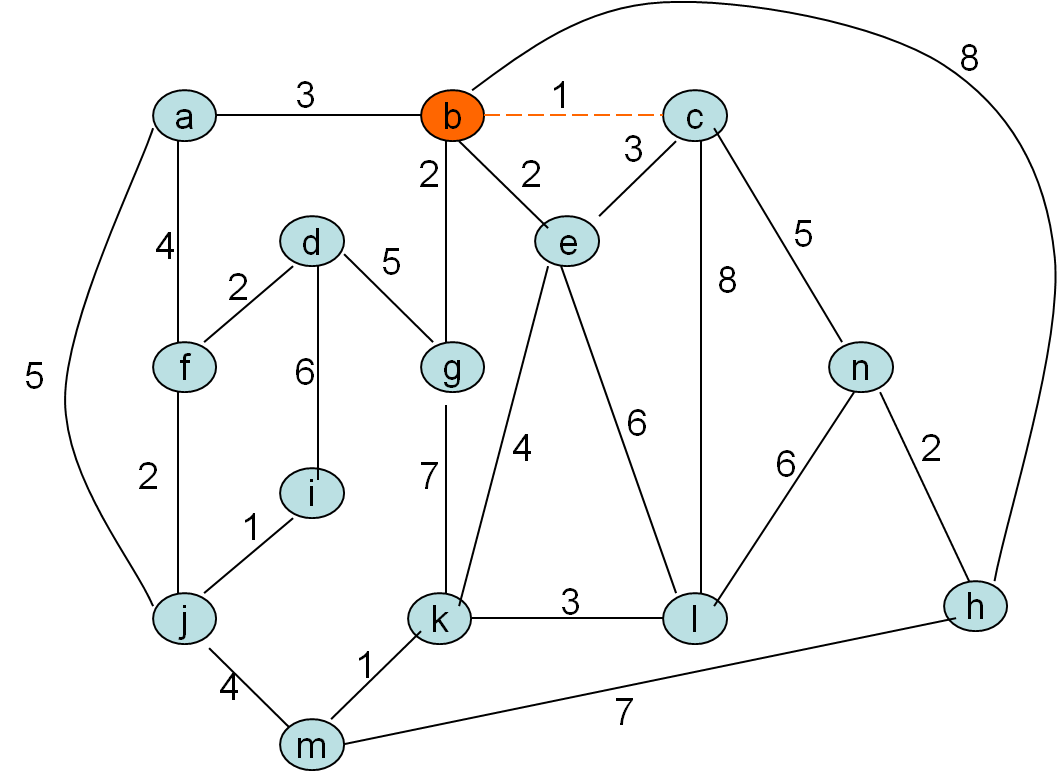
Kurskalov algoritem
Po privzetku gradimo gozd in tekočo najcenejšo povezavo privzamemo, če ne naredi cikla. To pa bo natanko tedaj, ko nista obe vozlišči povezave (u,v) v istem drevesu, v isti (disjunktni) komponenti
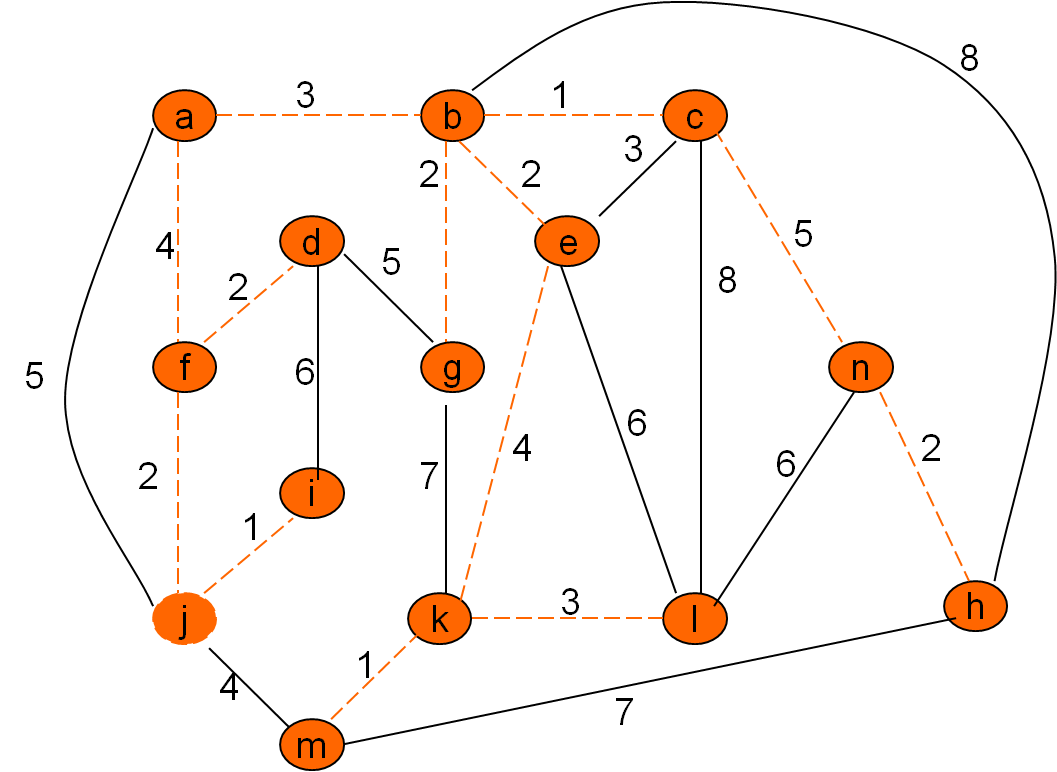
Omrežje
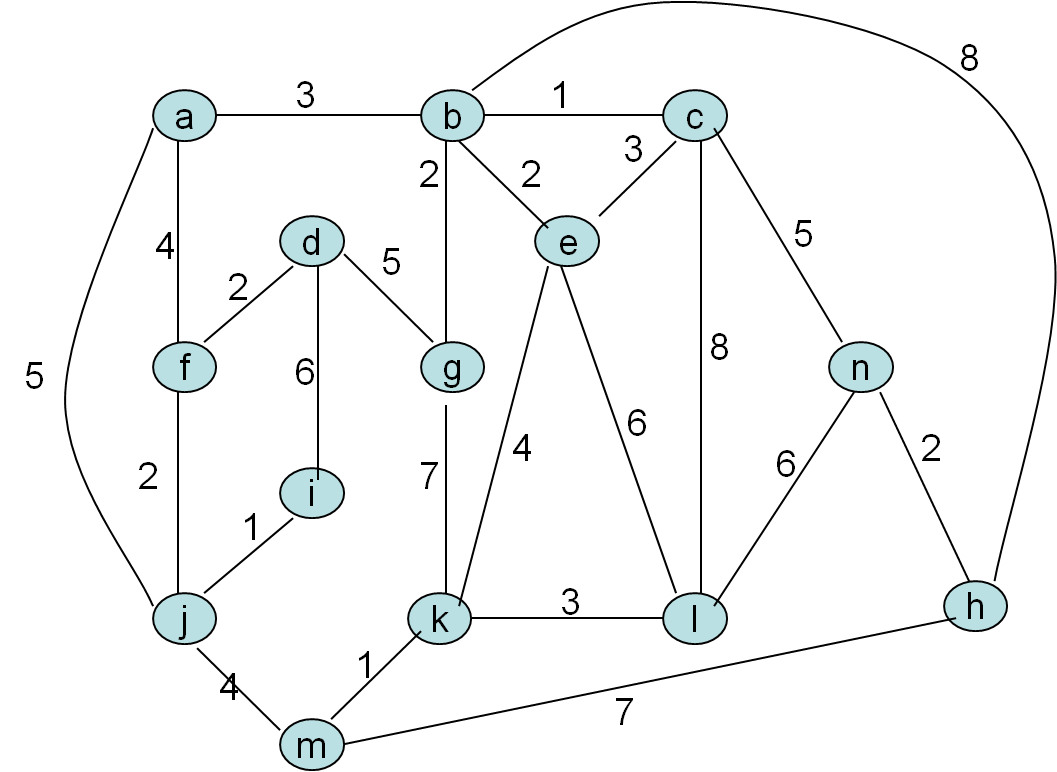
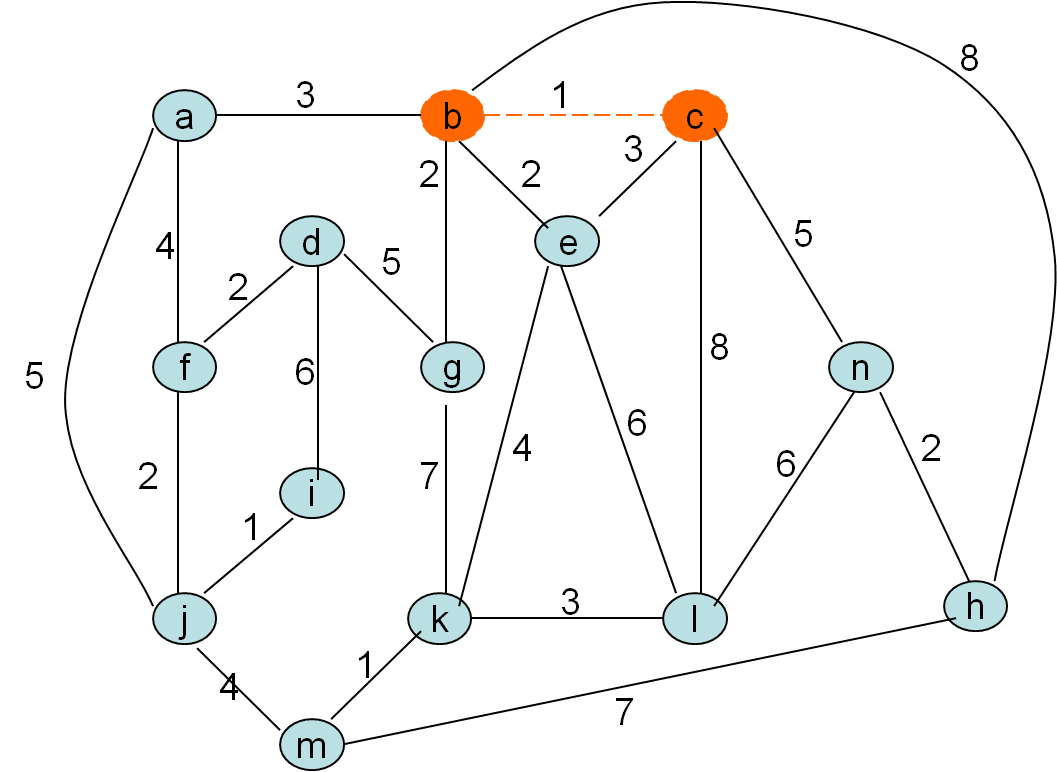
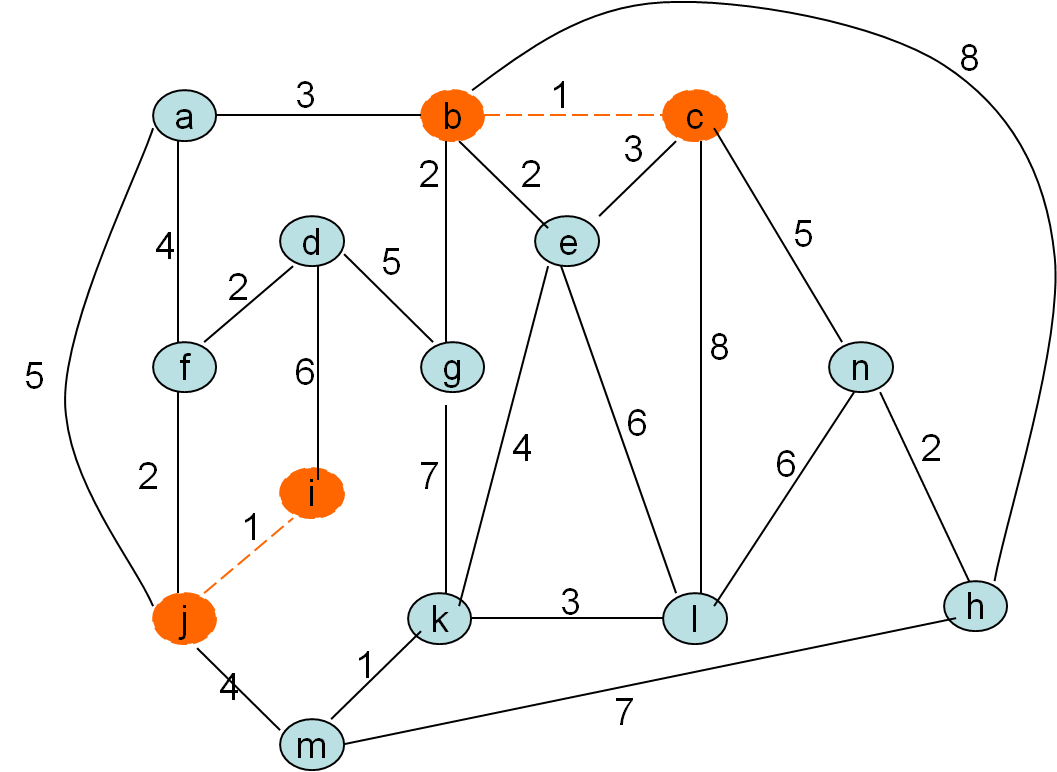
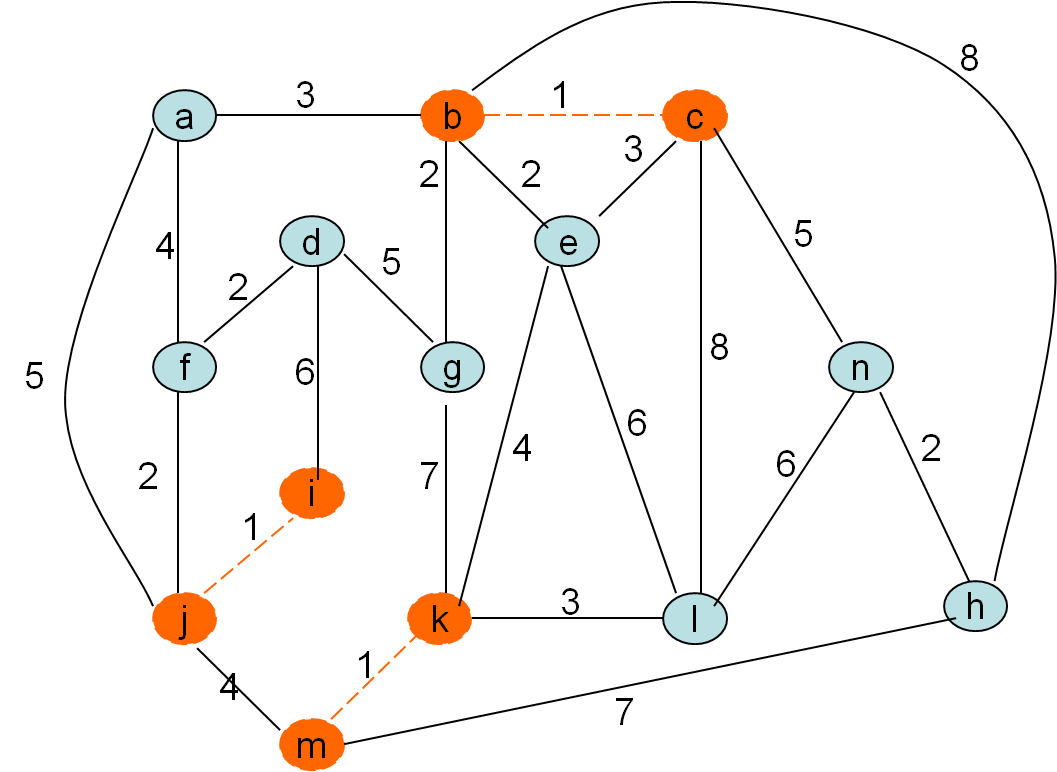
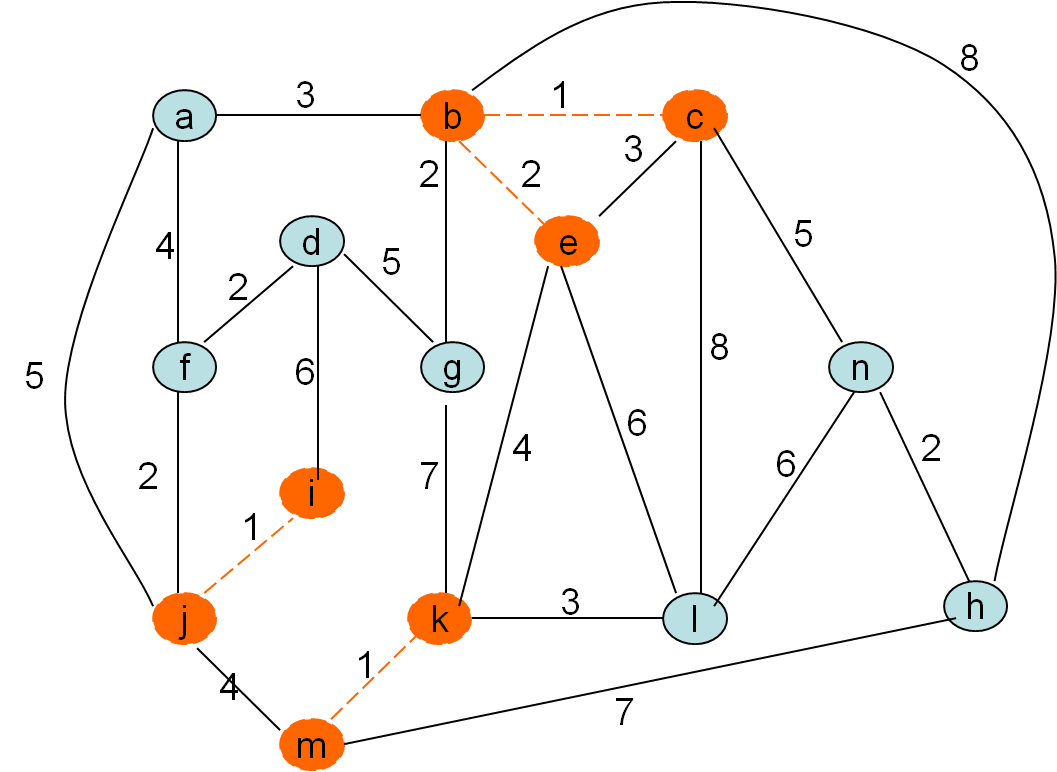
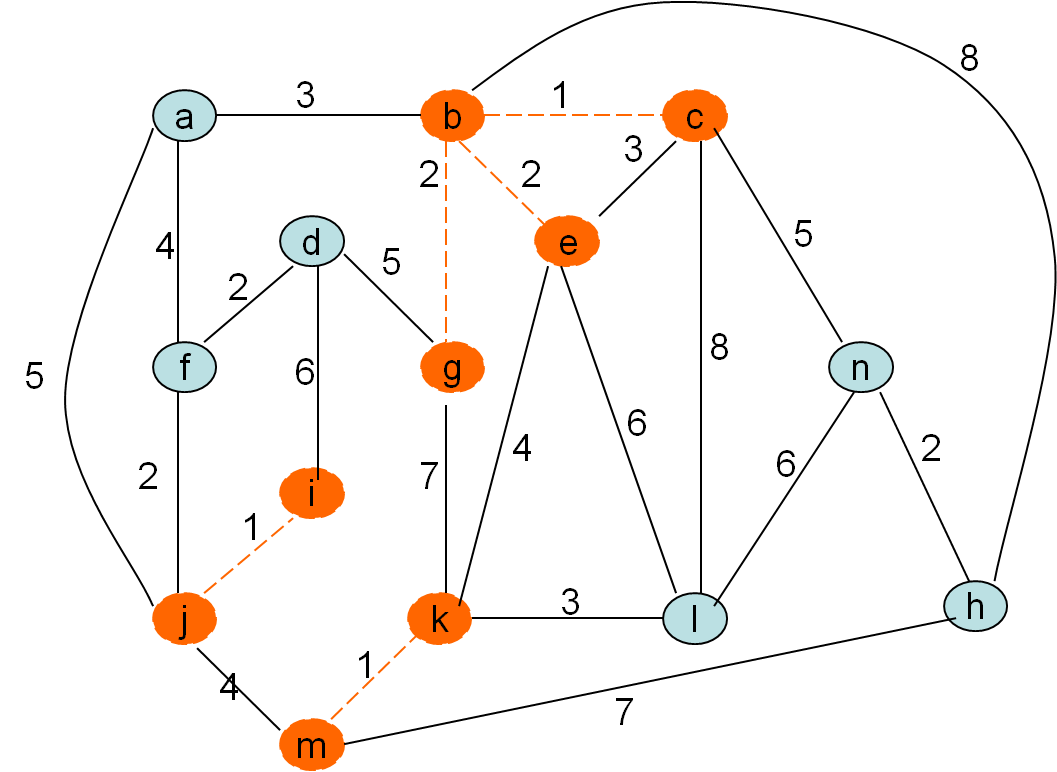
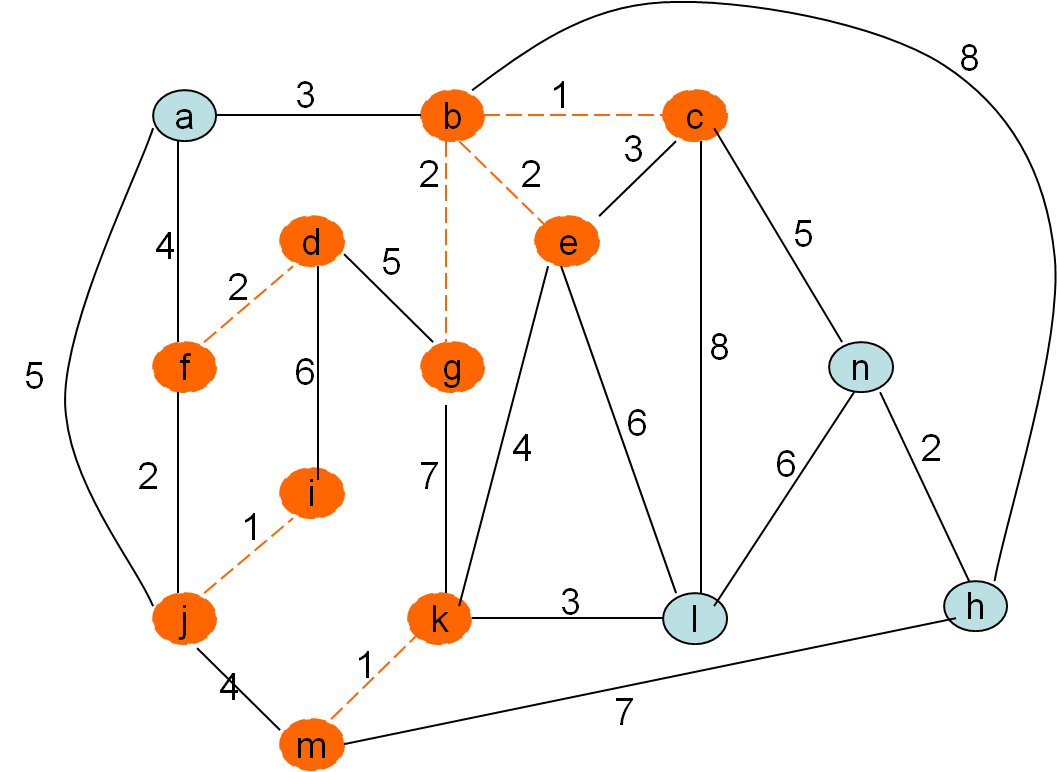
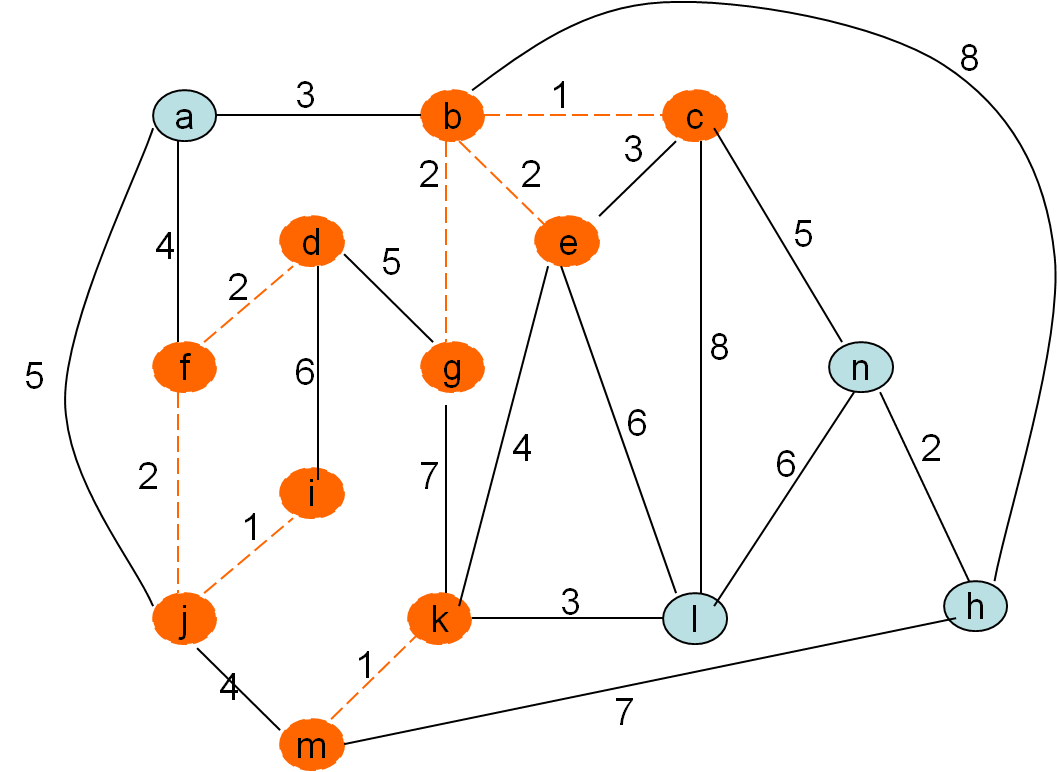
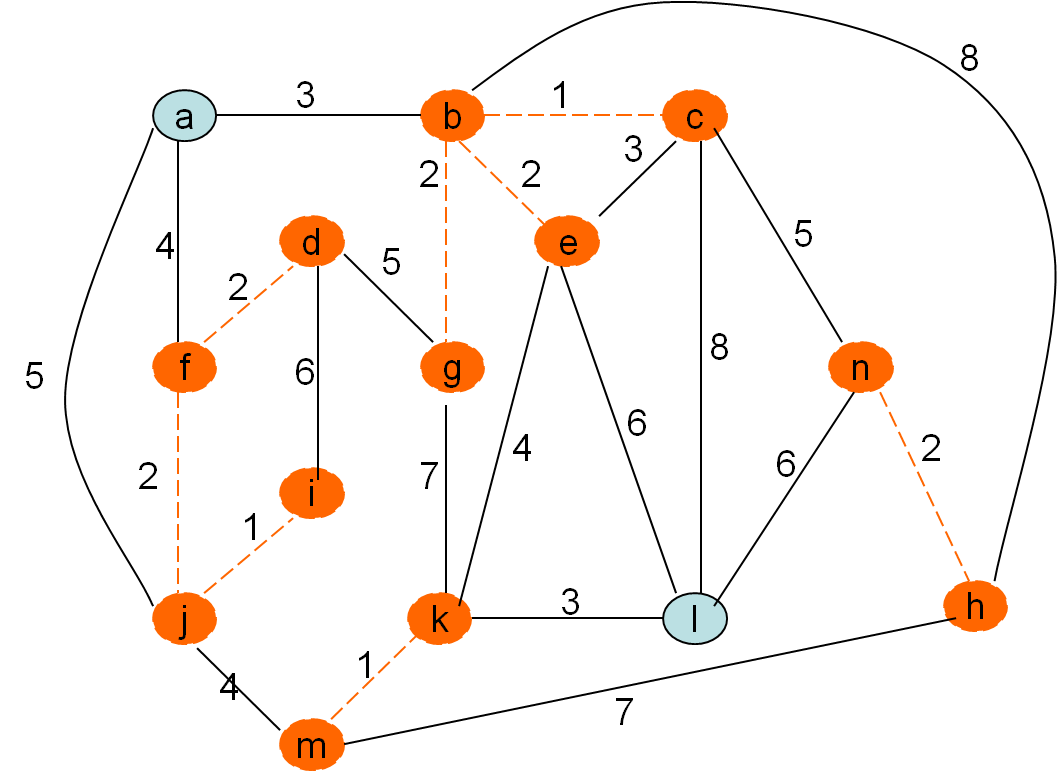
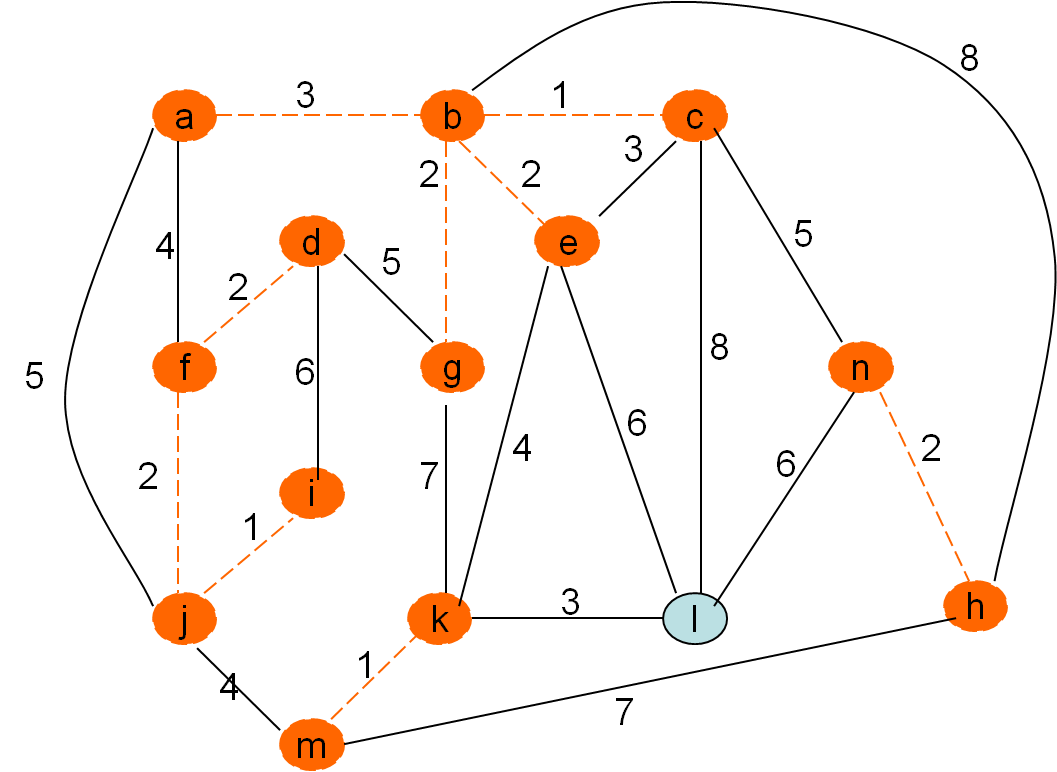
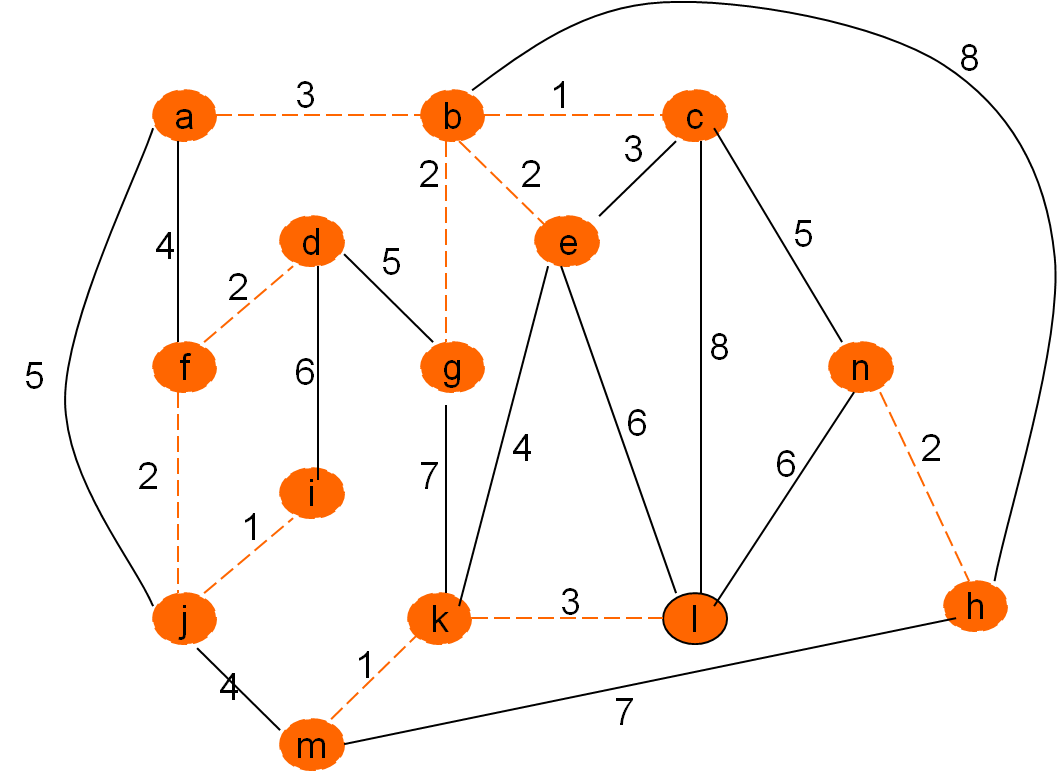
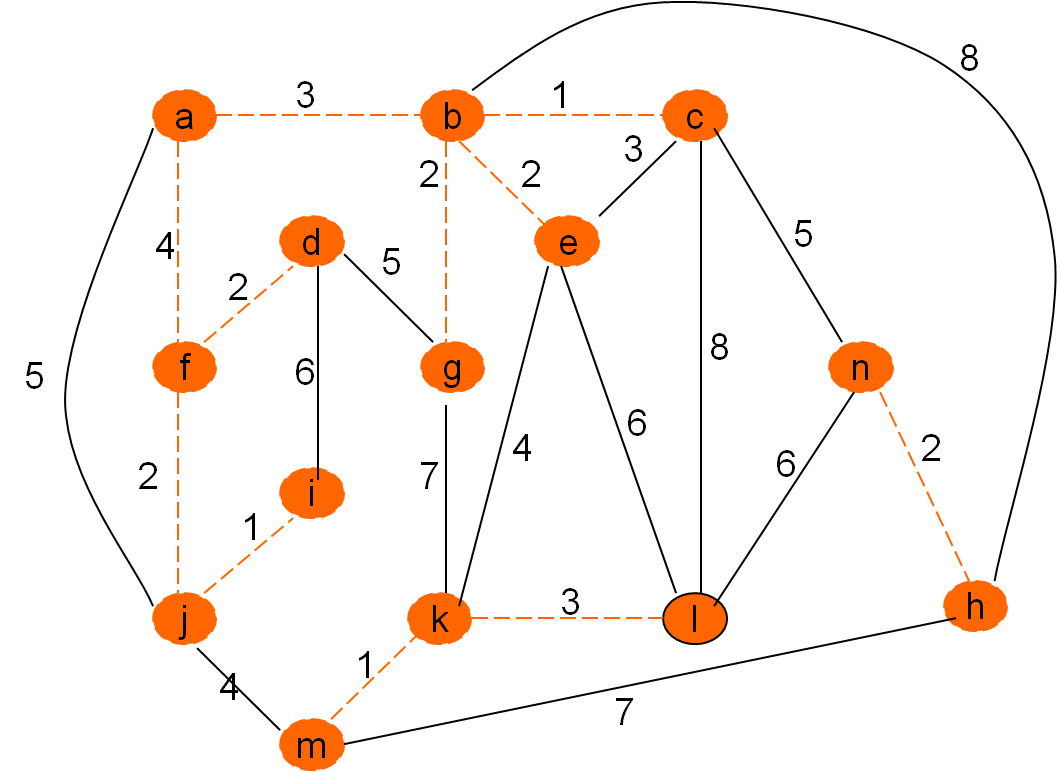
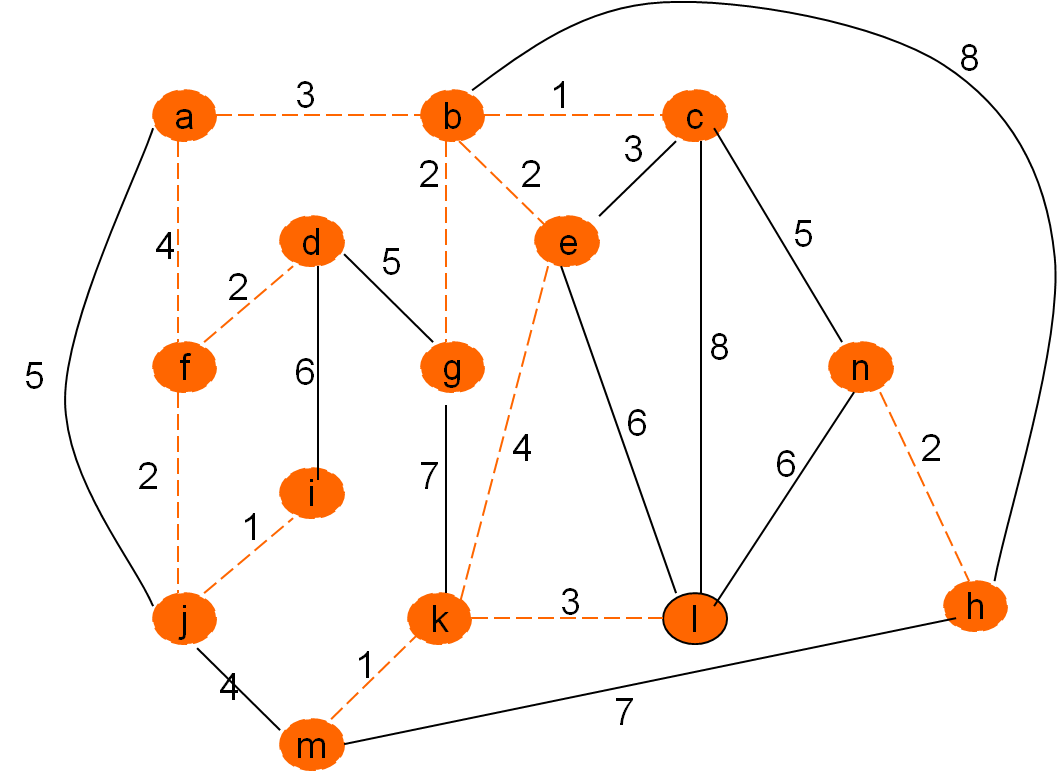
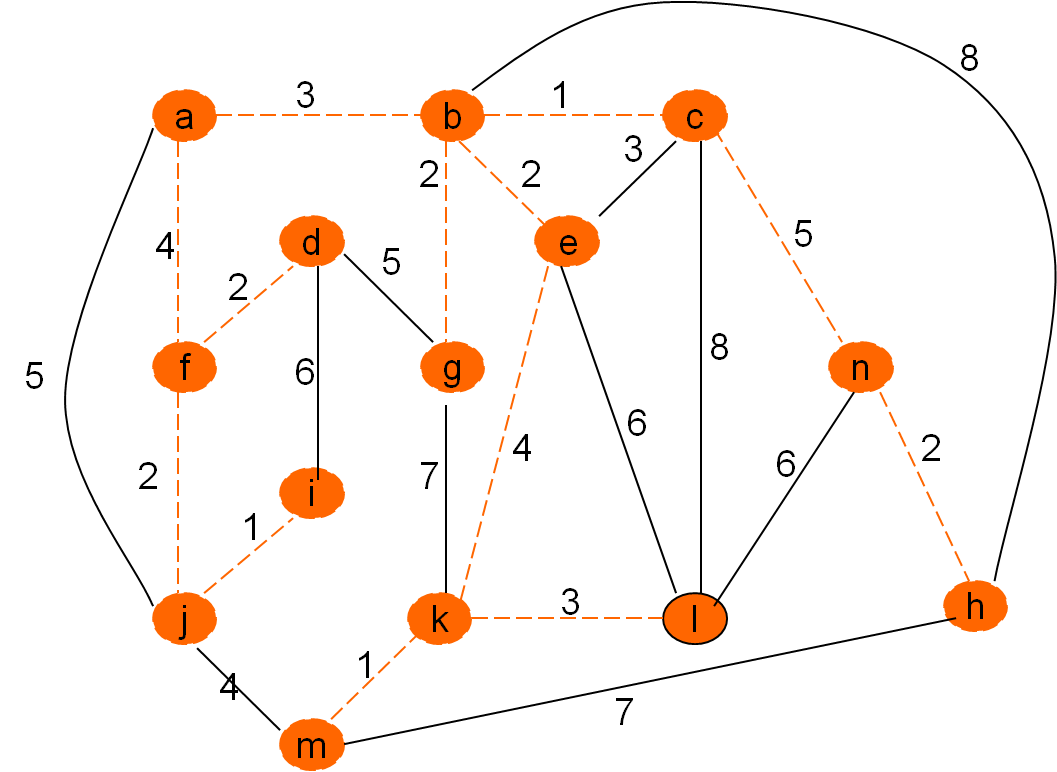
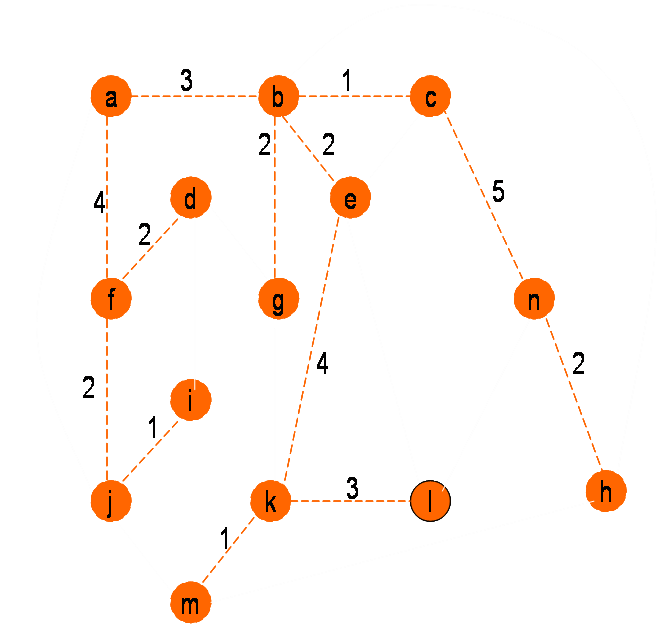
Minimalno vpeto drevo po Kruskalovem postopku
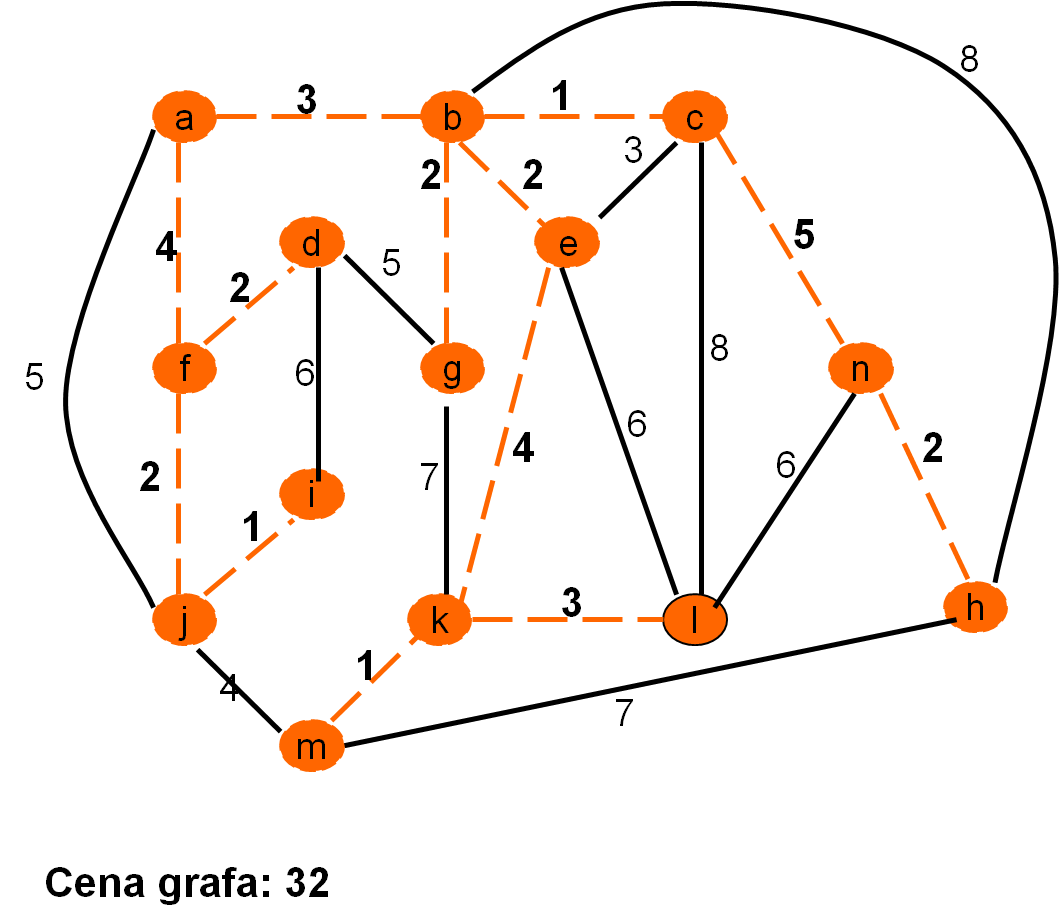
Primerjava končnih grafov
|
|
Enakost minimalnih vpetih dreves
- Enakost minimalnih vpetih dreves je slučaj, ne pravilo
- Postopka v splošnem lahko vrneta različni minimalni vpeti drevesi