| Poznamo lepa, srečna, okrogla, trikotna, kvadratna, prijateljska, popolna in še kakšna števila. Neodvisno od naših doživetij, povezanih s števili, pa v matematiki glede na naravo števil samih ločimo naravna, cela, racionalna in realna števila. Vse je odvisno od tega, kaj opazujemo. Pa bodimo radovedni... |
Kakšna števila poznamo
Figurativna števila
Vsak ima svoja lepa in srečna števila. O okroglih številih običajno govorimo pri okroglih obletnicah, na primer deseti, trideseti, stoti in podobno. Trikotniška in kvadratna števila pa sodijo v skupino figurativnih števil, ki so jih opevali že stari Grki. To so števila, ki jih v obliki pik lahko sestavimo v trikotnik, kvadrat, petkotnik in tako naprej. Za lažjo predstavo si oglej spodnjo sliko. Na njej je predstavljenih prvih nekaj trikotniških in kvadratnih števil. Z zeleno piko lahko določiš, koliko takih števil želiš videti.
Figurativna števila
Do figurativnih števil pridemo na dva načina. Lahko si preprosto narišemo ustrezne like in preštejemo pike, ali pa ugotovimo, kakšno je pravilo - kako dobimo poljubno figurativno število. Aha, pike lahko preštejemo! To pomeni, da so figurativna števila vedno lepa. Lepa v smislu, da niso negativna ali zapisana z ulomkom. Števila, s katerimi štejemo, so nam nasploh najbližja. Tako so logična, da so dobila ime kar naravna števila. Množico naravnih števil zapišemo tako:
Toda pri večjih figurativnih številih je štetje pik zamudno. Poskusi ugotoviti, katero je šesto trikotniško število in katero je šesto kvadratno. Vidiš pravilo?
Šesto trikotniško število je .
Šesto kvadratno število je .
Pravilno
Šesto trikotniško število je k petemu smo morali prišteti oziroma sešteti števila od do
Tako se prav lepo vidi tudi pravilo: -to trikotniško število je enako vsoti števil od do
Šesto kvadratno število je Tukaj je pravilo še lažje: -to kvadratno število je enako
Napačno
Še enkrat poskusi.
Rešitev
Šesto trikotniško število je k petemu smo morali prišteti oziroma sešteti števila od do
Tako se prav lepo vidi tudi pravilo: -to trikotniško število je enako vsoti števil od do
Šesto kvadratno število je Tukaj je pravilo še lažje: -to kvadratno število je enako
Prijateljska in popolna števila
Pitagoro so nekoč vprašali: "Kaj je prijatelj?" Legenda pravi, da je odgovoril: "Tisti, ki je moj drugi jaz." Potem je začudenemu sogovorniku pojasnil: "Tisti, ki je moj drugi jaz, kakor sta si 220 in 284." In v kakšni povezavi sta števili 220 in 284? Vsota deliteljev števila 220 (brez 220) je enaka 284 in vsota deliteljev števila 284 (brez 284) je enaka 220. Dve števili sta prijateljski, če je vsota deliteljev prvega števila (brez tega števila) enaka drugemu številu in obratno. Vidimo, da so včasih številom pripisovali človeške lastnosti.
Naravna števila lahko klasificiramo še na več načinov. Ena možnost je delitev na soda in liha števila. Tudi ta delitev je povezana z deljivostjo: Soda števila so deljiva z 2, liha pa ne. Z delitelji pa pridemo tudi do razvrščanja števil na nezadostna, popolna in bogata: Število je nezadostno, če je vsota njegovih deliteljev (brez tega števila) manjša od števila. Če je ta vsota enaka številu, je število popolno, če pa je večja od števila, je število bogato.
Prijateljska in popolna števila
Oglejmo si nekaj primerov:
Število 8 ima delitelje 1, 2 in 4 (8 ne štejemo zraven). Njihova vsota je 7, kar je manjše od 8. Torej je število 8 nezadostno.
Število 24 ima delitelje 1, 2, 3, 4, 6, 8 in 12 (24 ne štejemo). Njihova vsota je 36, kar je večje od 24. Torej je število 24 bogato.
Na spodnji sliki lahko premikaš krogce. Poskusi tako števila prestaviti v ustrezen koš.
Negativna števila

| 
| 
|
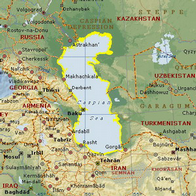
Videli smo, da so naravna števila prav čudovita. Vendar z njimi ne moremo zapisati vseh količin, s katerimi se srečamo. Kako bi zapisali temperaturo zraka na Arktiki, od koder sta pingvina s prve slike? Kako bi na zemljevidih označili depresije, to so območja, katerih višina je nižja od morske gladine? Kako bi bilo na bančnem izpisu zapisano, da smo porabili več, kot smo imeli? Če vpeljemo negativna števila, so odgovori zelo preprosti: Povprečna zimska temperatura na Arktiki je -37°C, kar pomeni 37 stopinj Celzija pod ničlo. Višina gladine Kaspijskega jezera je -28 m, to pomeni 28 m pod morsko gladino. Kaspijsko jezero je največje na svetu, njegova površina je kar 371000 Druga slika zgoraj je njegova satelitska slika, na tretji sliki pa je zemljevid. V slovenščini mu kljub velikosti in slanosti pravimo jezero, ker je stoječa celinska voda. Manjka nam še bančni izpisek: Če bi porabili 20 evrov več, kot smo jih imeli, bi bilo napisano, da je stanje na računu -20 €.
Negativna števila
Vidimo, da včasih preprosto ne gre brez negativnih števil. Omenjena negativna števila so še vedno podobna naravnim številom, le minus imajo spredaj. Če množico naravnih števil razširimo z ničlo in lepimi negativnimi števili (naravna števila z minusom), dobimo novo številsko množico. Se spomniš, kako se imenuje?
Nova številska množica se imenuje množica števil.
Pravilno
Zapiše se tako:
Napačno
Še enkrat poskusi.
Rešitev
Nova številska množica se imenuje množica celih števil.
Zapiše se tako:
Deli celote

| 
| 
|

| 
| 
|
Deli celote
Začeli smo z naravnimi števili, s katerimi lahko štejemo. Dodali smo jim ničlo in negativna cela števila (naravna števila z minusom) in tako prišli do množice celih števil. Tudi naravna in cela števila nam ne zadoščajo za vse količine. Kako bi s celimi števili opisali količine na prejšnjih slikah? Morali bi opisati, kaj imamo: Na prvi sliki je cel hlebec, to je 1 hlebec. Na drugi sliki je hlebec razdeljen na dva enaka dela, na tretji na štiri enake dele in na četrti na osem enakih delov. Na peti sliki je sedem kosov hlebca, razdeljenega na osem enakih delov, na zadnji sliki pa so trije taki kosi. Kar precej zakomplicirano in dolgo...
Na srečo obstajajo tudi števila, ki predstavljajo prav take količine. Reče se jim racionalna števila in običajno jih zapišemo z ulomkom s celim števcem in imenovalcem. Znaš količine s prejšnjih slik predstaviti z ulomki? Označi pravilni odgovor.
Pravilno
Napačno
Namig: Števec je zgoraj, šteje, koliko delov imamo. Imenovalec je spodaj, imenuje dele celote, pove, na koliko delov je razdeljena celota. Med števcem in imenovalcem je ulomkova črta.
Deli celote
Deli celote so prva racionalna števila, s katerimi smo se srečali. To je bilo že v tretjem razredu osnovne šole. Kasneje smo izvedeli, da je racionalno število širši pojem. Racionalno število predstavlja razmerje med dvema poljubnima količinama, če to razmerje lahko zapišemo z ulomkom s celim števcem in imenovalcem. Torej ni nujno, da je to razmerje med delom in celoto. Lahko opazujemo na primer razmerje med dolžino in širino omare, sobe, hiše... Množico racionalnih števil lahko zapišemo tako:
Imenovalec ne sme biti enak 0, saj tak ulomek nima pomena. O tem bomo še govorili.
Manjkajoči koščki
Pitagorejci so že v 5. stoletju pr. n. št. vedeli, da se vseh količin ne da predstaviti s celoštevilskim razmerjem, to je z racionalnimi števili. Prva taka količina, ki so jo našli, je bila diagonala kvadrata s stranico dolgo 1 enoto. Oglejmo si razmerje med stranico in diagonalo v kvadratu. Na spodnji sliki lahko premikaš krogec in tako spreminjaš velikost kvadrata. Sproti se izpisuje, kolikšno je iskano razmerje. Kaj opaziš?
Manjkajoči koščki
Opazimo, da je razmerje vedno enako:
In je eden od manjkajočih koščkov, tega števila namreč ne moremo zapisati z ulomkom s celim števcem in imenovalcem. Taka števila imenujemo iracionalna števila. Če združimo racionalna in iracionalna števila, dobimo novo številsko množico - množico realnih števil. Z realnimi števili lahko predstavimo vse količine, ki nas obkrožajo v realnem svetu.
Bistveno vprašanje, ki se zdaj pojavi, je, kako ločimo racionalno in iracionalno število? Vemo, da racionalno število lahko zapišemo z ulomkom s celim števcem in imenovalcem, iracionalnega števila pa ne. Toda kako naj se prepričamo, da nekega števila ne moremo zapisati z ulomkom s celim števcem in imenovalcem? Čisto matematični način bi bil dokaz, do katerega pridemo kasneje. Obstaja pa tudi bližnjica, ki se imenuje decimalni zapis. Upam, da se vsi spomnimo, da je decimalni zapis sestavljen iz celega dela, decimalne vejice in decimalk. Ulomek spremenimo v decimalni zapis tako, da zdelimo števec in imenovalec. Lahko si pomagamo s kalkulatorjem. Decimalni zapis nam takoj pove, katero število je racionalno in katero iracionalno: Decimalni zapis racionalnih števil je bodisi končen bodisi periodičen (nekaj decimalk se stalno ponavlja), decimalni zapis iracionalnih števil pa je vedno neskončen in neperiodičen, decimalke se zdijo povsem naključne.
Manjkajoči koščki
Hitro vzemi kalkulator in ugotovi, kateri ulomki predstavljajo racionalna števila in kateri iracionalna. Poveži!
Pravilno
Napačno
Še enkrat poskusi.
Rešitev
| Iracionalno | |
| Racionalno | |
| Iracionalno | |
| Racionalno | |
| Racionalno | |
| Racionalno |
Manjkajoči koščki
Razvrščanje števil v številske množice ni tako enostavno, kot je videti na prvi pogled. Ampak počasi nam bo šlo, številske množice bomo kmalu podrobneje spoznali.
Dodatne naloge 1
Izračunaj deseto trikotniško število in ugotovi, ali je tudi trikotniško število.
Deseto trikotniško število je .
Pravilno
Napačno
Še enkrat poskusi.
Rešitev
Deseto trikotniško število je ni trikotniško število, dvanajsto trikotniško število je
Dodatne naloge 2
Izračunaj dvanajsto kvadratno število in ugotovi, ali je tudi kvadratno število.
Dvanajsto kvadratno število je .
Pravilno
Napačno
Še enkrat poskusi.
Rešitev
Dvanajsto kvadratno število je je trinajsto kvadratno število.
Dodatne naloge 3
Pravilno
Napačno
Še enkrat poskusi.
Rešitev
Nepopolna so števila in Bogato je število Popolno ni nobeno.
Dodatne naloge 4
Pravilno
Napačno
Še enkrat poskusi.
Rešitev
Cela so števila so in
Dodatne naloge 5
Pravilno
Napačno
Še enkrat poskusi.
Rešitev
| Naravno število | |
| Racionalno število | |
| Realno število | |
| Celo število | |
| Realno število | |
| Naravno število | |
| Realno število |
Dodatne naloge 6
Ugotovi, kateri od danih ulomkov predstavljajo racionalno število in kateri iracionalno ter poveži.
Pravilno
Napačno
Še enkrat poskusi.
Rešitev
| Iracionalno | |
| Racionalno | |
| Iracionalno | |
| Iracionalno | |
| Iracionalno |