| Kako konstruiramo ? To število je iracionalno, kar pomeni, da ga ne moremo zapisati z ulomkom. |
Koren iz 2
Koren iz 2
E-um (vsebinsko), Skupina NAUK (tehnično)
Diagonala v kvadratu
Koliko meri diagonala v kvadratu s stranico ?
Pravilno
Pokukaj za skico. Skica
Napačno
Še enkrat poskusi. Pokukaj za skico. Skica
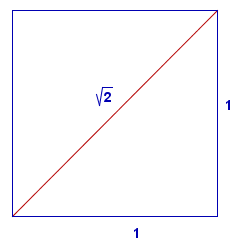
Konstrukcija
Na spodnjem apletu je prikazana konstrukcija .
Konstrukcijo postaviš na začetek s klikom na desni gumb. Naslednji konstrukcijski korak se pokaže, ko klikneš na srednji gumb.
Poskusi si sam razložiti konstrukcijo.
Konstrukcija
Koraki konstrukcije:
- Narišeš pravokotnico na številsko premico skozi točko
- Na tej premici odmeriš dolžino
- Dobljeno točko povežeš z izhodiščem. Daljica, ki jo dobiš, meri
- S šestilom dobljeno daljico odmeriš na številski premici.
Dokaz s protislovjem
Števila ne moremo zapisati z ulomkom. Preden to utemeljimo, si oglejmo poseben način dokazovanja.
Bistvo takega načina dokazovanja je, da na začetku privzamemo neko predpostavko. Z logičnim sklepanjem iz te predpostavke in drugih trditev pridemo do nesmisla oziroma protislovja s privzeto predpostavko na začetku. Torej smo narobe predpostavili.
Če na začetku rečemo, da je neka izjava pravilna, in nato pridemo do protislovja, potem mora veljati, da je prvotna izjava nepravilna.
Iskanje morilca
V parku se je zgodil umor. Policija zasliši 3 osumljence. Jack pravi, da je bil na zabavi s Tomom na drugem koncu mesta. John trdi, da je bil na zabavi skupaj z Jackom in Tomom. Tom prizna umor. Natanko eden izmed njih laže.
Detektiv Holmes je razmišljal takole: "Ali je lahko Tom res morilec?"
Holmes je razmišljal naprej.
Recimo, da je Tom res morilec. Torej govori resnico. Potem nista morilca Jack ali John in eden izmed njiju laže. Če Jack govori resnico, je bil Tom z Jackom. Če pa govori resnico John, je bil Tom z obema. Kar pomeni, da Tom ni bil v parku.
Holmes se zamisli: "Torej je nekaj narobe. Le kje sem se zmotil? Aha, moja predpostavka, da je Tom morilec, je bila napačna." Torej Tom ni morilec.
Recimo, da je Tom res morilec. Torej govori resnico. Potem nista morilca Jack ali John in eden izmed njiju laže. Če Jack govori resnico, je bil Tom z Jackom. Če pa govori resnico John, je bil Tom z obema. Kar pomeni, da Tom ni bil v parku.
Holmes se zamisli: "Torej je nekaj narobe. Le kje sem se zmotil? Aha, moja predpostavka, da je Tom morilec, je bila napačna." Torej Tom ni morilec.
Pravilno
Napačno
Koren 2 ni racionalno število
Dokaz bomo naredili s protislovjem, kar pomeni: "Recimo, da je racionalno število."
Spomni se: vsako racionalno število lahko zapišemo z okrajšanim ulomkom:
kjer sta in tuji števili, torej je ulomek okrajšan.
Iščemo ulomek, katerega kvadrat je enak zato mora veljati
Odpravimo ulomke, sledi
Velja: torej je število deljivo z kar pomeni, da je sodo. Spomni se, da je produkt dveh sodih števil sodo število, dveh lihih števil pa liho število. Kar pomeni, da je sodo število.
Verjetno se spomniš, da so vsa soda števila večkratniki števila Spomni se: število je sodo, zato ga lahko zapišeš kot
Enakost za vstavi v enakost
Iz vseh zvez od zgoraj dobiš:
Skoraj si že na koncu. Izrazi
Koren 2 ni racionalno število
Želiš dobiti podobno zvezo kot med in Velja:
Kaj lahko poveš o številih in glede sodosti oziroma lihosti?
Velja: zato je število sodo, prav tako pa tudi število
Ugotovil si, da sta števili in sodi, torej sta deljivi z
Če imata števili skupnega delitelja pomeni, da nista tuji. Torej ulomek ni okrajšan. To pa je v nasprotju s tistim, kar si privzel na začetku.
Ker nikjer vmes nisi napačno sklepal, je bila napačna predpostavka, da je število možno zapisati z okrajšanim ulomkom.
Konstrukcija korena iz 3
Spodaj je prikazana konstrukcija števila , kjer si spet pomagamo s Pitagorovim izrekom. Iskano število konstruiramo tokrat na kateti pravokotnega trikokotnika.
Na začetek konstrukcije se postaviš z levi gumbom.
Konstrukcija korena iz 3
Število lahko konstruiramo s pomočjo števila , kakor je prikazano na spodnji sliki.
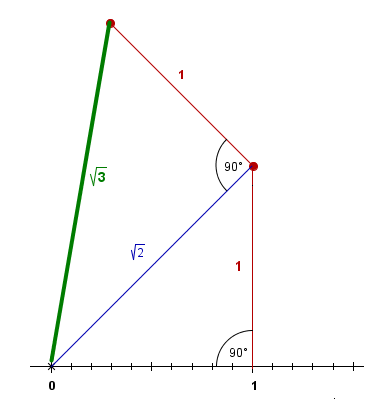
Konstrukcija korena iz 3
Utemeljitev prejšnje konstrukcije. Zakaj zelena daljica meri ?
Na začetku smo pokazali, da modra daljica res meri . Na to daljico narišemo novo pravokotnico in na njej odmerimo daljico dolžine Spet imamo pravokotni trikotnik. Torej zelena daljica res meri , kar sledi iz Pitagorovega izreka.
Nadaljuj konstrukcijo, prikazano na prejšnji strani, in tako konstruiraj vsaj še kvadratne korene števil. To bodo naslednja števila: in
Konstrukcija kvadratnih korenov
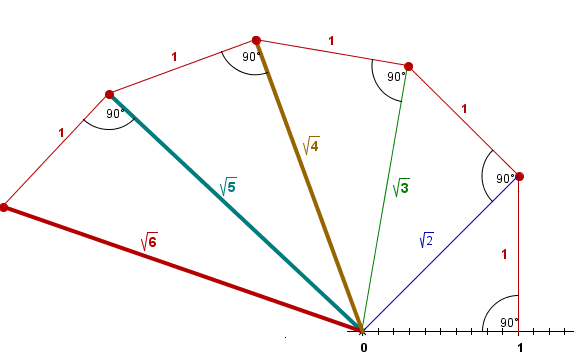
Dodatne naloge 1
Pravilno
|
|
Napačno
Še enkrat poskusi.
Rešitev
|
|
Dodatne naloge 2
S pomočjo pravokotnega trikotnika konstruiraj število samo z enim trikotnikom. Označi pravilno rešitev.
Pravilno
Napačno
Še enkrat poskusi.
Rešitev
Dodatne naloge 3
S pomočjo pravokotnega trikotnika konstruiraj število samo z enim trikotnikom. Označi pravilno rešitev.
Pravilno
Napačno
Še enkrat poskusi.
Rešitev
Dodatne naloge 4
Dokaži, da ni racionalno število. Pomagaj si z rešitvijo.
Predpostavi, da lahko zapišeš z okrajšanim ulomkom Torej števili in nimata skupnega delitelja. S kvadriranjem enakosti dobiš: Podobno kot pri enakost obrneš. Iz enakosti sledi, da deli tako kot tudi Število je torej večkratnik števila : To vstaviš v enakost in s krajšanjem dobiš: Podobno kot v prejšnjem primeru sta števili in deljivi s Torej števili in nista
tuji, saj sta obe števili večkratnika števila Kar pomeni, da predpostavka, da lahko zapišemo z okrajšanim ulomkom, ne drži.
