Definicijsko območje polinoma je cela realna os, zato lahko vrednost polinoma izračunamo za poljubno realno število .
Če poskušamo vrednost polinoma višje stopnje v neki točki izračunati brez pomoči kalkulatorja, pa ugotovimo, da potrebujemo za izračun vrednosti zelo veliko operacij in da večino časa delamo z zelo velikimi števili.
Hornerjev algoritem 1
Vrednost polinoma v točki
1. primer
Odlično! Nalogo si rešil pravilno.
REŠITEV
Odgovor ni pravilen. Poskusi še enkrat.
1. primer
Če bi isto nalogo zadali srednješolcu v višjem letniku, bi jo rešil takole:
Ni nam sicer še čisto jasno, kako je prišel do enakega rezultata, vidimo pa lahko, da je uporabil manj množenj, v katerih so se pojavljala relativno majhna števila.
1. primer
Čarovnija se skriva v Hornerjevem algoritmu, postopku, ki bistveno zmanjša število potrebnih množenj in na zelo ekonomičen način izračuna vrednost polinoma v točki.
Poglejmo si še enkrat izraz in ga preoblikujmo:

Na videz smo dobili še bolj kompliciran izraz kot prej. V resnici pa smo zelo zmanjšali število množenj in prevedli nalogo na računanje z manjšimi števili (npr. samo za računanje potence so potrebna štiri množenja, tukaj pa smo vsega skupaj množili štirikrat).
1. primer
Izračunajmo vrednost danega izraza.
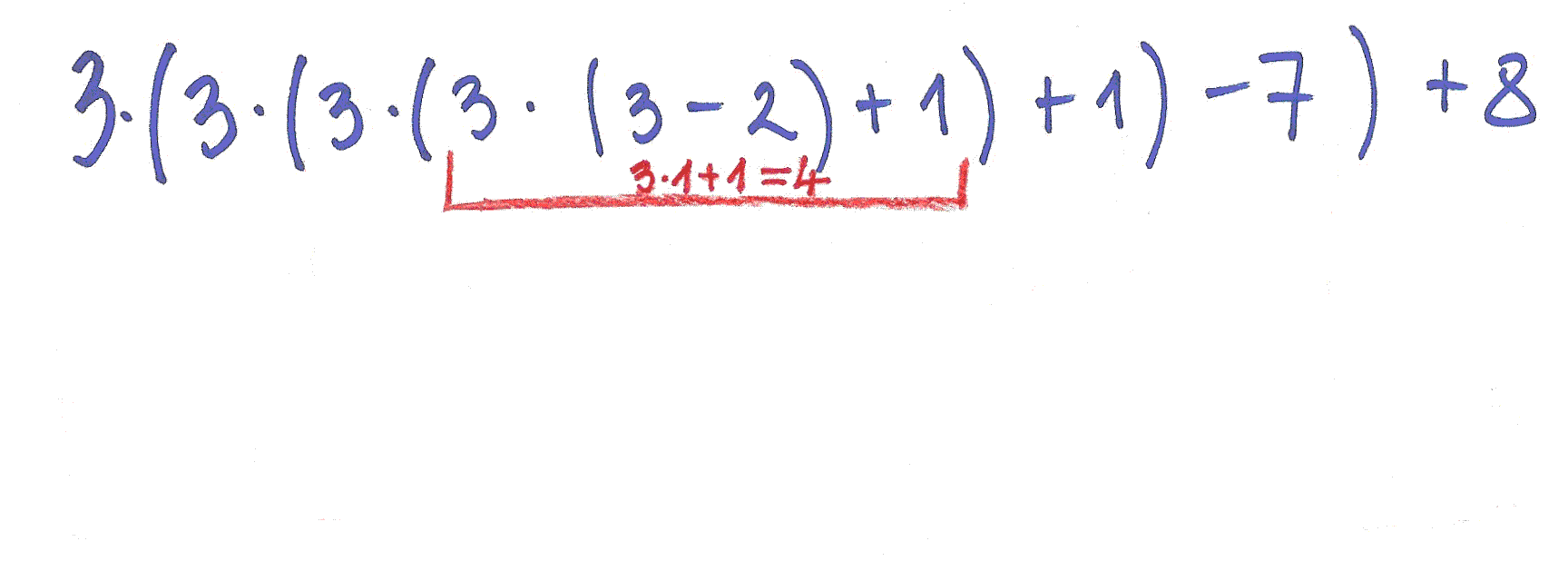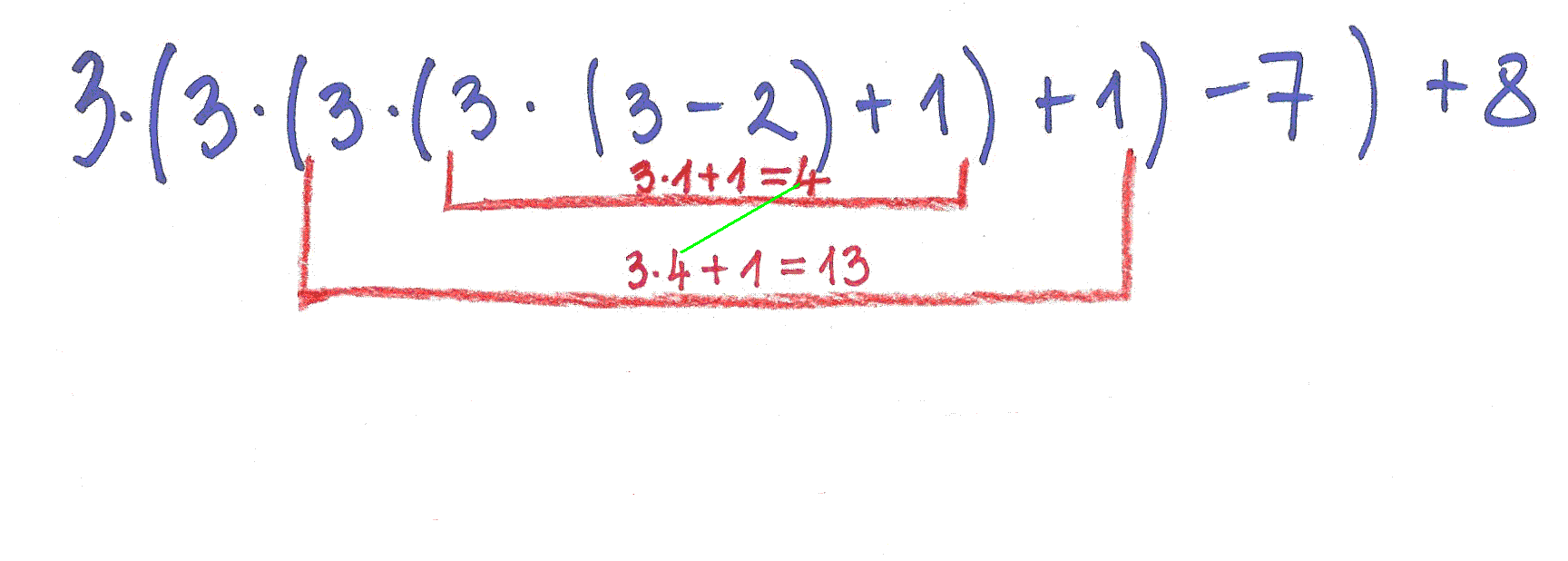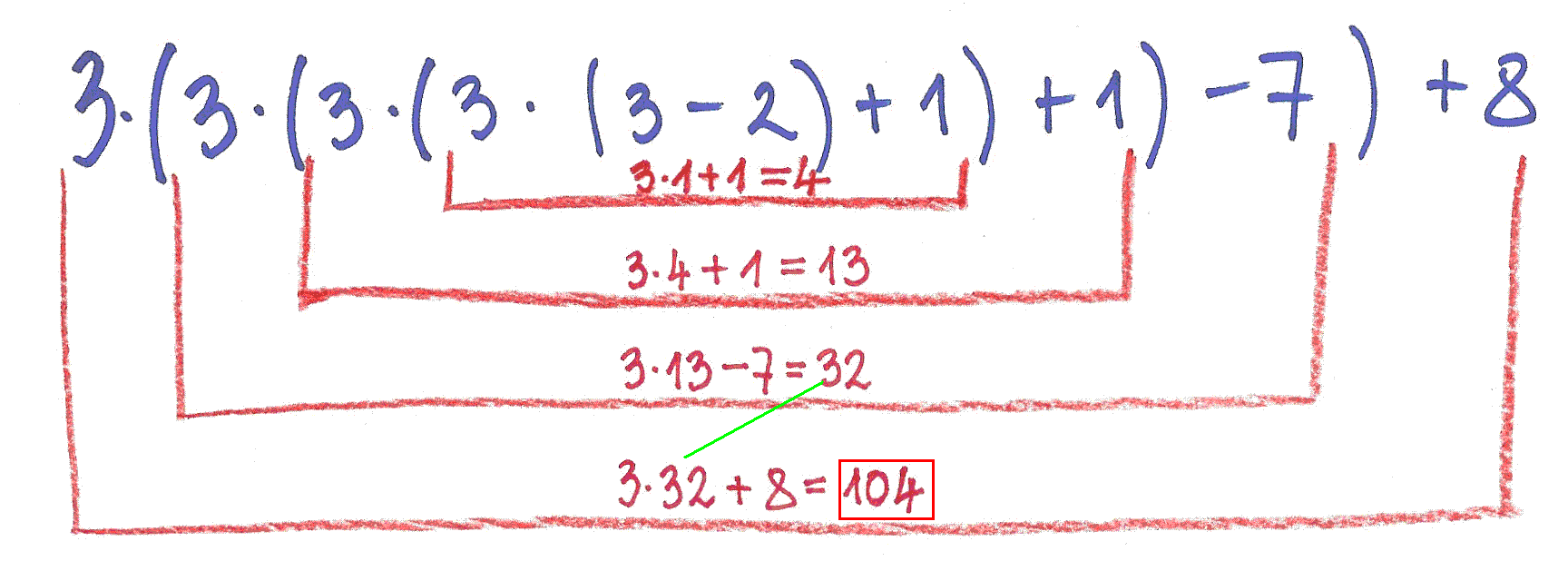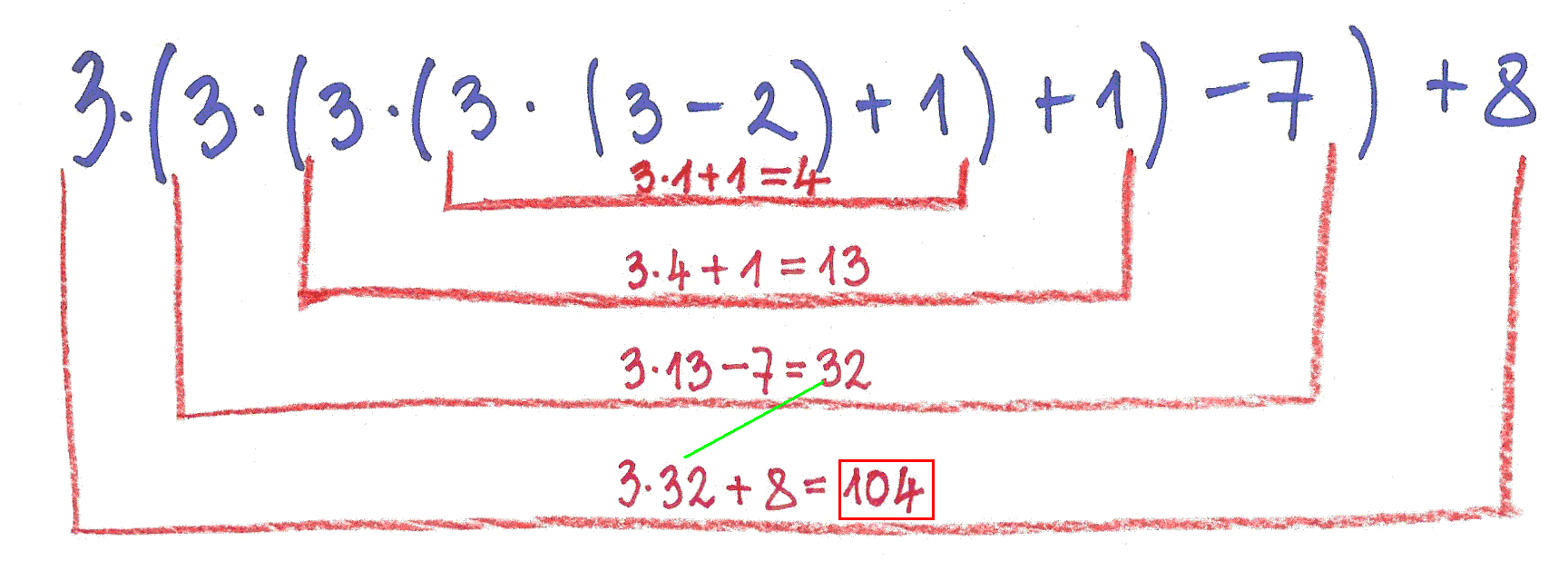
1. primer
Sedaj pa pozorno opazuj spodnji shemi, po katerih smo izračunali vrednost polinoma za in odgovori na naslednja vprašanja.
| 1. | Kje v polinomu se pojavijo števila v prvi vrstici desne sheme? | Odgovor | |
| 2. | Kako dobimo števila v drugi vrstici desne sheme? | Odgovor | |
| 3. | Kako dobimo števila v tretji vrstici desne sheme? | Odgovor |
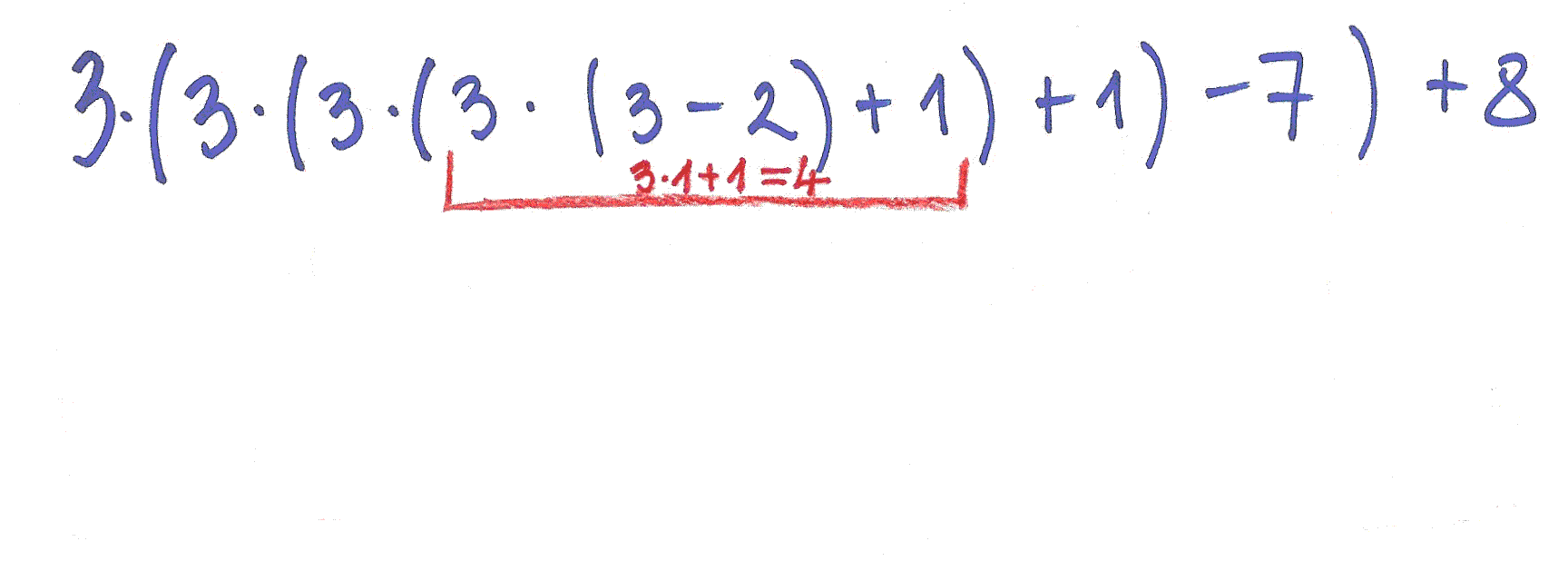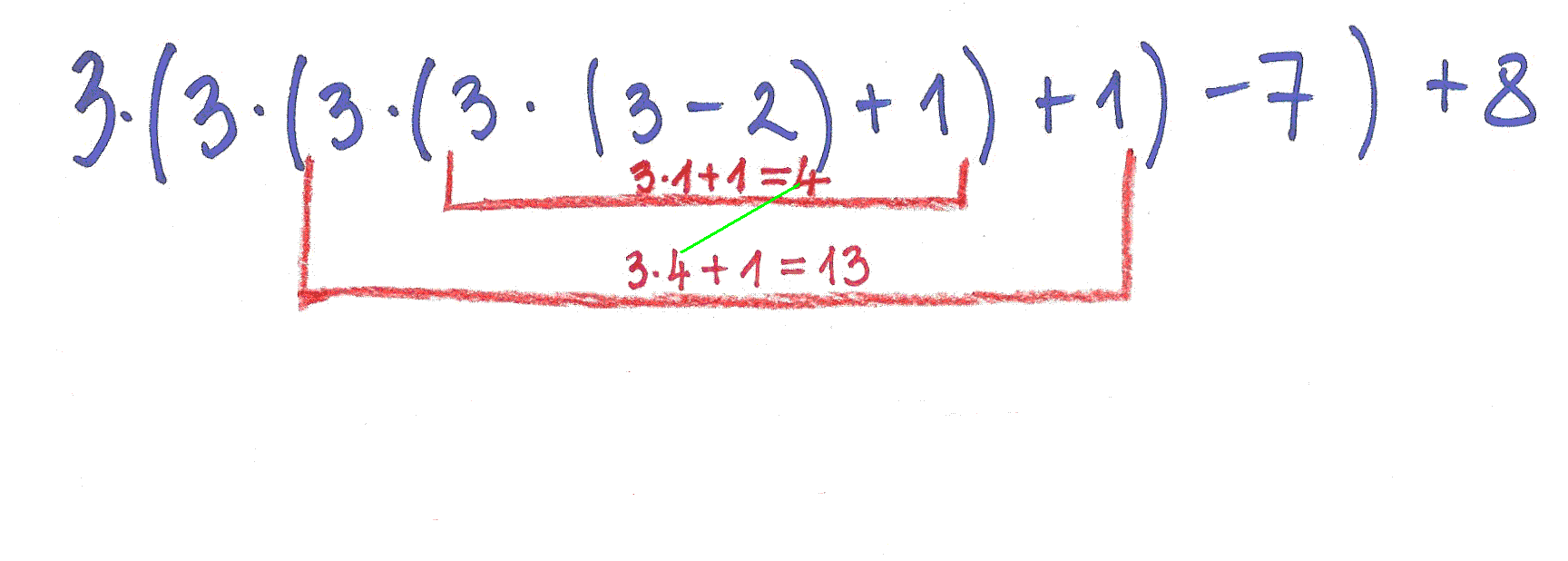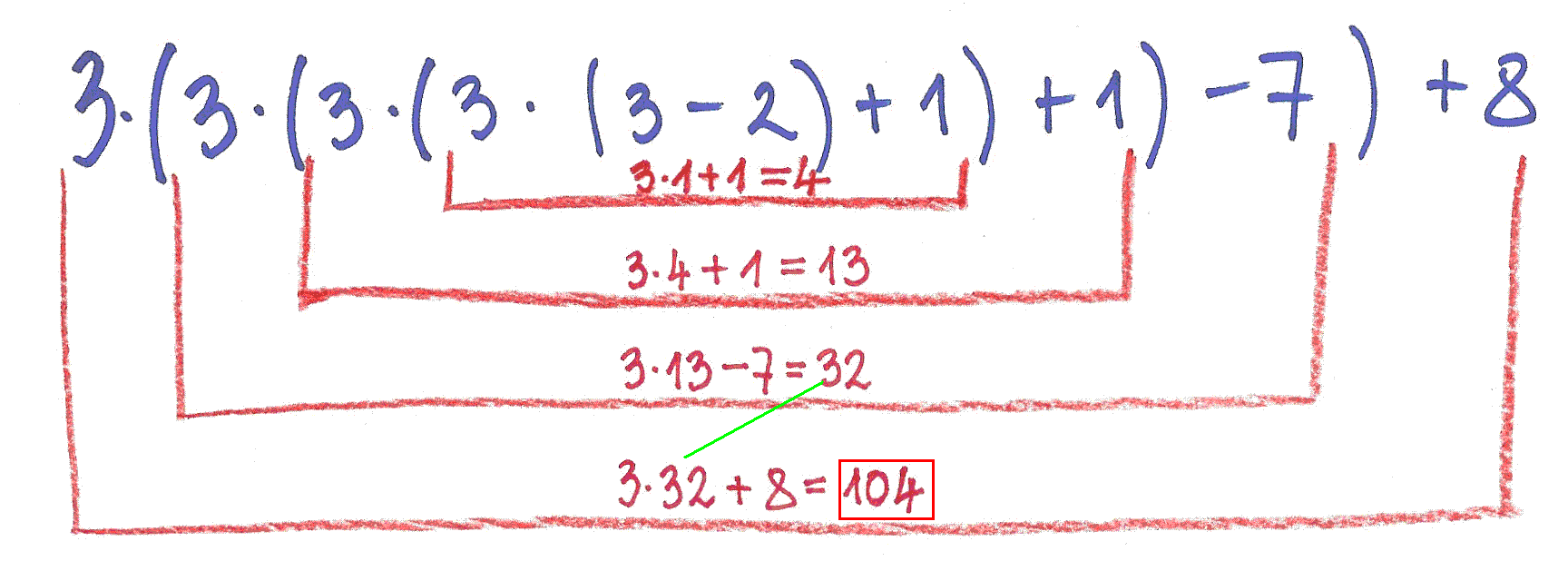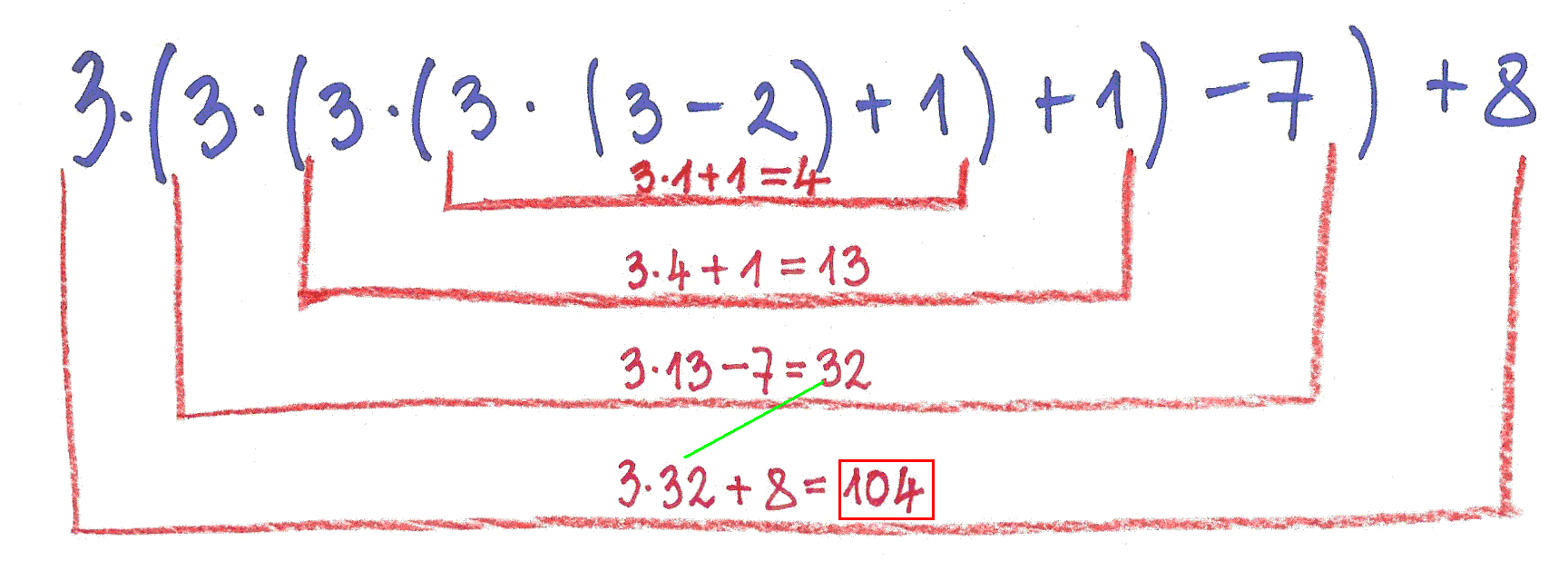
|
Ta postopek se imenuje Hornerjev algoritem.
Števila v prvi vrstici sheme so koeficienti polinoma.
V spodnji levi kot zapišemo število, za katerega želimo izračunati vrednost polinoma (v našem primeru ). Do števil v drugi vrstici pridemo z množenjem števil v tretji vrstici z izbranim številom.
Do števil v tretji vrstici pridemo tako, da seštejemo število v prvi in drugi vrstici.
2. primer
Izračunajmo vrednost polinoma v točki s pomočjo Hornerjevega algoritma.
Na spodnji sliki imaš predstavljen Hornerjev algoritem po korakih.
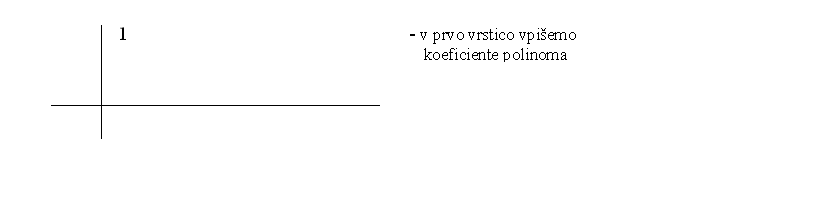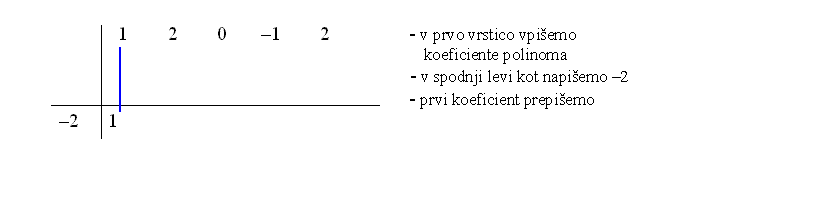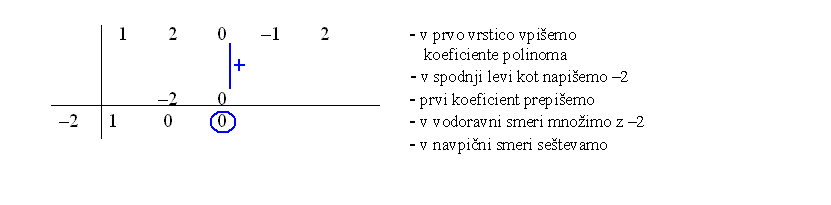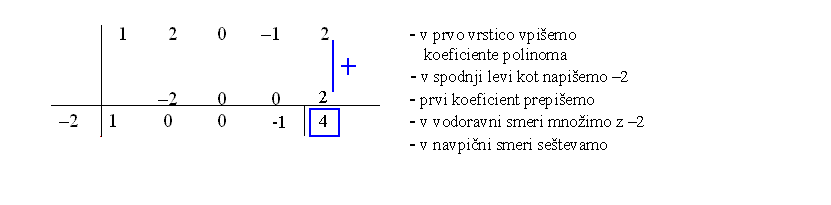
Vrednost polinoma v točki preberemo v zadnji vrstici. Torej .
3. primer
Izračunaj vrednost polinoma za . V pripravljeno tabelo za Hornerjev algoritem vpisuj ustrezna števila.
Odlično! Nalogo si rešil pravilno.
Torej . Sedaj znaš tudi ti izračunati vrednost polinoma v neki točki s pomočjo Hornerjevega algoritma.
REŠITEV
Napačno
Odgovor ni pravilen. Poskusi še enkrat.
Hornerjev algoritem v splošnem
Za radovedne predstavimo še Hornerjev algoritem v splošnem.
Naše ideje in razmišljanje na konkretnem primeru lahko formalno zapišemo takole:
| = | |
| = | |
| = | |
| = | |
| = |
Hornerjev algoritem v splošnem
Tako lahko vrednost polinoma določimo v več zaporednih korakih. Začnemo pri najbolj notranjem oklepaju in nadaljujemo proti zunanjim:
Zato je
Hornerjev algoritem v splošnem
Rekurzivni postopek nam privarčuje vsakratno računanje potenc , je pa sprva videti nepregeden in zapleten. Zato si običajno računanje lažje predstavimo z naslednjo (že na pol znano) tabelico.
Pripravimo si tri vrstice. V zgornjo vrstico napišemo koeficiente polinoma v (glede na pripadajoče potence) padajočem vrstnem redu, zamaknjene za ena v desno, drugo vrstico pustimo zaenkrat prazno, v tretjo pa v skrajni levi kot napišemo :
| ... | ||||||
| x |
Hornerjev algoritem v splošnem
Potem v predpisanem vrstnem redu izpolnjujemo prazna mesta v tabelici. Najprej v tretjo vrsto, zraven , iz prve vrste prepišemo .
| ... | ||||||
| x |
Potem si predstavljamo, da množimo in produkt napišemo v celico, ki leži za ena višje in ena bolj v desno. Vrednosti v drugem stolpcu seštejemo.
| ... | ||||||
| x |
Sedaj s pomočjo prejšnjih enakosti ugotovimo, da velja
Hornerjev algoritem v splošnem
Postopek nadaljujemo na enak način. Ponovno pomnožimo z in produkt napišemo v celico, ki leži za mesto višje in za mesto v desno. Vrednosti v stolpcu seštejemo in vsoto napišemo v trejo vrstico.
| ... | |||||||
| x |
S postopkom nadaljujemo do konca tabelice. Na koncu dobimo Hornerjev algoritem za izračun vrednosti polinoma v točki .
| ... | |||||||
| x |
V tabelici je v desnem spodnjem kotu vrednost .
W. G. Horner

| 
|
| William George Horner, (1786-1837) | Horner je izumil napravo, ki so jo v viktorijanskih časih imenovali zoetrope in je predhodnica kina. S hitrim vrtenjem statičnih fotografij je dosegel na videz zvezno premikanje. |
Naloge
1. naloga
S pomočjo Hornerjevega algoritma izračunaj vrednost polinoma v izbrani točki .
Odgovor: Vrednost polinoma v izbrani točki je
Odlično! Nalogo si rešil pravilno.
REŠITEV
Odgovor: Vrednost polinoma v izbrani točki je .
Odgovor ni pravilen. Poskusi še enkrat.
Naloge
2. naloga
S pomočjo Hornerjevega algoritma izračunaj vrednost polinoma v izbrani točki .
Odgovor: Vrednost polinoma v izbrani točki je
Odlično! Nalogo si rešil pravilno.
REŠITEV
Odgovor: Vrednost polinoma v izbrani točki je .
Odgovor ni pravilen. Poskusi še enkrat.
Naloge
3. naloga
S pomočjo Hornerjevega algoritma izračunaj vrednost polinoma v izbrani točki .
Odgovor: Vrednost polinoma v izbrani točki je
Odlično! Nalogo si rešil pravilno.
REŠITEV
Odgovor: Vrednost polinoma v izbrani točki je .
Odgovor ni pravilen. Poskusi še enkrat.
Naloge
4. naloga
S pomočjo Hornerjevega algoritma izračunaj vrednost polinoma v izbrani točki .
Odgovor: Vrednost polinoma v izbrani točki je
Odlično! Nalogo si rešil pravilno.
REŠITEV
Odgovor: Vrednost polinoma v izbrani točki je .
Odgovor ni pravilen. Poskusi še enkrat.
Naloge
5. naloga
S pomočjo Hornerjevega algoritma izračunaj vrednost polinoma v izbrani točki .
Odgovor: Vrednost polinoma v izbrani točki je
Odlično! Nalogo si rešil pravilno.
REŠITEV
Odgovor: Vrednost polinoma v izbrani točki je .