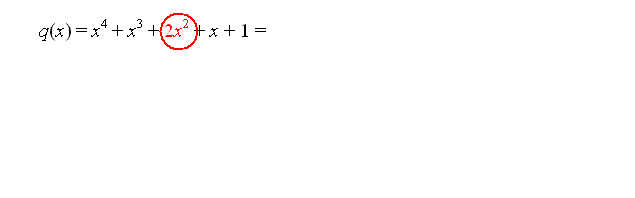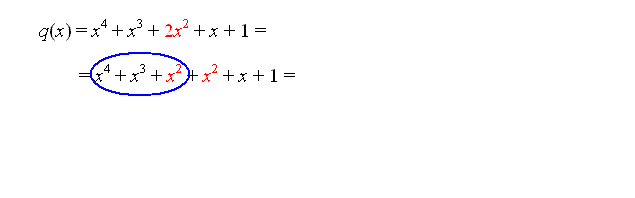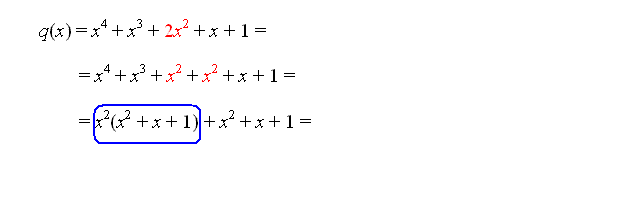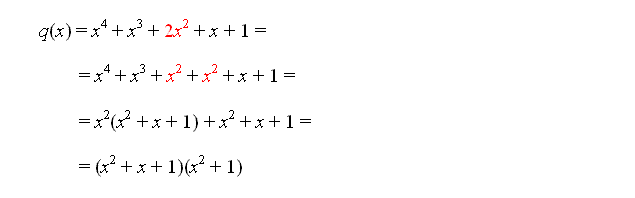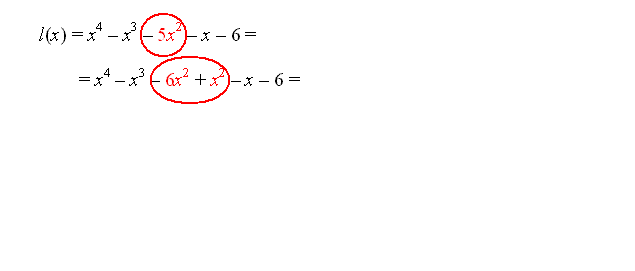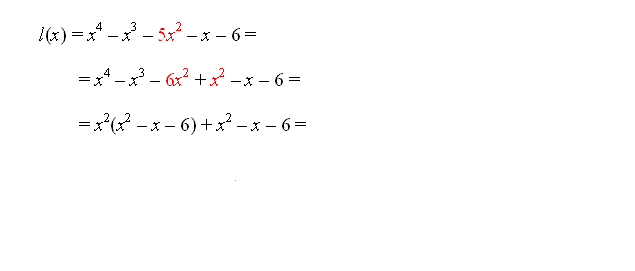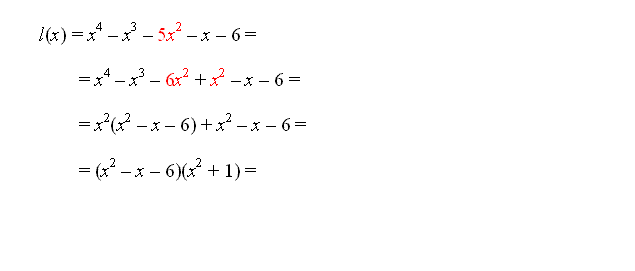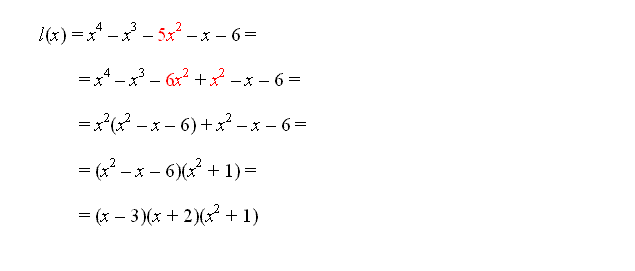Z razcepljanjem izrazov smo se že velikokrat srečali, predvsem smo razcepljali razliko kvadratov, vsoto in razliko kubov, nekaj malega smo razcepljali tudi vsoto in razliko višjih potenc ter kvadratne polinome. Za vse razcepe smo poznali obrazce, ki so nam delo zelo poenostavili. Na tem mestu pa se bomo lotili tudi razcepljanja polinomov višjih stopenj, saj bomo razcepe polinomov potrebovali pri iskanju ničel polinomov.
Vendar pa razcep ne bo vedno taklo preprost kot smo bili navajeni in bo potrebno malo več spretnosti. Že za polinome stopnje pet se na primer izkaže, da v splošnem ne obstaja nobena formula, ki bi povezovala ničle polinoma z njegovimi koeficienti (za razliko od kvadratnih polinomov na primer). Celo približne numerične metode za iskanje ničel polinomov so zelo nestabilne in pogosto ne dajo dobrih rezultatov.
Za začetek si poglejmo, kdaj pravimo, da je polinom razcepen.
| Polinom je razcepen, kadar ga lahko zapišemo kot produkt vsaj dveh vsaj linearnih polinomov. |