Veverica ima v duplini 5 želodov še iz pretekle zime. V pripravi nove zaloge vsak dan v duplino prinese tri nove želode.
Koliko želodov bo imela veverica čez tri in koliko čez deset dni? Pomagaj si s spodnjo sliko.
Čez tri dni bo imela
Veverica in želodi
Veverica ima v duplini 5 želodov še iz pretekle zime. V pripravi nove zaloge vsak dan v duplino prinese tri nove želode.
Koliko želodov bo imela veverica čez tri in koliko čez deset dni? Pomagaj si s spodnjo sliko.
Čez tri dni bo imela
Še enkrat poskusi.
Čez tri dni bo imela želodov.
Veverica in želodi
Seveda je slika pregleden prikaz, vendar bi se izkazala za precej nepraktično in zamudno, če bi recimo želeli izvedeti, koliko želodov bo imela veverica čez dni. Kako bi torej izračunali stanje po desetih dneh? In po dneh?
Čez deset dni bo imela želodov.
Čez 56 dni bo imela želodov.
Še enkrat poskusi.
Veverica bo imela po desetih dneh poleg začetne zaloge ( želodov) še krat po želode, torej skupaj želodov.
Čez dni bo imela želodov.
Preizkusi se
Odgovor je napačen.
Zgoraj so navedeni trije primeri aritmetičnih zaporedij. V prvem in zadnjem primeru je vsak naslednji člen za oz. večji od prejšnjega, v drugem pa je vsak člen za manjši od prejšnjega.
Vsem trem zaporedjem je skupno to, da vsak naslednji člen dobimo tako, da prejšnjemu prištejemo isto število (lahko tudi negativno).
Definicija
Zaporedje je aritmetično, če je razlika dveh zaporednih členov konstantna. To razliko imenujemo diferenca in jo označujemo z .
Za vsak torej velja
oz. .
Vsak naslednji člen aritmetičnega zaporedja dobimo tako, da prejšnjemu prištejemo diferenco.
Poskusi sam
Štiri števila iz prvega stolpca premakni(prepiši) v tretji stolpec tako, da bo nastalo petčleno padajoče aritmetično zaporedje. Prvi člen zaporedja je že v desnem stolpcu. Če boš števila pravilno razvrstil, te bo računalnik o tem obvestil, čim klikneš na gumb "Preveri".
| -84 | = | -112 |
| -125 | = | |
| -164 | = | |
| -104 | = | |
| -151 | = | |
| -138 |
|
|
Splošni člen aritmetičnega zaporedja
Ugotovili smo že, da lahko vsak člen aritmetičnega zaporedja dobimo tako, da njegovemu predhodniku prištejemo diferenco. Razmislimo ali za izračun poljubnega člena aritmetičnega zaporedja zadostujeta le prvi člen zaporedja in znana diferenca.

Če si pozorno sledil animaciji, si verjetno prišel do naslednjega sklepa:
Diferenca je razlika dveh zaporednih členov zaporedja.
Naloga
. člen tega zaporedja je enak .
Namig:
Zaporedje je aritmetično s prvim členom in diferenco . Zanima nas . člen, torej .
Naloga
Sedaj poskusi sam oblikovati podobne naloge. S pomočjo izbranega prvega člena zaporedja in izbrane diference izračunaj poljubni člen zaporedja. Rezultat preveri s programom spodaj.
| Prvi člen = | |
| Diferenca = | |
| n = | |
Lastnosti aritmetičnega zaporedja
Sedaj, ko že znaš izračunati splošni člen aritmetičnega zaporedja, si poglejmo nekatere lastnosti tega zaporedja.
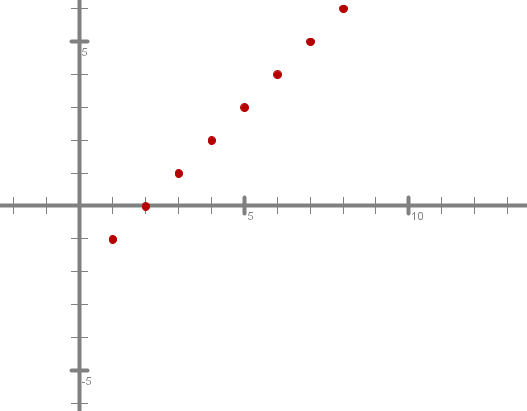
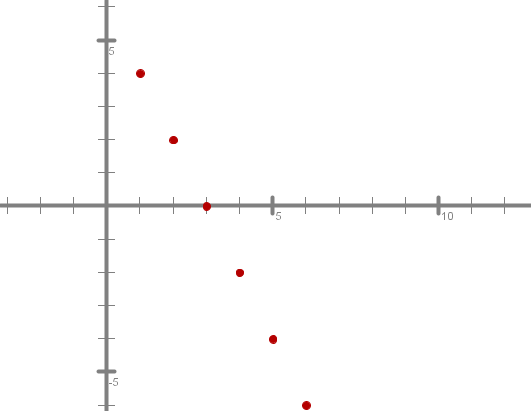
Za začetek poišči začetni člen in diferenco aritmetičnih zaporedij, katerih splošna člena sta in ter nariši grafa zaporedij. Razmisli o lastnostih.
Pomagaš si lahko s spodnjo aplikacijo, ki izračuna splošni člen in nariše graf zaporedja.
Grafi zaporedij spominjajo na grafe funkcij. Zakaj
Če bi točke grafa zaporedja med seboj povezali v premico, bi dobili graf linearne funkcije , v drugem primeru (ko bi povezali točke grafa zaporedja ) pa bi dobili graf linearne funkcije .
Monotonost in omejenost
Kako je z monotonostjo aritmetičnih zaporedij?
Kakor vidiš, je prvo zaporedje strogo naraščajoče, drugo pa strogo padajoče. Kaj vpliva na to lastnost?
Ali je tudi sicer od diference odvisno, ali bo aritmetično zaporedje naraščajoče ali padajoče?
Če želimo preveriti, ali je zaporedje naraščajoče ali padajoče, izračunamo razliko .
Če je ta pozitivna, je zaporedje strogo naraščajoče, če je negativna, pa strogo padajoče.
V aritmetičnem zaporedju je ta razlika vedno enaka diferenci: .
Če je torej diferenca pozitvna, je zaporedje naraščajoče, če je negativna, pa padajoče.
Še enkrat poskusi.
Monotonost in omejenost
Razmisli še o omejenosti aritmetičnega zaporedja.
Premisli, kdaj je aritmetično zaporedje navzgor omejeno.
In kdaj je aritmetično zaporedje navzdol omejeno?
Sedaj pa razmisli, ali je lahko aritmetično zaporedje omejeno.
Zaporedje je navzgor omejeno, kadar obstaja tako realno število , da za poljubno naravno število velja:
Denimo, da je aritmetično zaporedje naraščajoče. Za vsak naslednji člen prejšnjemu prištejemo pozitivno diferenco in slej ko prej pridemo čez vsako mejo .
Če pa je aritmetično zaporedje padajoče, potem za vsak naslednji člen prejšnjemu prištejemo negativno diferenco. Zgornja meja takega zaporedja je enaka prvemu členu: .
Aritmetično zaporedje je torej navzgor omejeno, ko je padajoče ali konstantno. V tem primeru je zgornja meja .
Zaporedje je navzdol omejeno, kadar obstaja tako realno število , da za poljubno naravno število velja: .
Denimo, da je aritmetično zaporedje padajoče. Za vsak naslednji člen prejšnjemu prištejemo negativno diferenco in slej ko prej pridemo pod vsako mejo .
Če pa je aritmetično zaporedje naraščajoče, potem za vsak naslednji člen prejšnjemu prištejemo pozitivno diferenco. Spodnja meja takega zaporedja je enaka prvemu členu: .
Aritmetično zaporedje je torej navzdol omejeno, ko je naraščajoče ali konstantno. V tem primeru je spodnja meja .
Zaporedje je omejeno, kadar je navzgor in navzdol omejeno.
Aritmetično zaporedje je omejeno, ko je hkrati naraščajoče in hkrati padajoče. Edina aritmetična zaporedja, ki ustrezajo obema zahtevama, so konstantna zaporedja.
Še enkrat poskusi.
Zaporedje je navzgor omejeno, kadar obstaja tako realno število , da za poljubno naravno število velja:
Denimo, da je aritmetično zaporedje naraščajoče. Za vsak naslednji člen prejšnjemu prištejemo pozitivno diferenco in slej ko prej pridemo čez vsako mejo .
Če pa je aritmetično zaporedje padajoče, potem za vsak naslednji člen prejšnjemu prištejemo negativno diferenco. Zgornja meja takega zaporedja je enaka prvemu členu: .
Aritmetično zaporedje je torej navzgor omejeno, ko je padajoče ali konstantno. V tem primeru je zgornja meja .
Zaporedje je navzdol omejeno, kadar obstaja tako realno število , da za poljubno naravno število velja: .
Denimo, da je aritmetično zaporedje padajoče. Za vsak naslednji člen prejšnjemu prištejemo negativno diferenco in slej ko prej pridemo pod vsako mejo .
Če pa je aritmetično zaporedje naraščajoče, potem za vsak naslednji člen prejšnjemu prištejemo pozitivno diferenco. Spodnja meja takega zaporedja je enaka prvemu členu: .
Aritmetično zaporedje je torej navzdol omejeno, ko je naraščajoče ali konstantno. V tem primeru je spodnja meja .
Zaporedje je omejeno, kadar je navzgor in navzdol omejeno.
Aritmetično zaporedje je omejeno, ko je hkrati naraščajoče in hkrati padajoče. Edina aritmetična zaporedja, ki ustrezajo obema zahtevama, so konstantna zaporedja.
Aritmetična sredina - naloga
Gotovo si se že srečal z aritmetično sredino.
Ali znaš izračunati aritmetično sredino števil in ?
Kaj pa aritmetično sredino števil in ?
In aritmetična sredina števil in ?
Na vprašanj-e/i si odgovoril pravilno.
Aritmetična sredina
Oglejmo si aritmetično zaporedje: , , , , ... in zapišimo nekaj njegovih začetnih členov. Pobliže si oglejmo šesti člen zaporedja, ki je enak , in opazujmo, kolikšna je aritmetična sredina njemu simetrično ležečih členov:
Naj bo poljuben člen aritmetičnega zaporedja. Izračunajmo aritmetično sredino njegovega predhodnika in naslednika.
.
Aritmetična sredina
Do enakega rezultata bi prišli tudi v primeru, ko bi od poljubnega člena šli za dva člena nazaj in dva naprej ter izračunali njuno aritmetično sredino.
In če gremo od -tega člena za členov naprej in nazaj?
Izračunajmo aritmetično sredino – tega in – tega člena.

Najprej izračunajmo vsakega posebej.
Izračunajmo njuno aritmetično sredino.
Ugotovili smo naslednje:
Naloga
Poišči , da bo zaporedje s členi , , aritmetično. Na koncu zaporedje še zapiši.
Ti je uspelo? Preveri rezultat.
x =
Iskan je enak , zaporedje pa tvorijo členi , , .
Namig:
Uporabi prejšnjo ugotovitev, da je drugi člen enak aritmetični sredini prvega in tretjega.
Zveza med poljubnima členoma aritmetičnega zaporedja
Dobil si sistem dveh enačb z dvema neznankama, ki ga rešiš tako, da recimo od druge enačbe odšteješ prvo in dobiš:
Sedaj je potrebno le še izračunati prvi člen.
Poskusi še enkrat.
Poskusi sam priti do rešitve tako, da in izraziš s prvim členom in diferenco ter enega od njiju izračunaš.
Zveza med poljubnima členoma aritmetičnega zaporedja
Podobno poiščemo zvezo med -tim in -tim členom aritmetičnega zaporedja.
Zapišemo -ti in -ti člen zaporedja:
Odštejmo prvo enakost od druge.
V aritmetičnem zaporedju za poljubni naravni števili in velja: .
Linearna interpolacija
Med števili in želiš vriniti števil tako, da bodo skupaj s prvim številom in zadnjim številom tvorila aritmetično zaporedje. Katera števila je treba vriniti? Položaj je takšen:

Dobili bomo torej -členo zaporedje, pri čemer bo in . Izračunajmo diferenco:
Zapišimo zaporedje: , , , , , , , , .
Interpolacija je računanje vrednosti funkcije v kaki točki na intervalu, če so znane njene vrednosti na koncih intervala.
Linearna interpolacija
Spodnja animacija prikazuje še grafično ponazoritev linearne interpolacije.
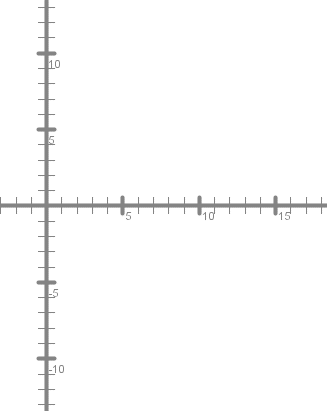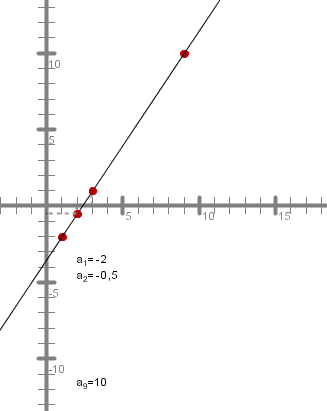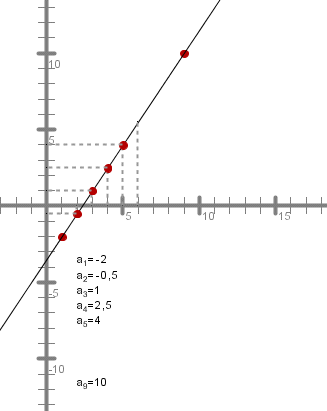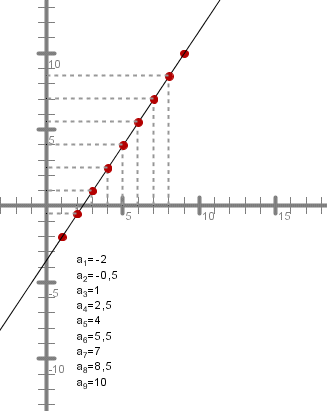
Denimo, da imamo števili in , med kateri želimo vriniti členov, da bodo le-ti (skupaj z in ) tvorili aritmetično zaporedje.
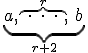
Torej velja: , . Izračunajmo diferenco tega zaporedja.
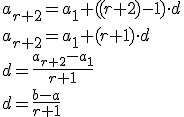
Dodatne naloge
| , | |
| , | |
| , | |
| , | , |
Narobe. Poskusi ponovno.
| , , | in |
| , , | |
| ,, | in |
| , , |
Narobe. Poskusi ponovno.
Sedmi člen aritmetičnega zaporedja je enak , diferenca pa . Izračunaj, od katerega člena naprej so členi tega zaporedja pozitivni.
Členi zaporedja so pozitivni od . člena naprej.
Členi zaporedja so pozitivni od 16. člena naprej.
Narobe. Poskusi ponovno.
Šesti člen aritmetičnega zaporedja je enak , deseti pa . Kateri člen tega zaporedja je enak ? (Odgovor zapiši s številko.)
. člen zaporedja je enak .
Narobe. Poskusi ponovno.
Med števili in vrinemo števil tako, da dobimo aritmetično zaporedje. Izračunaj splošni člen zaporedja.
narobe. Poskusi ponovno.
Koliko je števil, večjih od in manjših od , ki dajo pri deljenju s številom ostanek ?
Takih števil je .
Narobe. Poskusi ponovno.
Stranice trikotnika s ploščino in obsegom tvorijo aritmetično zaporedje. Koliko merijo stranice tega trikotnika?
a = dm, b = dm,
c = dm
a=dm,
b=dm in
c=dm
Narobe. Poskusi ponovno.
Rezultati