Ponovitev aritmetičnega in geometrijskega zaporedja.
1. Dano zaporedje , , , ... je:
2. Dano zaporedje , , , ... je:
Ponovitev AZ in GZ
Na drugo vprašanje si odgovoril narobe.
Na prvo vprašanje si odgovoril narobe.
Na obe vprašanji si odgovoril narobe.
Poglej količnik in razliko med sosednjimi členi.
Ponovitev AZ in GZ
Spomnimo se kako izračunamo splošni člen in vsoto prvih členov aritmetičnega in geometrijskega zaporedja.
Poveži!
V aritmetičnem zaporedju je razlika dveh zaporednih členov vedno enaka, označimo jo z .
V geometrijskem zaporedju pa je količnik dveh zaporednih členov vedno enak, označimo ga s .
| aritmetično zaporedje | ||
| geometrijsko zaporedje |
Poskusi ponovno.
Ponovitev AZ in GZ
Ponovimo še lastnost za geometrijsko in aritmetično sredino prvih treh členov v aritmetičnem in geometrijskem zaporedju.
Preizkusi svoje znanje in na spodaj poveži pravilni zvezi.
Poskusi ponovno.
Preizkusi se
Preberi spodnji stavek in ga dopolni.
Pri aritmetičnem zaporedju je drugi člen sredina prvega in tretjega člena.
Poskusi ponovno.
Primeri
Ogledali si bomo tri različne primere, kjer nastopata geometrijski in aritmetični zaporedji skupaj.
1. primer
Če seštejemo prvih deset členov aritmetičnega zaporedja, dobimo vsoto . Četrti, šesti in deveti člen tega zaporedja sestavljajo geometrijsko zaporedje. Zapiši obe zaporedji.
Zapišimo podatke, ki jih poznamo.
Imamo aritmetično zaporedje:, , , ,... s prvim členom in diferenco .
Vemo, da je in, da členi , , tvorijo novo geometrijsko zaporedje.
Začnimo najprej z drugim podatkom in zapišimo po splošnem členu aritmetičnega zaporedja četrti, šesti in deveti člen , , .
Vemo, da nam ti členi določajo geometrijsko zaporedje:
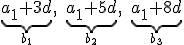
1. primer
Uporabimo geometrijsko sredino za prve tri člene geometrijskega zaporedja: ,
vstavimo naše podatke: ,
poračunamo: ,
združimo podobne člene: ,
izpostavimo diferenco .
Od tod imamo za dve možnosti: in .
Dobili smo dve rešitvi. To ne pomeni nujno, da smo dobili dve zaporedji, izračunati moramo še prvi člen.
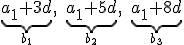
1. primer
Izračunati še moramo prvi člen aritmetičnega zaporedja, zato uporabimo še prvi podatek in zapišimo vsoto prvih desetih členov aritmetičnega zap.: .
1. Obravnavajmo najprej prvo možnost . Vstavimo torej v podatke najprej za in dobimo: ,
seštejemo in zmnožimo, dobimo: ,
izrazimo prvi člen: .
Sedaj poznamo prvi člen in diferenco aritmetičnega zaporedja zato lahko zaporedje zapišemo.
Zapiši to zaporedje.
Aritmetično zaporedje: , , , , , , , , , ...
, , , , , , , , ,
1. primer
Aritmetično zaporedje: , , , , , , , , ,
Geometrijsko zaporedje: , ,
Poglej si namig.
Zapišemo četrti, šesti in deveti člen aritmetičnega zaporedja.
Geometrijsko zaporedje: , , ,...
Aritmetično zaporedje se začne s členom in ima diferenco .
Geometrijsko zaporedje je enako četrtemu, šestemu in devetemu členu aritmetičnega zaporedja.
2. primer
Naslednjo nalogo poskusi rešiti sam. Če se povsem zatakne, si pomagaj z rešitvijo pod gumbom. V vsakem primeru pa čimveč premislekov poskusi izpeljati sam.
Vsota prvih treh členov geometriskega zaporedja je . Če prvi člen povečamo za , drugega ne spreminjamo, tretjega pa zmanjšamo za , dobimo aritmetično zaporedje. Katera števila sestavljajo aritmetično zaporedje?
Aritmetično zaporedje sestavljajo števila
Še enkrat poskusi. Pomagaj si z rešitvijo.
Najprej izpišimo podatke.
Vemo, da je vsota prvih treh členov geometrijskega zaporedja .
Zato zapišimo formulo za vsoto prvih členov: ,
vstavimo podatke, razstavimo in okrajšamo:
ter izrazimo prvi člen: .
Imamo podano tudi geometrijsko zaporedje s prvim členom in količnikom .
Zato zaporedje vemo, da če prvi člen povečamo za ena: , drugega pustimo in ga izrazimo s prvim členom in količnikom , tretjega pa zmanjšamo za tri ter ga izrazimo s prvim členom in količnikom: , dobimo novo zaporedje:
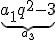
ki je aritmetično.
Uporabimo aritmetično sredino za prve tri člene aritmetičnega zaporedja: ,
vstavimo naše podatke: in odpravimo ulomek: ,
sedaj vstavimo prvi člen , ki smo ga zgoraj izrazili: ,
odpravimo ulomke, ter združimo podobne člene: ,
rešimo kvadratno enačbo in dobimo dve rešitvi: in .
Vstavimo obe rešitvi v izražen prvi člen in dobimo: in .
Zapišemo prve tri člene obeh zaporedij.
1. Za in
Geometrijsko zaporedje: , ,
Aritmetično zaporedje : , ,
2. Za in
Geometrijsko zaporedje: , ,
Aritmetično zaporedje: , ,
3. primer
Koliko so stari bratci na sliki in kako velike čevlje nosijo?

|
3. primer: Pot do rešitve
Trije bratci so se rodili istega meseca. Njihovo starost nam predstavljajo trije zaporedni členi geometrijskega zaporedja. Številke njihovih čevljev pa zaporedne člene aritmetičnega zaporedja. Najstarejši bratec ima številko čevljev šestkrat večjo od števila let. Drugi bratec ima številko čevljev . Razlika med št. čevljev in starostjo najmlajšega bratca je , razlika med št. čevljev in starostjo pri drugih dveh bratcih pa je enaka. Izračunaj starosti in številke čevljev naših bratcev.
Najprej si zapišimo obe zaporedji:
Starosti bratcev nam predstavljajo geometrijsko zaporedje (leta): , ,
Številke čevljev pa nam predstavljajo aritmetično zaporedje: , , .
Zapišimo zveze med podatki iz teksta naloge.
Drugi bratec ima št. čevljev , kar pomeni, da je drugi člen v aritmetičnem zaporedju , to zapišemo: , izrazimo prvi člen: in ga vstavimo v člene aritmetičnega zaporedja.
Dobimo aritmetično zaporedje z neznano diferenco: .
3. primer: Pot do rešitve
Najmlajši bratec ima razliko med št. čevljev in starostjo , to zapišemo: ,
iz te enačbe izrazimo diferenco: .
Najstarejši bratec ima št. čevljev šestkrat večjo od starosti, kar pomeni: ,
vstavimo diferenco in izrazimo prvi člen: .
Razlika med št. čevljev in starostjo pri starejših bratcih je enaka: .
Poenostavimo enačbo, vstavimo diferenco in prvi člen: ,
odpravimo ulomke in poenostavimo, dobimo: ,
izračunamo diskriminanto: .
Po formuli za kvadratno enačbo dobimo rešitvi: in
Vstavimo količnik v izražen prvi člen in dobimo: in , ki ni rešitev, ker ni naravno število.
Vstavimo še prvi člen v izraženo diferenco in dobimo: .
Sedaj lahko zapišemo obe zaporedji.
Leta: ,,
Št. čevljev: ,,
Poskusi sam!
Sestavi nalogo, ki bo zajemala aritmetično in geometrijsko zaporedje hkrati in jo tudi reši.
Izmisli si neko aritmetično ali geometrijsko zaporedje in ga zapiši, nato nekaterim danim členom spremeni vrednost tako, da bodo določala člene drugega zaporedja. Naprej ni več težko! Če ne gre, glej zgornje naloge od zadaj naprej!
Za določitev aritmetičnega zaporedja sta potrebna dva podatka, prvi člen in diferenca, zato potrebujemo dve enačbi s tema dvema neznankama.
Podobno velja tudi za geometrijsko zaporedje, če poznamo prvi člen in količnik, je zaporedje enolično določeno, zato tudi tukaj potrebujemo dve enačbi s tema dvema neznankama.
Dodatne naloge
Aritmetično zaporedje: , , ,
Geometrijsko zaporedje: , ,
Aritmetično zaporedje je pravilno, geometrijsko pa ne.
Geometrijsko zaporedje je pravilno, aritmetično pa ne.
Obe zaporedji sta napačni.
Dodatne naloge
Vsota prvih treh členov padajočega aritmetičnega zaporedja je , vsota prvih treh členov naraščajočega geometrijskega zaporedja pa . Prvi člen geometrijskega zaporedja je tretji člen aritmetičnega zaporedja. Tretji člen geometrijskega zaporedja pa je prvi člen aritmetičnega zaporedja. Zapiši obe zaporedji.
Aritmetično zaporedje: , ,
Geometrijsko zaporedje: , ,
Pravilno si ugotovil.
Aritmetično zaporedje: , ,
Geometrijsko zaporedje: , ,
Aritmetično zaporedje je pravilno, geometrijsko pa ne.
Geometrijsko zaporedje je pravilno, aritmetično pa ne.
Obe zaporedji sta napačni.
Dodatne naloge
Poskusi ponovno.
Dodatne naloge
Poskusi ponovno.
Dodatne naloge
Starosti vnuka, mame in babice predstavljajo prve tri člene aritmetičnega zaporedja. Vnuk in babica sta skupaj stara pol stoletja. Starosti vnuka, vnukinje in babice pa predstavljajo prve tri člene geometrijskega zaporedja. Zapiši aritmetično in geometrijsko zaporedje, če veš, da sta bratec in sestrica skupaj stara let.
Aritmetično zaporedje: , ,
Geometrijsko zaporedje: , ,
Pravilno si ugotovil.
Aritmetično zaporedje je pravilno, geometrijsko pa ne.
Geometrijsko zaporedje je pravilno, aritmetično pa ne.
Obe zaporedji sta napačni.