Pritisnite F11

Iz varnostnih razlogov je mogoče celozaslonski način vključiti samo s pritiskom na gumb F11 na tipkovnici.

Ko ste enkrat v celozaslonskem načinu, ga izključite spet s pritiskom na F11.

Potenčna funkcija

Avtor: E-um (vsebinsko), Skupina NAUK (tehnično)

Sodelujoče organizacije

Izvedbo projekta je omogočilo sofinanciranje Evropskega socialnega sklada Evropske unije in Ministrstva za šolstvo in šport. Pri tehnični izvedbi projekta so sodelovali: Fakulteta za matematiko in fiziko Univerze v Ljubljani, Inštitut za matematiko, fiziko in mehaniko in podjetje Hruška d.o.o.

Hvala za ogled gradiva!

Veseli bomo vaših komentarjev. Obiščite nas na www.nauk.si.

Uporabljeni viri

E-um

www.e-um.si

Sodelujoče organizacije

Izvedbo projekta je omogočilo sofinanciranje Evropskega socialnega sklada Evropske unije in Ministrstva za šolstvo in šport. Pri tehnični izvedbi projekta so sodelovali: Fakulteta za matematiko in fiziko Univerze v Ljubljani, Inštitut za matematiko, fiziko in mehaniko in podjetje Hruška d.o.o.

Razmislek

Spoznavali bomo torej funkcije oblike $f(x)= x^n, n \in \mathbb{Z}$ . Če dobro razmisliš, ugotoviš, da dve potenčni funkciji že poznaš. Kateri?

Odgovor

Znanje bomo razširili na poljubne cele eksponente.

Ker bomo imeli (po imenu sodeč) kar precej dela s potencami, je dobro ponoviti pravila za računanje s potencami.

Pravila za računanje s potencami

Poznamo funkciji $g(x)=x^0$ in $f(x)=x^1$ , ki sta posebna primera že dobro znane linearne funkcije. Tukaj bomo govorili o funkcijah, kjer bo potenca $|n|>1$ .

$a^na^m=a^{n+m}$ $(a^n)^m = a^{nm}$ $(ab)^n = a^nb^n$ $a^0=1$ $a^{-1} = \frac{1}{a^n}$ $a ^{\frac {n}{m}}= \sqrt [m]{n}$

Potenčna funkcija z naravnim sodim eksponentom

Potenčna funkcija z naravnim eksponentom je funkcija s predpisom $f(x)=x^n$ , kjer je $n \in \mathbb{N}$ .

Na sliki lahko spreminjaš vrednost $n$ , torej eksponent potenčne funkcije. Ob tem se ti izrisuje ustrezen graf. Spreminjaj $n$ in opazuj, kako to vpliva na obliko grafa.

Aplikacija RiŠ se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)

Riš datoteka

Poskusi sam
Pri spreminjanju eksponenta opaziš, da dobimo dve različni skupini grafov. Glede na kaj bi jih razdelili?

Odgovor

Naj bo $n=2$ . Kaj je v tem primeru definicijsko območje in kaj zaloga vrednosti?

Odgovor

Primerjaj svoj odgovor za $n=4$ oziroma $n=6$ .

Odgovor

Pri katerih vrednostih spremenljivke $x$ dosežejo vse potenčne funkcije s sodim eksponentom isto vrednost?

Odgovor

Kaj pa opaziš pri vrednosti funkcije za pozitivne oziroma za negativne $x$ ?

Odgovor

Ali imajo inverzno funkcijo?

Odgovor

Kaj se dogaja z obliko grafa v okolici ničle oziroma za velike $x$ , kadar eksponent postaja vse večji?

Odgovor

Opazimo, da imajo grafi s sodim eksponentom podobno obliko; prav tako grafi z lihim eksponentom.

$D_f = \mathbb {R}$ $Z_f = [ 0, \infty )$

Potenčne funkcije s sodim eksponentom dosežejo isto vrednost pri $x=1$ , $x=0$ in $x=–1$ , torej vse potekajo skozi točke $(1, 1)$ , $(0, 0)$ in $(–1, 1)$ .

Potenčne funkcije s sodim eksponentom so:

sode, saj je $f(–x)=f(x)$ ,

naraščajoče za $x>0$ in padajoče za $x<0$ .

Inverzne funkcije nimajo, ker niso bijektivne.

Graf se v okolici ničle vse bolj "lepi" k osi $x$ , z večanjem (oziroma manjšanjem) vrednosti $x$ pa vrednosti funkcije zelo naraščajo; čim večji je eksponent, tem strmejši je graf.

Lastnosti potenčnih funkcij z naravnim sodim eksponentom

Zapišimo povzetek vseh ugotovitev za potenčno funkcijo z naravnim sodim eksponentom.

Lastnosti potenčnih funkcij $f(x)=x^n$ z naravnim sodim eksponentom:

definicijsko območje so vsa realna števila, zaloga vrednosti pa nenegativna realna števila;

grafi potekajo skozi tri skupne točke $A(1,1)$ , $B(-1,1)$ in $O(0,0)$ ;

imajo eno ničlo pri $x=0$ :

so padajoče za $x<0$ in naraščajoče za $x>0$ ;

so navzdol omejene;

grafi so zrcalni glede na ordinatno os; torej so funkcije sode;

niso bijektivne.

Grafi potenčnih funkcij z naravnim sodim eksponentom

Potenčne funkcije z naravnim lihim eksponentom

Poskusi sam

Podrobno si spoznal potenčne funkcije s sodim naravnim eksponentom. Razišči še drugo skupino, tj. potenčne funkcije z naravnim lihim eksponentom.
Skozi katere skupne točke potekajo grafi potenčnih funkcij z lihim eksponentom?

Odgovor

Ali so te funkcije realne funkcije?

Odgovor

Ali obstajata točki na grafu, ki imata enaki funkcijski vrednosti? Kaj lahko sklepaš?

Odgovor

Kaj lahko rečemo o legi grafa v I. kvadrantu glede na graf v III. kvadrantu? Katero lastnost imajo take funkcije?

Odgovor

V čem se razlikujejo grafi funkcij, ko večamo lihi eksponent?

Odgovor

Grafi se sekajo v treh točkah, v koordinatnem izhodišču, točki $(1, 1)$ in $(–1, –1)$ .

Funkcije so realne, če sta tako definicijsko območje kot zaloga vrednosti (pod) množica realnih števil. To za potenčne funkcije z naravnim lihim eksponentom velja, torej so realne funkcije.

Vse točke na grafu imajo različne koordinate $y$ , kar pomeni, da je funkcija bijektivna.

Vidimo, da sta si dela grafa zrcalna glede na koordinatno izhodišče, kar je lastnost lihih funkcij oziroma $f(-x)= - f(x)$ .

Grafi funkcij z večanjem eksponenta vse hitreje naraščajo; v bližini koordinatnega izhodišča pa so vse bolj "prilepljeni" na os $x$ .

Grafi potenčnih funkcij z naravnim lihim eksponentom

Poglej si na sliki spodaj grafe različnih potenčnih funkcij z naravnim lihim eksponentom.

Lastnosti potenčnih funkcij z naravnim lihim eksponentom

Potenčne funkcije f(x)=x^n z lihim naravnim eksponentom:

- $D_f = Z_f = \mathbb {R}$ ;

grafi potekajo skozi tri skupne točke $A(1, 1)$ , $B(–1, –1)$ in $O(0, 0)$ ;

imajo eno ničlo pri $x=0$ ;

so povsod naraščajoče;

neomejene;

lihe; grafi so zrcalni glede na koordinatno izhodišče;

bijektivne.

Potenčne funkcije z negativnim celim eksponentom

Postal si že pravi mojster za potenčne funkcije. Sedaj boš svoje znanje razširil na potenčne funkcije $f(x)=x^n$ z negativnim celim eksponentom, kjer je $n \in \mathbb{Z}^{-}$ .

Na sliki spodaj lahko spreminjaš vrednost eksponenta. Ob tem se ti izrisuje ustrezen graf potenčne funkcije.

Aplikacija RiŠ se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)

Riš datoteka

Poskusi sam

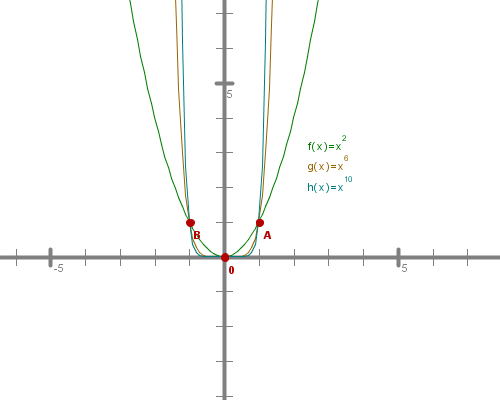
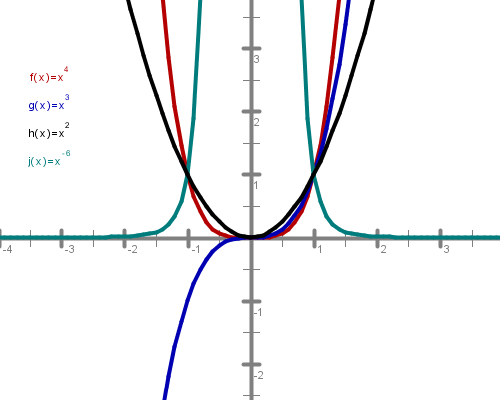
Najprej opazuj oblike grafov pri spreminjanju eksponenta od $–1$ do $–7$ .

Kaj se dogaja z grafi funkcij v bližini koordinatnega izhodišča? Zakaj?

Odgovor

Vidimo, da se grafi funkcij v okolici koordinatnega izhodišča zelo strmo dvigajo in približujejo k ordinatni osi, ki je nikoli ne dosežejo. Pravimo, da imajo funkcije pri $x=0$ pol, ker tam niso definirane.

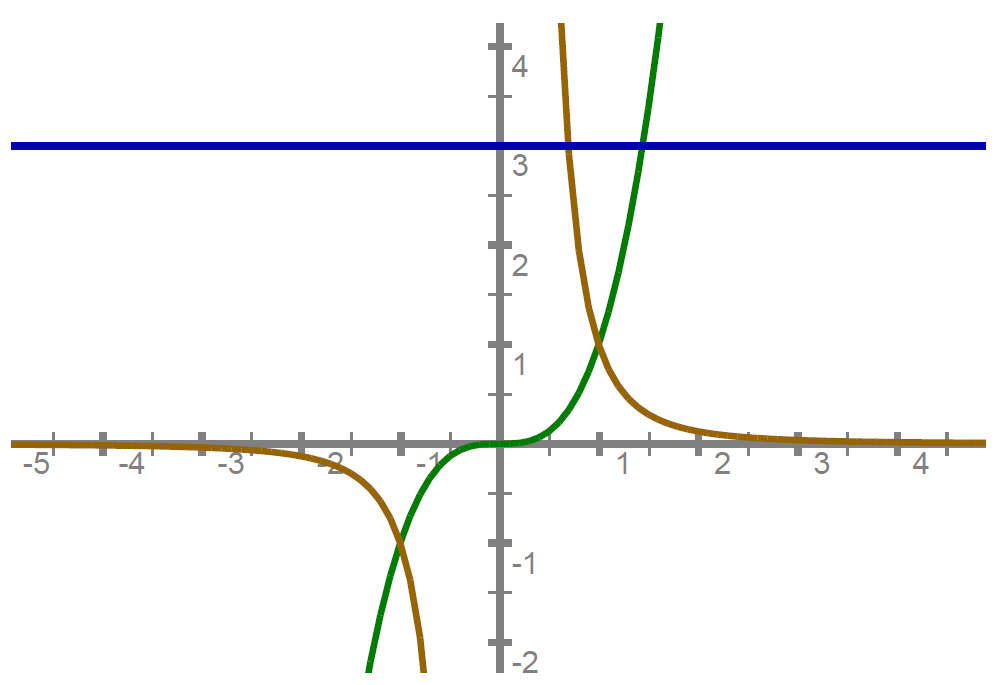
Opazuj, kaj se dogaja z vrednostmi funkcij, daleč oddaljenih stran od koordinatnega izhodišča.

Odgovor

Pri naravnih eksponentih smo ugotovili, da imamo dve skupini potečnih funkcij v odvisnosti od eksponenta. Ali kaj podobnega velja tudi tukaj?

Odgovor

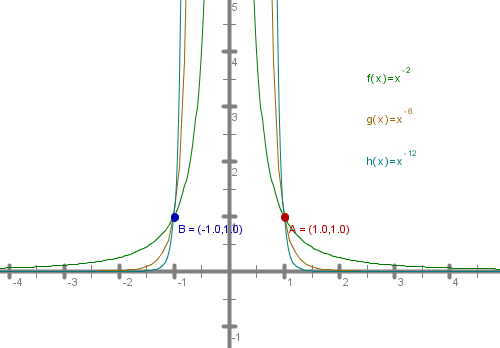
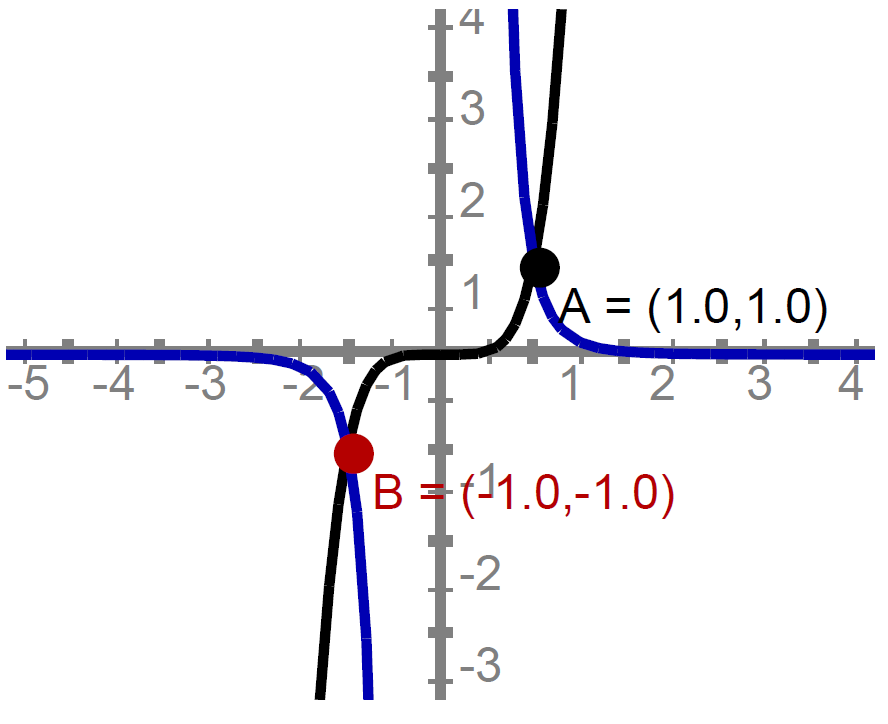
Opazuj grafe funkcij z negativnim sodim eksponentom. Katere skupne lastnosti opaziš?

Namig

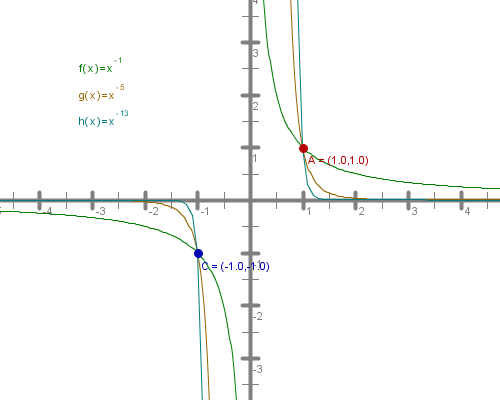
V katerih lastnostih se razlikujejo grafi potenčnih funkcij z negativnim sodim eksponentom od tistih z lihim eksponentom?

Odgovor

Ker je sedaj potenčna funkcija z negativnim celim eksponentom, jih lahko zapišemo tudi kot $f(x)= x^{-1}= \frac{1}{x^n}, n \in \mathbb {N}$ . Ulomki niso definirani, kadar je imenovalec enak $0$ . Imenovalec je vse manjši (vse bliže $0$ ), torej je njegova obratna vrednost vse večja.

Čim večja je vrednost $x$ , tem manjša je vrednost $\frac{1}{x^n}$ . Torej so grafi daleč od izhodišča približujejo abscisni osi in je nikoli ne dosežejo. Pravimo, da je abscisna os asimptota teh funkcij.

Delitev je enaka; ločimo potenčne funkcije z negativnim lihim oziroma sodim eksponentom.

Pomagaj si z opazovanimi lastnostmi pri potenčnih funkcijah z naravnim eksponentom.

Grafi potenčnih funkcij z negativnim sodim eksponentom so zrcalni glede na ordinatno os (torej so funkcije sode); grafi potenčnih funkcij z negativnim lihim eksponentom so zrcalni glede na koordinatno izhodišče.

Grafi potenčnih funkcij z negativnim sodim eksponentom za $x<0$ naraščajo, za $x>0$ pa padajo; grafi potenčnih funkcij z negativnim lihim eksponentom so povsod padajoči.

Grafi potenčnih funkcij z negativnim sodim eksponentom imajo dve skupni točki $A(1, 1)$ in $B(–1, 1)$ ; grafi potenčnih funkcij z negativnim lihim eksponentom pa točki $A(1, 1)$ in $C(–1, –1)$ .

Potenčne funkcije z negativnim sodim eksponentom niso injektivne; potenčne funkcije z negativnim lihim eksponetom so bijektivne.

Lastnosti funkcij z negativnim sodim eksponentom

Da boš imel boljši pregled nad svojim pridobljenim znanjem o potenčnih funkcijah z negativnim celim eksponentom, si še enkrat preberi njihove lastnosti in oglej grafe posameznih funkcij.

Lastnosti funkcij z negativnim sodim eksponentom:

$D_f = \mathbb{R}- \{0\};$

$Z_f = \mathbb{R}^{0};$

grafi potekajo skozi dve skupni točki $A(1, 1)$ in $B(–1, 1)$ ;

imajo pol pri $x=0$ (os $y$ je navpična asimptota);

os $x$ je vodoravna asimptota;

so navzdol omejene;

nimajo ničel;

so padajoče za $x>0$ in naraščajoče za $x<0$ ;

so sode funkcije;

niso bijektivne.

Grafi potenčnih funkcij z negativnim sodim eksponentom

Iz slike se vidi, kako se spreminja strmina grafov v odvisnosti od eksponenta potenčne funkcije.

Lastnosti funkcij z negativnim lihim eksponentom

Lastnosti potenčnih funkcij z negativnim lihim eksponentom:

$D_f = Z_f = \mathbb{R}- \{0\};$

grafi potekajo skozi dve skupni točki $A(1, 1)$ in $C(–1, –1)$ ;

imajo pol pri $x=0$ ;

os $x$ je vodoravna asimptota, ki je nikjer ne sekajo;

so povsod padajoče;

so neomejene;

grafi so zrcalni glede na koordinatno izhodišče; torej so funkcije lihe;

so bijektivne.

Grafi potenčnih funkcij z negativnim lihim eksponentom

Grafi funkcij se skoraj "prilepijo" ob os $x$ .

Naloga 1

Pazljivo preberi trditve spodaj in ugotovi, ali so pravilne ali nepravilne.
1. Vse potenčne funkcije so definirane na množici vseh realnih števil. Pravilno. Napačno.

2. Vse potenčne funkcije potekajo skozi točko (1, 1). Pravilno. Napačno.

3. Potenčne funkcije z lihimi eksponenti imajo inverzne funkcije. Pravilno. Napačno.

Namig

4. Grafi potenčnih funkcij so zrcalni glede na koordinatno izhodišče. Pravilno. Napačno.

Pazi

Preveri

Pravilno

Bravo. Na vsa vprašanja si odgovoril pravilno.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.

Inverzne funkcije imajo samo funkcije, ki so bijektivne.

Trditev velja samo za potenčne funkcije z lihim eksponentom.

Naloga 2

Zapiši predpis potenčne funkcije $f$ , ki poteka skozi točko $A(–2, \frac{1}{16})$ .

Rešitev

V kateri točki se seka graf dobljene funkcije z grafom funkcije $g(x)=x^3$ ?

Rešitev

Za katere vrednosti $x$ je graf funkcije $f$ nad grafom funkcije $h(x)=x^2$ ?

Kaj pa za funkcijo $j(x)=x^{–6}$ ?

Grafi funkcij

Nariši grafe funkcije $f(x)$ , $g(x)$ , $h(x)$ in $j(x)$ v isti koordinatni sistem.

Rešitev

Potenčna funkcija $f(x)=x^n$ bo določena, ko bomo poznali njen eksponent.

$f(–2)=16–1$ $(–2)n=16^{–1}=(–2)^{–4},$

torej je $n=–4$ .
Iskana potenčna funkcija je $f(x)=x^{–4}$ .

$A(1, 1)$

S slike spodaj ali z računa lahko ugotoviš, da se funkciji sekata v točkah $(–1 ,1)$ in $(1, 1)$ in je $f(x)>h(x)$ za $–1<x<1$ .

Pri funkciji $j$ zahtevano velja za $x<–1$ in $x>1$ .

Naloga 3

Napiši predpis potenčne funkcije, če:

Funkcija zavzame vrednost $16$ pri $x = 2$ ;

Točka $A(−3,− \frac{1}{27} )$ leži na grafu funkcije;

Ima funkcija pol pri $x = 0$ in je soda funkcija;

Je zrcalna glede na koordinatno izhodišče in poteka skozi točko $B(x, 125)$ (možna sta dva odgovora).

Počisti

$f(x)= x^4$

$g(x)= x^{-3}$

$f(x)= x^{-2n}$ , kjer je $n \in \mathbb{N}$

$f(x)= x^3$

$f(x)= x^2$

$f(x)= x^{-2}$

$f(x)= x^{-3n}$ , kjer je $n \in \mathbb{N}$

Preveri

Pravilno

Pravilno si povezal izraze, ki so enaki.

Napačno

Mogoče je, da so nekateri izmed tvojih ujemanj pravilni, vendar ne vsi. Poskusi še enkrat.

Naloga 4

Dani imaš funkciji $f(x) = x^5$ in $g(x) = x^{−5}$ .
a) Nariši grafa funkcij.
b) Računsko in grafično poišči njune presečne točke.
c) Zapiši intervale, na katerih je $f(x) < g(x)$ .
d) Zapiši predpisa za njuni inverzni funkciji.

a)

Grafi funkcij

b)Presečišči sta A (1, ), B(-1, )
c)Ti intervali so: $x<$ in $<x<$
d)Njuni inverzni funkciji sta:

$f^{-1}(c)=x^{-5}$ in $g^{-1}(x)= x^5$

$f^{-1}(c)=-x^5$ in $g^{-1}(x)= -x^{-5}$

$f^{-1}(c)=\frac{1}{x^5}$ in $g^{-1}(x)= \frac{1}{x^{-5}}$

$f^{-1}(c)=\sqrt[5]{x}$ in $g^{-1}(x)= \sqrt[5]{x^{-1}}$

Preveri

Pravilno

Bravo. Na vsa vprašanja si odgovoril pravilno.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.

Naloga 5

Nariši lik, ki ga omejujeta krivulji $y = x^{−3}$ , $y = x^3$ in premica $y = 3$ . Zapiši oglišča dobljenega lika.

a)

Grafi funkcij

b) Oglišča dobljenega lika so:

$A(1,1), B(\sqrt[3]{3^{-1}},3), C(\sqrt{3},3)$

$A(-1,1), B(\sqrt[3]{3^{-1}},3), C(\sqrt[3]{3},3)$

$A(1,1), B(\sqrt{3^{-1}},3), C(\sqrt[3]{3},3)$

$A(1,1), B(\sqrt[3]{3^{-1}},3), C(\sqrt[3]{3},3)$

Preveri

Pravilno

Bravo. Na vsa vprašanja si odgovoril pravilno.

Napačno

Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.

Potenčna funkcija

Vaš brskalnik je zastarel

Pritisnite F11

Potenčna funkcija

Avtor: E-um (vsebinsko), Skupina NAUK (tehnično)

Sodelujoče organizacije

Hvala za ogled gradiva!

Veseli bomo vaših komentarjev. Obiščite nas na www.nauk.si.

Uporabljeni viri

Sodelujoče organizacije

Pravilno

Napačno

Pravilno

Napačno

Pravilno

Napačno

Pravilno

Napačno