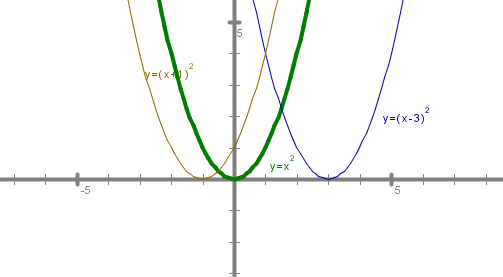
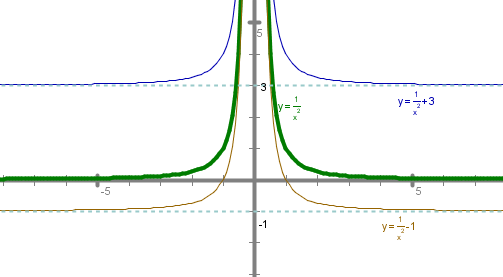
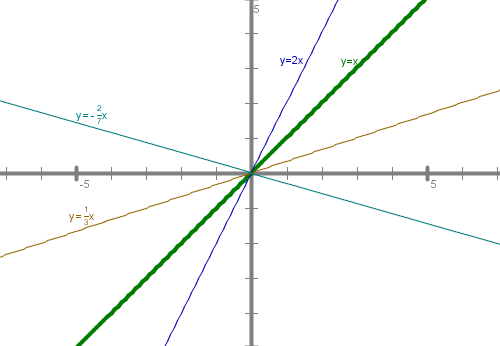
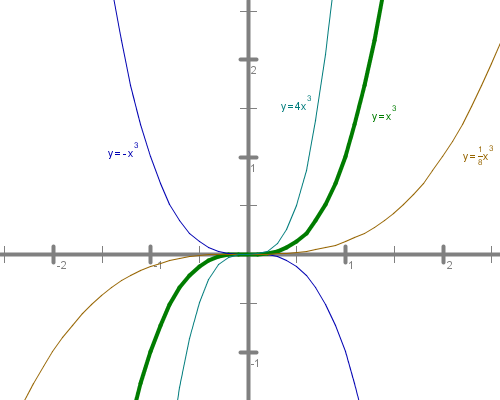
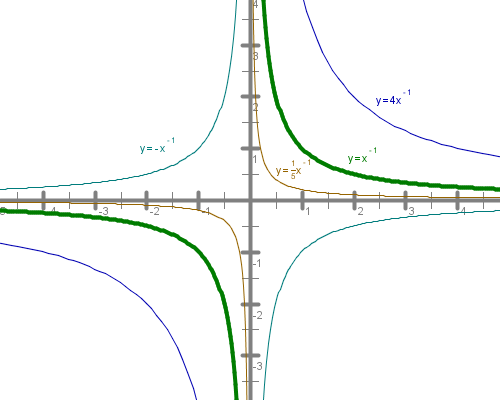
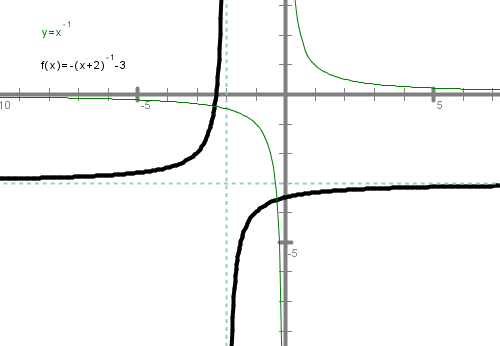
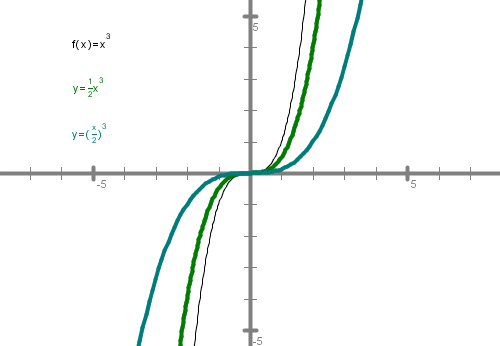
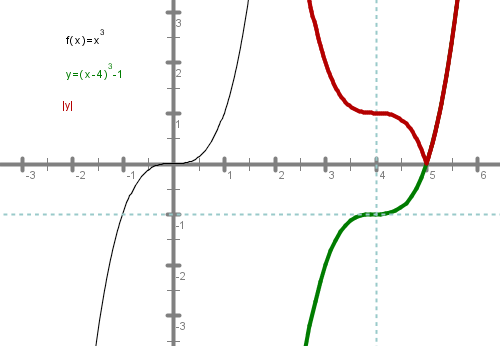
Najprej se bomo spomnili preslikav množic točk v ravnini. Predlagam, da si pri vsaki nalogi pomagaš s sliko. Vse slike rešitev imaš na koncu vseh nalog.
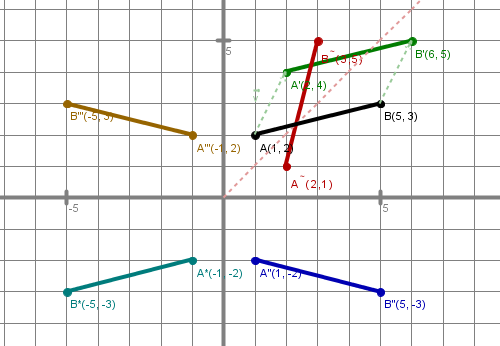
Ukvarjali se bomo z daljico s krajiščema in . Nariši jo v koordinatni sistem. 1. Premakni daljico za vektor . Kje ima premaknjena daljica krajišči? Kako bi ju izračunal? Opiši to preslikavo.
| Odgovor |
2. Prezrcali daljico preko abscisne osi in zapiši koordinati krajišč prezrcaljene daljice. Kaj se pri zrcaljenju preko abscisne osi zgodi s posamezno točko?
| Odgovor |
3. Kam se preslikata krajišči, če daljico AB prezrcalimo preko ordinatne osi? Opiši to zrcaljenje.
| Odgovor |
4. Preslikaj sedaj še daljico AB preko koordinatnega izhodišča in zapiši njene nove koordinate. Kaj se zgodi s posamezno točko pri tej preslikavi?
| Odgovor |
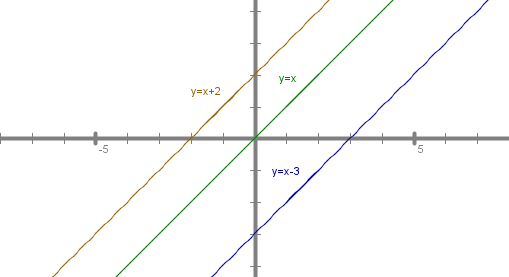
5. Razmisli, kam se preslikata krajišči daljice AB, če jo prezrcališ preko simetrale lihih kvadrantov (premice y = x).
| Odgovor |
| Slike rešitev |
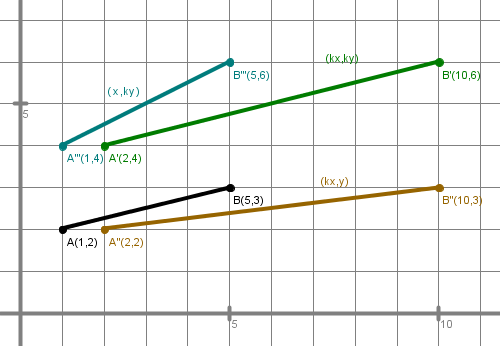
Raziščimo še preslikave, pri katerih se dolžina ne ohranja. Vse naloge se še vedno nanašajo na prej podano daljico s krajišči in . Pri reševanju si pomagaj s slikami; njihove rešitve najdeš na koncu celotnega sklopa nalog. 1. Vsako koordinato krajišče daljice pomnoži z . Kaj se zgodi z dolžino daljice in z njeno lego?
| Odgovor |
2. Kako imenujemo to preslikavo?
| Odgovor |
3. Če pomnožimo s faktorjem samo koordinato točke, govorimo o raztegu v smeri abscisne osi.
Če pomnožimo s faktorjem samo ordinato točke, pa govorimo o raztegu v smeri osi .
Izračunaj koordinati krajišč za oba raztega za faktor in nariši sliki raztegnjenih daljic.
| Slike rešitev raztegov daljice |