Zgodovinsko gledano so se prvi zametki misli o kompleksnih številih pojavili tedaj, ko so matematiki (ter fiziki in filozofi ...) naleteli na kvadratni koren iz negativnega števila (npr. ), ki so ga sicer razlagali kot "nesmiselni rezultat" ali zgolj fiktivni pripomoček, so pa z njegovo uporabo rešili kakšen problem.
Vpeljava in predstavitev kompleksnih števil
Razlogi za vpeljavo kompleksnih števil
Zgled 1
Pravilno
Bravo. Na vsa vprašanja si odgovoril pravilno.
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi.
Preberi si rešitev.
- (a) ,
- (b) Enačba nima realnih rešitev.
Te enačbe še ne znamo rešiti, saj dobimo , pri čemer vemo, da je kvadrat poljubnega realnega števila vedno nenegativno realno število, kar se lepo vidi tudi z grafa funkcije .
Zgled 2
Girolamo Cardano (1501–1576) je – ob posredni pomoči svojih predhodnikov – izpeljal znamenito Cardanovo formulo, s katero je podal eksplicitni zapis rešitve enačbe tretje stopnje (ta enačba ima pravzaprav tri rešitve):
Ko je reševal enačbo , je z uporabo zgornje formule dobil rešitev
v kateri dobimo pod korenom negativno število in naravni sklep za tedanjega matematika in pa srednješolca do te ure bi bil, da enačba pač nima realnih rešitev. No, z nekaj več znanja bi lahko pokazali, da je vrednost tega izraza enaka , kar je po svoje presenetljivo: z uporabo kvadratnega korena iz negativnega števila smo prišli do realne rešitve. Poglejmo še zgled, ki bo nekoliko bliže našemu dosedanjemu znanju in ga bomo brez težav razumeli, sporočilo pa bo enako: s "čudnim računanjem" s kvadratnimi koreni iz negativnih števil bomo prišli do realne rešitve.
Zgled 3
Teme parabole določi tako, da njegovo absciso izračunaš kot aritmetično sredino ničel:
(to je eden izmed načinov, ki smo ga spoznali pri poglavju o kvadratni funkciji). Teme je:
| Namig |
Na obeh prejšnjih zgledih lahko jasno vidimo, da nas včasih tudi uporaba navidezno nemogočih objektov pripelje k čisto lepi rešitvi. Ker pa smo pri vseh treh primerih ugotovili, da se vedno znova vračamo h kvadratnemu korenu iz negativnega števila, pri čemer je njegova uporaba celo smiselna (kot smo videli v zgledih 2 in 3), je napočil čas, da vpeljemo novo številsko množico, ki bo kot nova števila zaobjela tudi vse kvadratne korene iz negativnih realnih števil.
| Preveri |
Pravilno
Bravo. Tvoj odgovor je pravilen.
Napačno
Tvoj odgovor je napačen. Poskusi še enkrat.
Izračunajmo presečišči parabole z abscisno osjo:
Rešitvi seveda nista realni, zato parabola nima presečišč za abscisno osjo. Pa za hipec pozabimo na "čudni zapis" in izračunajmo absciso temena po znani formuli:
Vidimo, da se "čudni del" odšteje in lahko nanj pozabimo, končni rezultat pa je realno število. Če izračunamo še ordinato temena, dobimo teme.
Vpeljava kompleksnih števil
Pri zgledih smo ugotovili, da v množici realnih števil ne znamo rešiti kvadratne enačbe .
Pa se dogovorimo, da nam bo to enačbo rešilo posebno (zaenkrat še nekoliko skrivnostno) število, ki ga bomo označili z . Zanj bo torej veljalo . Temu novemu številu dajmo tudi ime:
Premisli: Takoj se bomo prepričali, da je vpeljava takšnega novega števila smiselna in uporabna. Kako lahko sedaj s pomočjo novega števila zapišemo kvadratni koren iz poljubnega negativnega realnega števila?
| Odgovor je skrit tukaj |
Spoznali smo že enega predstavnika nove številske množice − število , nismo pa še povedali nič o tem, kakšne oblike so števila v tej novi številski množici.
V zgornjem zgledu smo videli, da je lahko število pomnoženo s poljubnim realnim številom , torej so lahko tudi števila elementi nove številske množice (na primer: , itd.). Če tem številom prištejemo še neko realno število , dobimo spet novo število oblike (pri čemer izraza ne moremo bolj skrčiti iz podobnih razlogov kot pri računanju z izrazi: in sta objekta različne vrste). Tako dobimo recimo števila , ... To spoznanje bomo povzeli v nadeljevanju.
Najprej si poglejmo uporabnost novega števila na konkretnem zgledu: izračunajmo .
Zaenkrat ne vemo, katero število je to, zato ga označimo z :
Na zgornji zapis lahko pogledamo tudi nekoliko drugače, če obe strani skvadriramo:
Rešujemo torej podobno enačbo, kot v primeru . Preoblikujmo zgornjo enačbo in upoštevajmo lastnost novega števila :
Od tod pa lahko s primerjanjem obeh strani sklepamo, da je , torej je .
Ves postopek računanja bi lahko torej poenostavljeno zapisali kot:
Sedaj lahko zapišemo tudi splošno ugotovitev o računanju kvadratnega korena iz negativnega realnega števila:
kjer je .
Množica kompleksnih števil
Množica kompleksnih števil je številska množica, ki vsebuje vsa števila oblike
kjer sta in poljubni realni števili, pa imaginarna enota. Zapišimo to še s simboli:
| Zahtevnejša utemeljitev številske množice |
Kompleksna števila običajno označujemo tudi s črkami , ... ali pa (redkeje) z grškimi črkami , ..., torej kot
Pri tem imenujemo realno število realni del kompleksnega števila in označimo kot , realno število pa imaginarni del kompleksnega števila in označimo kot .
Utemeljitev dobre opredelitve takšne nove številske množice bomo v celoti razumeli po vpeljavi računskih operacij na množici kompleksnih števil, sedaj pa nakažimo le dva ključna premisleka.
Množica kompleksnih števil mora biti zaprta za seštevanje in množenje, to pomeni, da mora biti vsota poljubnih dveh kompleksnih števil spet kompleksno število (t. j. oblike ), enako pa mora veljati tudi za množenje. Čeprav seštevanja in množenja na kompleksnih številih še nismo spoznali, bomo ti dve računski operaciji v tem dokazu uporabili intuitivno.
(a) Zaprtost seštevanja
Naj bosta in poljubni kompleksni števili, kjer so , , in realna števila. Seštejmo ju na "naravni način", kot to počnemo z običajnimi algebrskimi izrazi (dvočleniki), ko seštevamo člene "iste vrste":
Po preureditvi smo dobili obliko, kot je značilna za kompleksna števila: izraza in sta namreč spet realni števili (vemo: vsota realnih števil je realno število) in v drugem delu nastopa produkt z imaginarno enoto . Torej je vsota dveh kompleksnih števil spet kompleksno število.
(b) Zaprtost množenja
Naj bosta znova in poljubni kompleksni števili, kjer so , , in realna števila. Zmnožimo ju na "naravni način", kot to počnemo z običajnimi algebrskimi izrazi (dvočleniki), pri čemer upoštevamo samo eno novo spoznanje, da je namreč :
Dobljeni izraz je seveda nekoliko bolj zapleten kot pri seštevanju, vendar je razmislek analogen: izraza in sta namreč spet realni števili (vemo: vsota, razlika in produkt realnih števil je spet realno število) in v drugem delu nastopa produkt z imaginarno enoto . Torej je produkt dveh kompleksnih števil spet kompleksno število.
Preveri svoje razumevanje
Z odgovori na spodnja vprašanja lahko preveriš svoje razumevanje pravkar vpeljanih novih pojmov.
1. V kakšni zvezi sta novo vpeljana množica kompleksnih števil in množica realnih števil, ki smo jo poznali do sedaj? Ali lahko zapišemo poljubno realno število v obliki kompleksnega števila?
| Namig |
2. Kako lahko zapišemo poljuben kvadratni koren iz negativnega realnega števila v obliki kompleksnega števila?
3. Zapiši nekaj primerov čistih imaginarnih števil.
4. Določi realni in imaginarni del kompleksnega števila .
,
.
5. Izračunaj ničli kvadratne funkcije . Kaj opaziš?
| Namig |
| Preveri |
Pravilno
Bravo. Na vsa vprašanja si odgovoril pravilno.
Res je:
- Vsako realno število je tudi kompleksno število oblike in obratno.
Velja torej: natanko tedaj, ko je realno število. - Poljuben kvadratni koren iz negativnega realnega števila lahko zapišemo kot in števila te oblike imenujemo čista imaginarna števila.
Velja torej: natanko tedaj, ko je z čisto imaginarno število ali . - Čista imaginarna števila so:
- Če je , je , .
- Ničli kvadratne funkcije sta Opazimo, da ima kvadratna funkcija v primeru negativne diskriminante dve kompleksni ničli, ki ju sedaj že znamo izračunati.
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi.
Preberi si rešitev.
Rešitev:
- Vsako realno število je tudi kompleksno število oblike in obratno.
Velja torej: natanko tedaj, ko je realno število. - Poljuben kvadratni koren iz negativnega realnega števila lahko zapišemo kot in števila te oblike imenujemo čista imaginarna števila.
Velja torej: natanko tedaj, ko je z čisto imaginarno število ali . - Čista imaginarna števila so:
- Če je , je , .
- Ničli kvadratne funkcije sta Opazimo, da ima kvadratna funkcija v primeru negativne diskriminante dve kompleksni ničli, ki ju sedaj že znamo izračunati.
Množica realnih števil je podmnožica kompleksnih števil:
Naprej izračunaj sam.
Grafična predstavitev kompleksnih števil
Kako lahko grafično predstavimo kompleksna števila?
Z realnimi števili nimamo težav, saj vemo, da vsaki točki na številski premici pripada natanko eno realno število in obratno. Kako pa predstaviti število oblike ? Ker je vsako kompleksno število sestavljeno iz dveh komponent (realnega in imaginarnega dela), se človeku pojavi samoumevna misel, da lahko tako število predstavimo le v dvodimenzionalnem prostoru. Pomislimo torej na ravnino in na pravokotni koordinatni sistem (to seveda ni tako "naravno" in samoumevno, kot smo zapisali, sicer matematiki v zgodovini ne bi potrebovali toliko časa za vpeljavo tega koncepta).
Res, opišimo ravnino, v kateri bomo grafično predstavili kompleksna števila.
Predstavitev kompleksnih števil v kompleksni ravnini
S premikanjem kompleksnega števila v ravnini lahko opazuješ spreminjanje realnega dela in imaginarnega dela števila .
Posebej si oglej zapis realnih števil na realni osi in čistih imaginarnih števil na imaginarni osi.
|
| Riš datoteka |
Podobno kot pri kartezičnem koordinatnem sistemu v Evklidski ravnini lahko tudi tukaj zapišemo ugotovitev:
Utemeljitev tega dejstva je popolnoma enaka kot pri prirejanju koordinat (urejenega para števil in ) poljubni točki v Evklidski ravnini.
Iz zgoraj zapisane ugotovitve pa sledi še en zanimiv zapis (predstavitev) kompleksnih števil:
Kompleksno število lahko zapišemo tudi v obliki , torej
Zgled 4
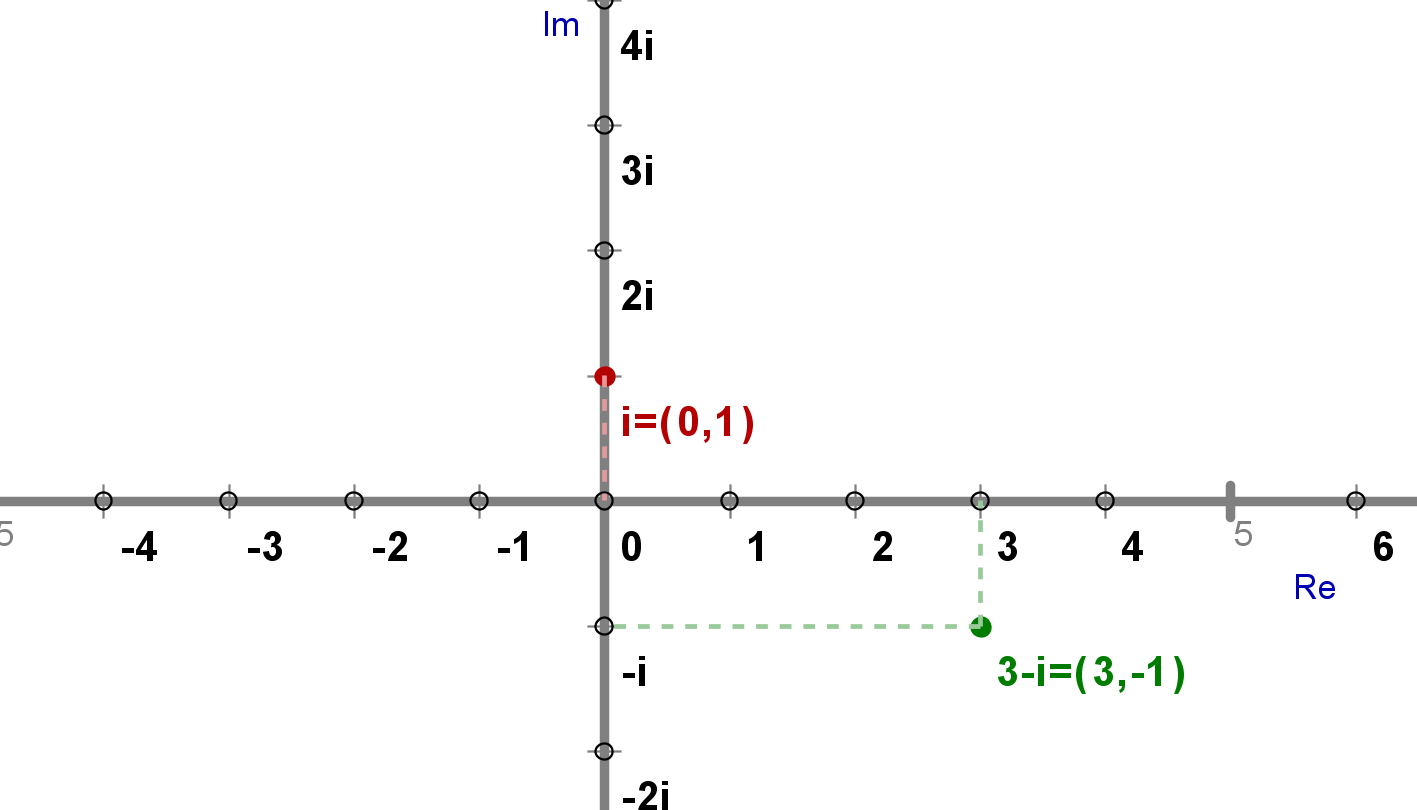
Kompleksni števili in lahko zapišemo tudi kot oziroma in ju predstavimo v kompleksni ravnini kot:
Dodatek za radovedne - iz preteklosti v sedanjost
Leonhard Euler (1707-1783) je izpeljal nekaj najpomembnejših zvez in lastnosti kompleksnih števil – ena zanimivejših je
kjer so v eni enačbi povezane tri pomembne matematične konstante. Euler še ni uporabljal poimenovanja kompleksna števila.
Pariški knjigarnar J. R. Argand je leta 1806 prvi predlagal predstavitev kompleksnih števil v kompleksni ravnini (ki bi se zato morala imenovati vsaj Argand-Gaussova ravnina), ime kompleksna števila in (vnovično) zamisel kompleksne ravnine pa je leta 1831 dokončno vpeljal veliki matematik Carl Friedrich Gauss (1777–1855).
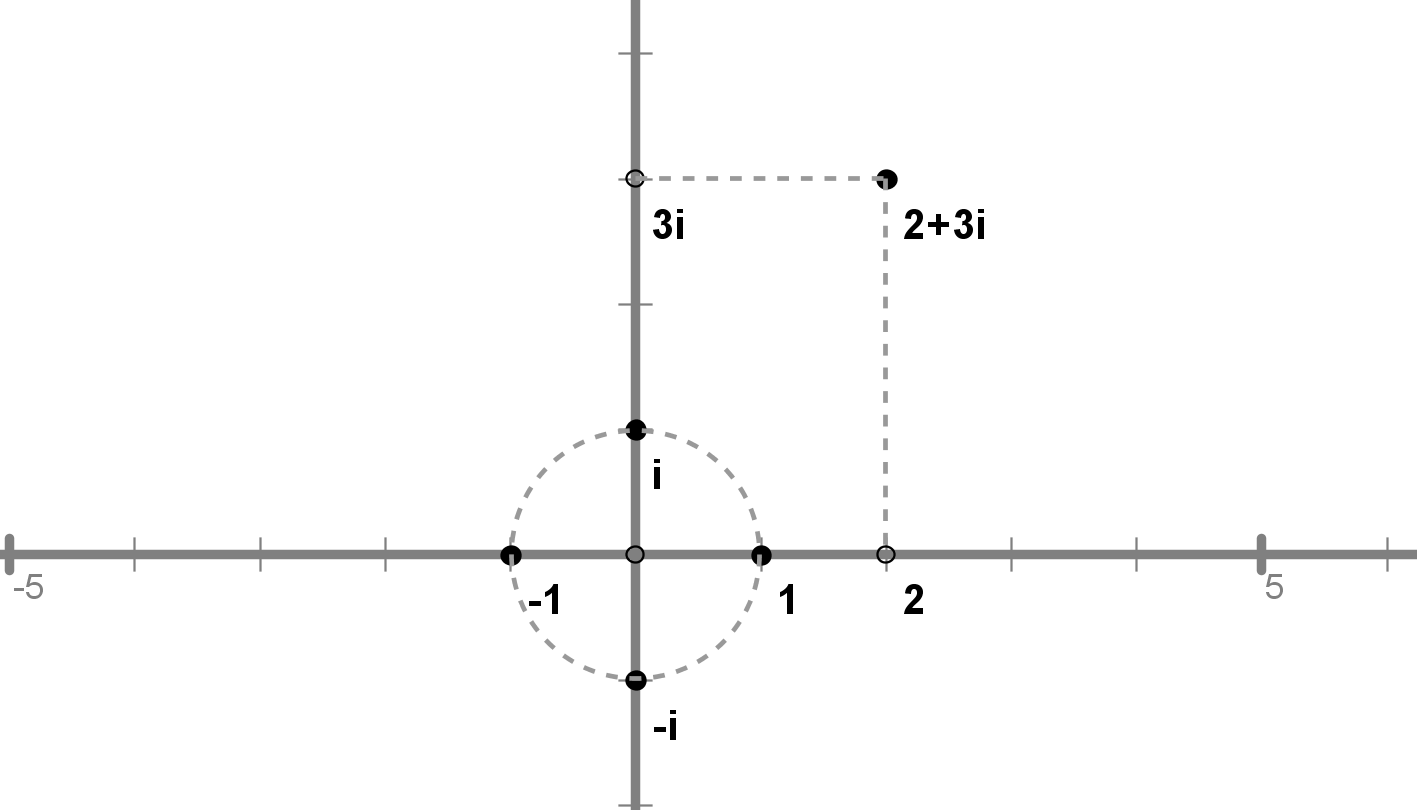
Slika prikazuje Argandovo idejo predstavitve "fiktivnih" ali "monstruoznih" imaginarnih števil: točka s koordinatama pripada kompleksnemu številu . Kasnejši razvoj teorije kompleksnih števil je pripeljal do razvoja mnogih teoretičnih in uporabnih področij matematike, ki se še danes skokovito razvijajo. Poleg tega so se kompleksna števila izkazala kot odličen pripomoček pri reševanju zahtevnih problemov na področju geometrije, elektrotehnike (fizike) in še kje.
Naloga 1
Ponovi, katere računske operacije so definirane na množicah , , in .
Na množicah so definirane:
| Preveri |
Pravilno
Pravilno si povezal izraze, ki so enaki.Napačno
Mogoče je, da so nekateri izmed tvojih ujemanj pravilni, vendar ne vsi. Poskusi še enkrat.Napačno
Mogoče je, da so nekateri izmed tvojih ujemanj pravilni, vendar ne vsi.
Preberi si rešitev.
Rešitev:
- Na množici sta definirani (notranji) operaciji seštevanje in množenje, na množici seštevanje, odštevanje in množenje, na množicah in pa seštevanje, odštevanje in množenje ter deljenje z neničelnimi števili.
Naloga 2
Pravilno
Bravo. Na vsa vprašanja si odgovoril pravilno.
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Preberi si rešitev.
Rešitev:
Naloga 3
Pravilno
Bravo. Na vsa vprašanja si odgovoril pravilno. Tu pa je podana še grafična rešitev: predstavitev kompleksnih števil.
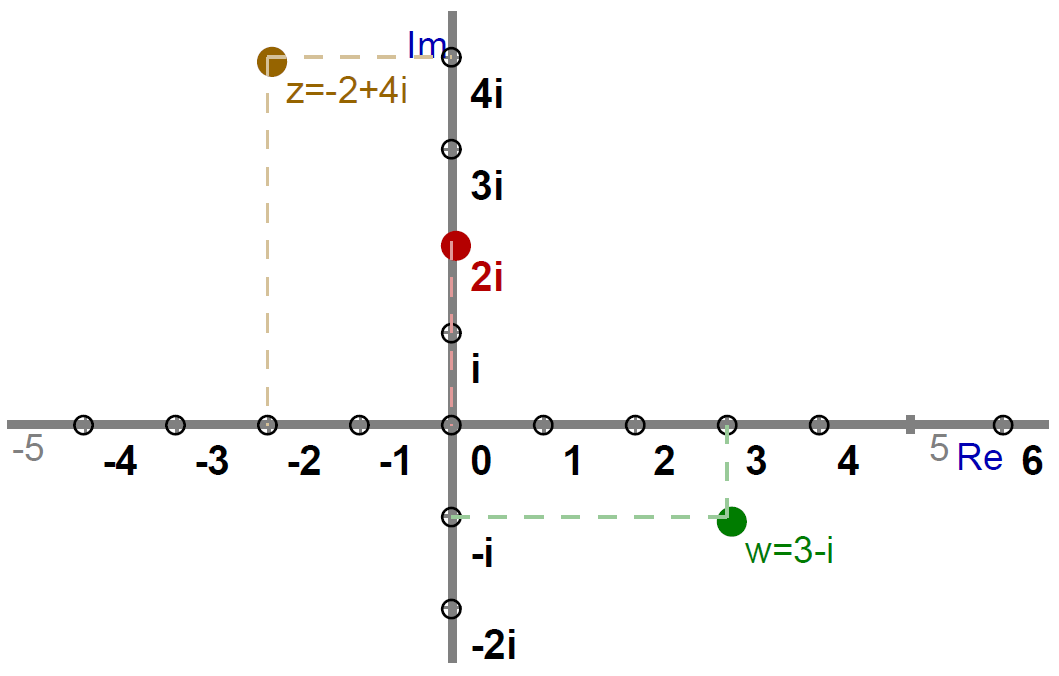
Na sliki so kompleksna števila , in .
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Poskusi še enkrat.
Napačno
Nekateri tvoji odgovori so lahko pravilni, vendar ne vsi. Preberi si rešitev.
Rešitev:
- ,
- in
.

Naloga 4
Pravilno
Bravo. Tvoj odgovor je pravilen.
Napačno
Tvoj odgovor je napačen. Poskusi še enkrat.
Rezultati
- Razlogi za vpeljavo kompleksnih števil
- Zgled 1
- Zgled 2
- Zgled 3
- Vpeljava kompleksnih števil
- Množica kompleksnih števil
- Preveri svoje razumevanje
- Grafična predstavitev kompleksnih števil
- Predstavitev kompleksnih števil v kompleksni ravnini
- Zgled 4
- Dodatek za radovedne - iz preteklosti v sedanjost
- Naloga 1
- Naloga 2
- Naloga 3
- Naloga 4
- Rezultati