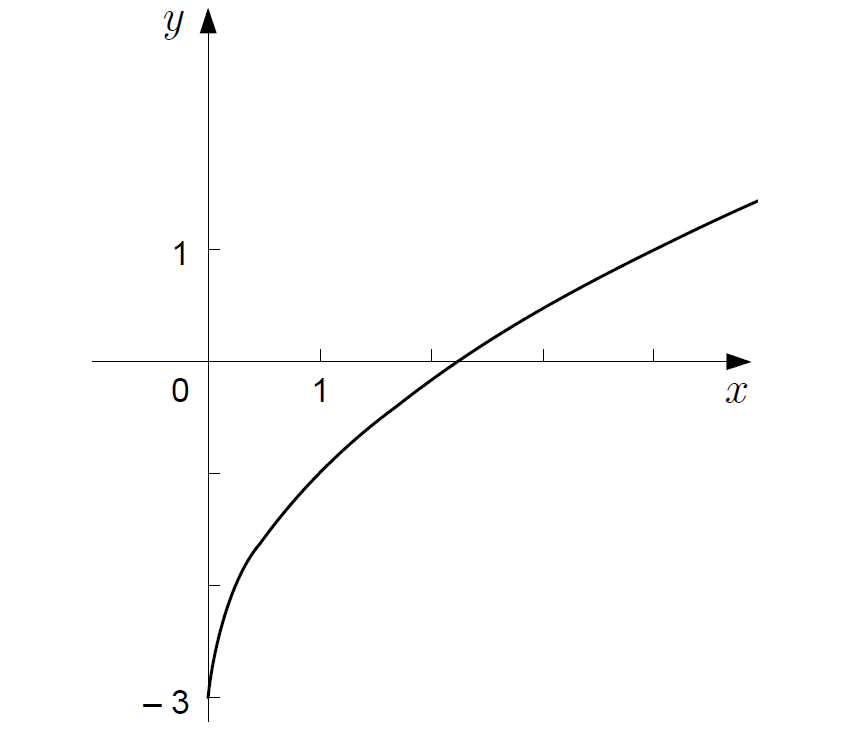Naloga 1
Dana je funkcija .
a) Narišite graf funkcije . Zapišite definicijsko območje in zalogo vrednosti funkcije ter izračunajte njeno ničlo.
b) V točki položimo normalo na krivuljo . Napišite enačbo te normale.
c) Naj bo , pri čemer je . Določite tako, da bo ploščina lika med grafom funkcije in osjo na intervalu enaka .
d) Naj bo , pri čemer je . Določite tako, da bo ploščina lika med grafom funkcije , osjo in osjo enaka .
Rešitev: Naloga 1
a)
Graf funkcije :
Zapis definicijskega območja: .
Zapis zaloge vrednosti: .
Izračunana ničla: .
b)
Izračunan odvod: .
Izračunan smerni koeficient: .
Zapis ali uporaba formule: .
Zapisana enačba normale: .
c)
Zapisana enačba: .
Zapisan rezultat: .
d)
Zapisana enačba: .
Zapisan rezultat: .
Naloga 2
Dana je geometrijska vrsta , , .
a) Za katera realna števila je ta vrsta konvergentna?
b) Izračunajte število , za katero je vsota te vrste enaka .
c) Naj bo . Koliko odstotkov vsote vseh členov te vrste predstavlja vsota prvih petih členov? Rezultat zaokrožite na mest.
d) Naj bo . Kateri členi te vrste so manjši od ? Napišite odgovor.
Rešitev: Naloga 2
a)
Ugotovitev: , .
b)
Zapis ali uporaba formule: .
Rešitvi enačbe in .
Ugotovitev, da ne ustreza.
c)
Izračunana ali uporabljena vsota vrste: .
Zapis vsote prvih petih členov: .
Izračunan odstotek:
d)
Zapisana neenačba: .
Rešitev neenačbe: .
Odgovor: »Vsi členi od vključno dvanajstega naprej.«
Naloga 3
Rešite naslednje naloge iz trigonometrije.
a) Dokažite, da za trikotnik na sliki velja .
b) Izračunajte dolžino stranice v trikotniku s podatki , in (poiščite obe možni rešitvi).
c) Izračunajte natančno vrednost , če sta in kota na spodnji sliki, dolžine daljic so , in , daljici in pa sta pravokotni.
Rešitev: Naloga 3
a)
Uporaba sinusnega izreka: .
Upoštevanje .
b)
1. način:
Uporaba kosinusnega izreka za stranico .
Ureditev kvadratne enačbe: , .
Rešitvi: in .
2. način:
Izračun obeh vrednosti kotov in : , in , .
Uporabi sinusnega ali kosinusnega izreka za izračun stranice .
Rešitvi: in .
c)
1. način:
Uporaba adicijskega izreka.
,
,
Rezultat:
2. način:
Uporaba kosinusnega izreka za kot
Izračun stranic trikotnika , ,
