Pritisnite F11

Iz varnostnih razlogov je mogoče celozaslonski način vključiti samo s pritiskom na gumb F11 na tipkovnici.

Ko ste enkrat v celozaslonskem načinu, ga izključite spet s pritiskom na F11.

Limita funkcije

Avtor: E-um (vsebinsko), Skupina NAUK (tehnično)

Sodelujoče organizacije

Izvedbo projekta je omogočilo sofinanciranje Evropskega socialnega sklada Evropske unije in Ministrstva za šolstvo in šport. Pri tehnični izvedbi projekta so sodelovali: Fakulteta za matematiko in fiziko Univerze v Ljubljani, Inštitut za matematiko, fiziko in mehaniko in podjetje Hruška d.o.o.

Hvala za ogled gradiva!

Veseli bomo vaših komentarjev. Obiščite nas na www.nauk.si.

Uporabljeni viri

E-um

www.e-um.si

Sodelujoče organizacije

Izvedbo projekta je omogočilo sofinanciranje Evropskega socialnega sklada Evropske unije in Ministrstva za šolstvo in šport. Pri tehnični izvedbi projekta so sodelovali: Fakulteta za matematiko in fiziko Univerze v Ljubljani, Inštitut za matematiko, fiziko in mehaniko in podjetje Hruška d.o.o.

Včasih ni čisto jasno, kakšno vrednost ima funkcija za določen $x=a$ , ali pa v tej točki funkcija sploh ni definirana. Limita funkcije pa je takšno število, ki so mu vrednosti funkcije zelo blizu, ko se $x$ bliža dani točki $a$ .

Primer

Oglejmo si malo neobičajno, a zanimivo realno funkcijo s predpisom:
$f(x)=(\frac{1}{2})^{(\frac{1}{|x|})}$ .

Opazovali jo bomo v okolici točke $x=0$ . V tej točki funkcija ni definirana, saj tam ni definirana funkcija $g(x)=\frac{1}{|x|}$ .

Vprašamo se: "Kako se spreminjajo funkcijske vrednosti $f(x)$ , ko se z $x$ bližamo točki $0$ ?" ali "Kaj se s funkcijo dogaja v okolici točke $x=0$ ?"

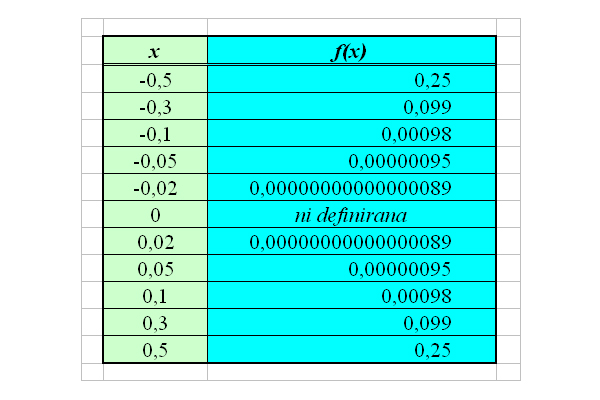
Pomagajmo si s tabelo 1 na naslednji strani.

Primer

Tabela 1: Vrednosti funkcije f(x) v bližini točke x=0.

Iz tabele lahko sklepamo: "Ko se $x$ bliža k $0$ , tako z negativne kot s pozitivne strani, se zdi, da so vrednosti funkcije vse bolj podobne $0$ , se torej bližajo $0$ ."

Splošno

Imejmo neko funkcijo $f(x)$ , ki je definirana na neki okolici točke $a$ , razen morda v sami točki $a$ . Opazujemo, kaj se dogaja z vrednostmi funkcije $f(x)$ , ko se $x$ približuje točki $a$ . Če se te vrednosti funkcije bližajo (limitirajo) neki konkretni (eni sami) vrednosti $b$ , pravimo, da je $b$ limita funkcije $f(x)$ , ko se $x$ približuje točki $a$ .

To je preprosta opredelitev pojma limita, sledila bo kar naporna matematična definicija, vendar nikar ne obupaj, vztrajaj. Trud je vedno poplačan.

Zapis za limito funkcije, ko se $x$ približuje točki $a$ , je

$\lim_{x \to a}f(x)$

Kako beremo oznako?

Zapis

$\lim_{x \to a}f(x)=b$

običajno preberemo takole:

"Limita funkcije $f(x)$ , ko gre $x$ proti $a$ , je enaka $b$ ."

Limita v primeru

V primeru, s katerim smo začeli, bi rekli, da vrednosti funkcije limitirajo k $0$ . Tako bi lahko zapisali:

$\lim_{x \to 0}f(x)=0$

ali

$\lim_{x \to 0}(\frac{1}{2})^{(\frac{1}{|x|})}$

.

Kako pa natančno matematično vemo, da je točka $b$ res limita funkcije $f(x)$ , ko se $x$ približuje točki $a$ ?

Dogovorimo se:

Število $b$ je limita funkcije $f(x)$ , ko se $x$ približuje točki $a$ , če za vsako pozitivno število $\epsilon$ obstaja tako pozitivno število $\delta$ , da velja: če je $x$ v $\delta$ -okolici točke $a$ in $x \neq a$ , je $f(x)$ v $\epsilon$ -okolici števila $b$ .

Krajše zapisano

$\lim_{x \to a}f(x)=b,$

če za vsak $\epsilon>0$ obstaja tak $\delta$ , da velja: $(|x–a|<\delta)Λ(x \neq a) \Longrightarrow |f(x)–b|<\epsilon$ .

Obstoj limite

Obstoj limite v točki $x=a$ funkcije $f(x)$ na gibljivi sliki

Na sliki lahko z miško spreminjaš lego točke na drsniku. To točko lahko potiskaš gor in dol, pri tem pa spreminjaš velikost $\epsilon$ -okolice točke $b$ .

V tem primeru je število $b$ limita funkcije na sliki, ko se $x$ približuje točki $a$ . Za vsak izbran $\epsilon$ namreč obstaja tak $\delta$ , da je za vsak $x$ iz $\delta$ -okolice točke $a$ vrednost $f(x)$ v $\epsilon$ -okolici točke $b$ . Za vsak $x$ iz vsake (zelene) $\delta$ -okolice točke $a$ so res vrednosti funkcije $f(x)$ v (modri) $\epsilon$ -okolici točke $b$ . Na sliki se izriše največja obstoječa $\delta$ -okolica točke $a$ za izbrani $\epsilon$ .

Aplikacija RiŠ se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)

Riš datoteka

Imaš probleme z uporabo slike?

Za premikanje točke na drsniku z miško pritisneš in z levim gumbom držiš ter vlečeš točko, označeno s črno karo.

Poskusi, lažje boš razumel.

Obstoj limite

Tudi na spodnji sliki s premikanjem drsnika spreminjaš velikost $\epsilon$ .

Da bi bila točka $b$ limita funkcije, ko se $x$ približuje $a$ , bi za vsak izbor $\epsilon$ (še tako majhen) morala obstajati $\delta$ -okolica točke $a$ , da bi za vsak $x$ iz te okolice vrednost $f(x)$ bila v $\epsilon$ -okolici točke $b$ . Vendar ko $\epsilon$ dovolj zmanjšamo, $\delta$ -okolica točke $a$ izgine, ne obstaja. To pomeni, da $b$ ni limita funkcije na sliki, ko se $x$ približuje k $a$ .

Če bi pogledali poljubno $\delta$ -okolico točke $a$ , potem ko na sliki (zelena) $\delta$ -okolica izgine, bi ugotovili naslednje: če vzameš kateri koli $x$ z desne polovice poljubne $\delta$ -okolice točke $a$ , se ta preslika (nad vrednost $c: f(x)>c$ ) zunaj $\epsilon$ -okolice točke $b$ (modra). Kar pomeni, da ta vrednost ni v bližini vrednosti $b$ , kar pa je v nasprotju z bistvom limite.

Poskusi na sliki.

Aplikacija RiŠ se ni mogla zagnati. Prosim preverite, ali imate v brskalniku namescen program Java 1.4.2 (ali novejsi) (Kliknite tu za namestitev Jave)

Riš datoteka

Izkaže se, da limita te funkcije v točki $a$ sploh ne obstaja. Preprostejša razlaga: ko se bližamo točki $a$ z leve strani, se vrednosti funkcije $f(x)$ bližajo $b$ , tako bi bila limita število $b$ . Ko se bližamo k $a$ z desne, pa se funkcijske vrednosti bližajo vrednosti $c$ in bi zato morala biti limita število $c$ . Limita pa je lahko samo ena, tako ni nobena od izbir $b$ ali $c$ primerna oz. pravilna. Če bi si izbrali katero koli drugo število za limito, bi obstajal $\epsilon$ , za katerega ne bi obstajal potreben $\delta$ , tako kot se zgodi za število $b$ na zgornji sliki. Poskusi.

Primer

Vzemimo pod drobnogled naslednjo realno funkcijo realne spremenljivke z deljenim predpisom (te so namreč zanimivejše kot preproste elementarne funkcije, ki nas glede limite ne morejo zares presenetiti):

$f(x)=\begin{cases} x+2; & x<1\\ 2;& x=1\\ -x+2;& x>1. \end{cases}$

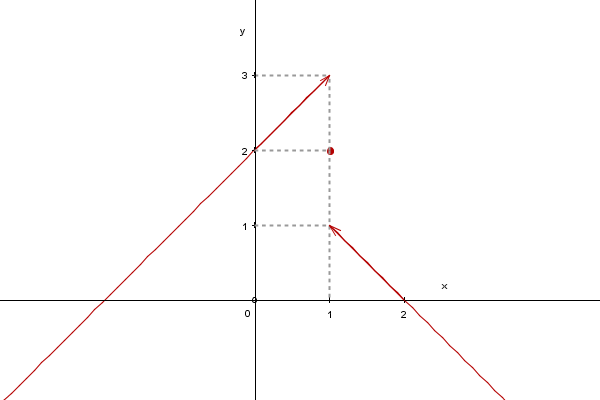
Pomagali si bomo z grafom te funkcije:

Graf funkcije f(x)

Preizkusi se

Preuči graf, tako boš lažje odgovoril na vprašanja. Za pravilen odgovor pritisni na gumb.

Razmisli in odgovori pred pritiskom na gumb.

Ali je število $2$ limita funkcije $f(x)$ , ko se $x$ približuje k $1$ ?

Te zanima?

Ali sploh obstaja limita funkcije f(x), ko gre x proti 1? Če obstaja, utemeljite odgovor.

Odgovor

Ali obstaja limita funkcije f(x), ko gre x proti 2? Odgovor utemeljite.

Te zanima?

Odgovor je DA:

$\lim_{x \to 2}f(x)=0$

Utemeljitev: Če bi si naredili tabelo vrednosti funkcije $f(x)$ , ko je $x$ v bližini točke $2$ , bi ugotovili, da bližje kot smo točki $2$ , bolj so vrednosti funkcije blizu $0$ .

Če pa pogledamo na utemeljitev s stališča $\epsilon -$ , $\delta -$ formulacije limite, lahko ugotovimo, da za vsak (poljuben) $\epsilon$ obstaja vedno $\delta$ , ki pa mora zadostiti pogoju: $\delta=|f(2+\delta)–f(2)|<\epsilon$ . To lahko grafično ugotovimo z risanjem različnih $\epsilon$ -okolic števila $0$ na ordinatni osi. Te okolice projeciramo na graf (premico: $y=–x+2$ ), z grafa pa na abscisno os, kjer opredelimo $\delta$ -okolice točke $2$ . Tako kot na gibljivi sliki, s katero smo predstavili limito funkcije.

NE, limita te funkcije, ko gre $x$ proti $1$ , sploh ne obstaja.

Utemeljitev: Recimo, da bi bilo število $b$ iskana limita. Za to limito bi moral za vsak $\epsilon$ obstajati $\delta$ po formulaciji limite.

Če za $b$ vzamemo število manjše od $1$ , potem za $\epsilon <(1–b)$ ne obstaja potreben $\delta$ . Recimo: $b=0,8$ in $\epsilon =0,1$ . Vsaka, še tako majhna, $\delta$ -okolica točke $1$ vsebuje kakšen $x$ iz okolice $(0˙9, 1˙1)$ . Vrednosti funkcije za vsak $x$ iz te okolice pa so večje od $0,9: f(x)>0,9$ . Epsilon okolica za $b=0,8$ in $\epsilon =0,1$ pa je interval $(0˙7, 0˙9)$ , vsebuje vrednosti, manjše od $0,9$ . Tako se za vsak $\delta$ vedno kakšna vrednost iz $\delta$ -okolice preslika zunaj epsilon okolice točke $0,8$ . To pa se pri limiti ne sme zgoditi. Primerne delta okolice ni in število $0,8$ ni limita te funkcije.

Če vzamemo $1≤b≤3$ , potem za $\epsilon <1$ ne obstaja potreben $\delta$ . Recimo: $b=1,5$ in $\epsilon=0,5$ . Vsaka, še tako majhna, $\delta$ -okolica točke $1$ vsebuje kakšen $x$ z intervala $(0, 1)$ . Vrednosti funkcije za vsak $x$ iz tega intervala pa so večje od $2: f(x)>2$ . Epsilon okolica za $b=1,5$ in $\epsilon=0,5$ pa je interval $(1, 2)$ , vsebuje vrednosti, manjše od $2$ . Tako se za vsak $\delta$ vedno kakšna vrednost iz $\delta$ -okolice preslika zunaj epsilon okolice točke $1,5$ . Tako primerne delta okolice ni in število $1,5$ ni limita te funkcije.

Če pa je $b>3$ , potem za $\epsilon<(b–3)$ ne obstaja potreben $\delta$ . Recimo: $b=3,2$ in $\epsilon=0,1$ . Vsaka, še tako majhna, $\delta$ -okolica točke $1$ vsebuje kakšen $x$ iz okolice $(0˙9, 1˙1)$ . Vrednosti funkcije za vsak $x$ iz te okolice pa so manjše od $3: f(x)<3$ . Epsilon okolica za $b=3,2$ in $\epsilon =0,1$ pa je interval $(3˙1, 3˙3)$ , vsebuje vrednosti, večje od $3$ Tako se za vsak $\delta$ vedno kakšna vrednost iz $\delta$ -okolice preslika zunaj epsilon okolice točke $3,2$ . Zopet ni primerne delta okolice in število $3,2$ ni limita te funkcije.

Odgovor je NE, saj za vsako $\epsilon$ -okolico števila $2$ , ko je $\epsilon<1$ , ne obstaja $\delta$ -okolica točke $1$ , ki je potrebna, da bi bilo število $2$ limita funkcije $f(x)$ , ko se $x$ približuje k $1$ . Preprostejša razlaga je: ko se bližamo z $x$ k $1$ z leve, se vrednosti funkcije $f(x)$ približujejo vrednosti $3$ , ko pa se z desne bližamo z $x$ proti $1$ , se vrednosti funkcije $f(x)$ bližajo k $1$ . Tako vrednosti funkcije ne stremijo k istemu številu, ki bi mu rekli limita. Limita funkcije je eno samo število (če sploh obstaja), nikakor pa ne dve števili.

Zaključne besede

Kot vidiš, limita funkcije v dani točki lahko obstaja ali pa tudi ne. Točke, v katerih limita funkcije ne obstaja, so potrebne večje pozornosti. V teh točkah je obnašanje funkcije in njenega grafa nekaj posebnega. V točkah, kjer pa limita funkcije obstaja, pa nam le-ta pove veliko o obnašanju funkcije, o njenih vrednostih, o njenem grafu v ožji okolici te točke.

Dodatne naloge

1. naloga

Realna funkcija je dana s predpisom:

$f(x)=\begin{cases} x^2; & x<-1\\-x; & -1 \leq x \leq 1\\-x^2; & x>1 \end{cases}$

a) Nariši graf funkcije $f(x)$ .

b) Zapiši naslednje limite. Pomagaj si s sliko.

$\lim_{x \to -1}f(x)$

=

$\lim_{x \to 1}f(x)$

=

$\lim_{x \to 2}f(x)$

=

Preveri

Rešitev - graf

Pravilno

Napačno

Poskusi ponovno.

Graf funkcije f(x)

Dodatne naloge

2. naloga

Skiciraj graf realne funkcije

$f(x)=\begin{cases}2^x; & x \leq 0\\log{x}; & 0 \leq x \leq 1\\ (x-1)^3; & x>1 \end{cases}$

in s pomočjo slike določi vrednosti limit, če le-te obstajajo.

$\lim_{x \to 0}f(x)$

$\lim_{x \to 1}f(x)$

$\lim_{x \to 2}f(x)$

Počisti

ne obstaja

$0$

$1$

Preveri

Pravilno

Napačno

Poskusi ponovno.

Dodatne naloge

3. naloga

Ali obstaja limita funkcije

$f(x) =\begin{cases} 2x + 2; & x < −2\\−x − 4; & x \geq -2 \end{cases}$

ko gre $x$ proti $−2$ ? Odgovor utemelji.

Limita ne obstaja

Limita obstaja:

$\lim_{x \to -2}f(x)=2$

Limita obstaja:

$\lim_{x \to -2}f(x)=-2$

Pravilno

Napačno

Poskusi ponovno.

Dodatne naloge

4. naloga

V predpisu realne funkcije

$f(x) =\begin{cases} x - 1;& x < 1\\ −2x + a; & x \geq 1 \end{cases}$

določi parameter $a$ tako, da bo funkcija imela limito v točki $x = 1$ .

Če je parameter $a$ = , ima funkcija $f(x)$ , ko gre $x$ proti $1$ , limito enako .

Preveri

Pravilno

Napačno

Poskusi ponovno, nekje si se zmotil.

Dodatne naloge

5. naloga

Na spodnji sliki je narisan graf funkcije $f(x)$ , ki ima deljen predpis. Kjer se definicijsko območje funkcije deli, so ponavadi tudi težave. Preberi s slike, ali obstajajo naslednje limite:

$\lim_{x \to -2}f(x),$

$\lim_{x \to 1}f(x),$

$\lim_{x \to 2}f(x)$

Če obstajajo, zapiši, kolikšne so.

Slika 1: Funkcija f(x)

Rešitev

$\lim_{x \to -2}f(x)$

ne obstaja, saj lahko z grafa funkcije razberemo:

ko se $x$ bliža $−2$ z leve, gredo funkcijske vrednosti proti $3$ , ko pa se $x$ bliža $−2$ z desne, pa vrednosti funkcije potujejo proti $5$ . Torej ni konkretne vrednosti, ki bi se ji vrednosti funkcije približevale, ko se $x$ konkretno bliža k $−2$ .

Drugi limiti obstajata:

$\lim_{x \to 1}f(x)=2$

$\lim_{x \to 2}f(x)=0$

Limita funkcije

Vaš brskalnik je zastarel

Pritisnite F11

Limita funkcije

Avtor: E-um (vsebinsko), Skupina NAUK (tehnično)

Sodelujoče organizacije

Hvala za ogled gradiva!

Veseli bomo vaših komentarjev. Obiščite nas na www.nauk.si.

Uporabljeni viri

Sodelujoče organizacije

Obstoj limite v točki x=a funkcije f(x) na gibljivi sliki

1. naloga

Pravilno

Napačno

2. naloga

Pravilno

Napačno

3. naloga

Pravilno

Napačno

4. naloga

Pravilno

Napačno

5. naloga

Rešitev

Obstoj limite v točki $x=a$ funkcije $f(x)$ na gibljivi sliki