Polinom p(x) stopnje je realna funkcija, podana s predpisom
pri čemer so , , , ..., , realna števila, ki jim pravimo koeficienti polinoma in , pa je naravno število. Koeficient imenujemo vodilni koeficient, člen vodilni člen, pa prosti, svobodni ali konstantni člen.
|
Stvar izgleda dolga in zapletena. Zakaj smo rekli, da so polinomi ene od najbolj enostavnih funkcij? Če dobro pogledate, kako izgleda polinom, boste videli, da je vsak polinom dobljen s samo končno operacijami seštevanja in množenja. Takšne strukture so nam v algebri zelo všeč. Malo bolj zapletenim izrazom, kjer je poleg seštevanja in množenja uporabljeno še deljenje, pravimo racionalne funkcije.
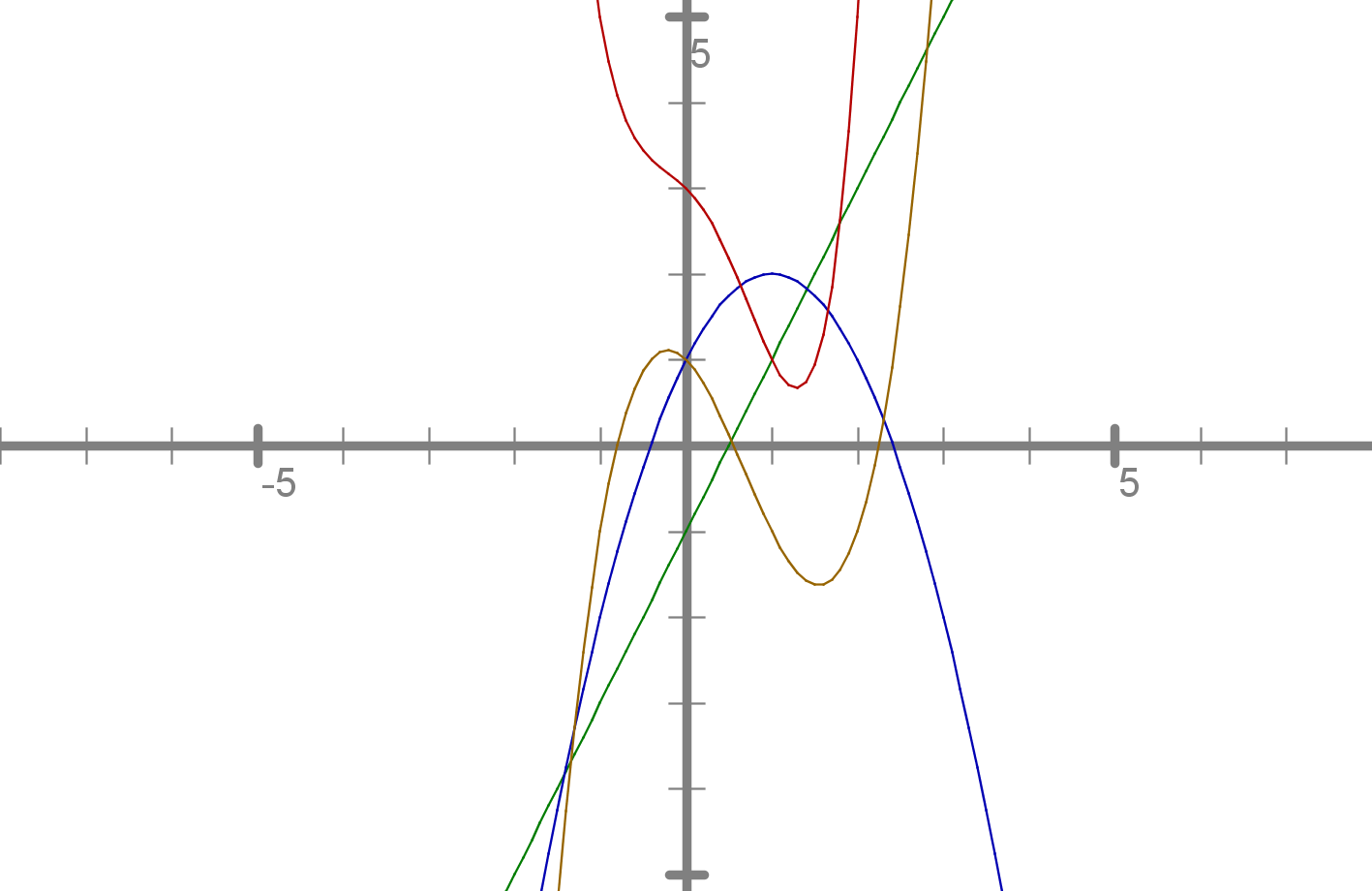
Nekaj primerov grafov polinomov