Pri iskanju ničel kvadratne funkcije smo že reševali preproste kvadratne enačbe, katerih rešitve smo dobili z Vietovim pravilom za razcep tričlenika. Srečali pa smo se tudi že s primeri, ko tričlenika nismo znali razcepiti. Ali to pomeni, da razcep v takšnih primerih ni možen in kvadratna funkcija nima ničel?

Odgovor bomo poiskali kmalu, še prej pa lahko s kratkim testom ponoviš pomen diskriminante, ki nam bo tukaj prišla zelo prav. Če si že prepričan o svojem znanju, pa lahko kviz tudi preskočiš in začneš pri Izzivu.

Premisli in odgovori, ali so naslednje izjave pravilne ali napačne.

Kvadratna funkcija z negativno diskriminanto in negativnim vodilnim koeficientom ima dve različni realni ničli.

Kvadratna funkcija ima eno (dvojno) realno ničlo, če je njena diskriminanta enaka .

Kvadratna funkcija ima realne ničle samo v primeru, če je diskriminanta nenegativna.

Poišči ničle naslednjih kvadratnih funkcij:

1. 
   
   Rešitev lahko preveriš tukaj
   
   
2. 
   
   Pomoč
   
   

Ogledali si bomo postopek, ki nam bo dal formuli za izračun obeh rešitev kvadratne enačbe (ničel kvadratne funkcije). Kadar iščemo ničle kvadratne funkcije, rešujemo torej kvadratno enačbo

Najprej si oglejmo postopek na konkretnem zgledu funkcije iz prejšnjega primera: v ozadju bosta postopek dopolnjevanja do popolnega kvadrata (kot pri izpeljavi temenske oblike enačbe parabole) in pa razcep razlike kvadratov.

Za razliko od postopka pri izpeljavi temenske oblike tokrat zaradi lažjega kasnejšega računanja izpostavimo vodilni koeficient iz vseh treh členov (tukaj je 1, torej ga ni treba) in levo stran dopolnimo do popolnega kvadrata.

Del izraza še skrčimo.

V tej obliki lahko prepoznamo razliko kvadratov, če zapis nekoliko preoblikujemo.

Sedaj je vse pripravljeno za razcep razlike kvadratov.

Produkt bo enak 0, če bo vsaj eden od izrazov enak 0, torej dobimo dve rešitvi. , .

Izpeljimo sedaj še formuli za rešitvi splošne kvadratne enačbe .

Izpostavimo .

Izraz v oklepaju dopolnimo do popolnega kvadrata.

Del izraza damo na skupno ulomkovo črto.

Na tem koraku prepoznamo diskriminanto in zapis lahko nekoliko poenostavimo.

Uporabimo formulo za razliko kvadratov.

Od tod pa dobimo:

Opomba: Rešitvam kvadratne enačbe včasih rečemo tudi "koreni kvadratne enačbe", vendar se bomo mi temu izrazu zaradi možnosti zamenjave s korenom kot aritmetično operacijo izogibali.

Preden se lotimo nalog, si bomo izpeljani formuli za rešitvi kvadratne enačbe ogledali še nekoliko podrobneje.

1. Ali izpeljanima formulama pripada še kakšen pogoj?
   
   Odgovor
   
   
2. Kako vpliva vrednost diskriminante na rešitvi in ?
   
   Razlaga
   
   
3. Kako lahko sedaj zapišemo obliko enačbe kvadratne funkcije z ničlama (faktorizirano obliko)?
   
   Pomoč
   
   

Naloga: Poišči rešitve enačbe .

Rešitev: Izpišimo koeficiente in določimo diskriminanto: , , in . Ker je diskriminanta pozitivna, imamo dve realni rešitvi:

, .

Opomba: Število je eno pomembnejših števil v umetnosti, pa tudi v matematiki – imenujemo ga zlato število. Splača se poiskati več podatkov o njem na svetovnem spletu!

Naloga: Poišči ničle funkcije in nariši njen graf.

Rešitev

Slika parabole

Naloga: Poišči rešitve enačbe

Rešitev

Ne bomo se ustrašili niti kratkega skoka v fiziko.

Naloga: Poišči ničle kvadratne funkcije, ki nam opisuje pot v odvisnosti od časa pri enakomerno pospešenem gibanju:

Rešitev: Zgled je primeren tudi za odvajanje od naših ozkih predstav, da lahko v matematičnih formulah nastopajo samo ene in iste črke. Za iskanje ničel moramo torej rešiti kvadratno enačbo

v kateri je neznanka . Če dobro pogledamo, opazimo, da nam enačbe ni treba reševati po pravkar izpeljanih formulah za ničle, ampak jo lahko rešimo z razstavljanjem (izpostavimo ):

Od tod takoj razberemo rešitvi:

in

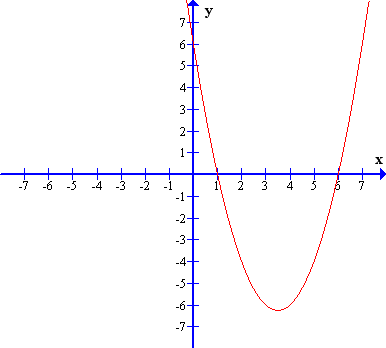
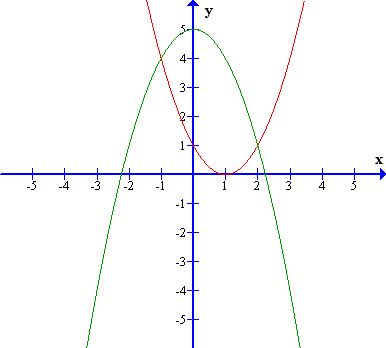
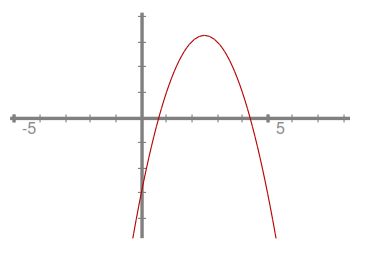
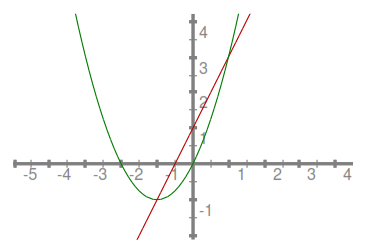
Spodaj sta prikazana primera grafov te kvadratne funkcije, če telo pospešuje oziroma če zavira.

(a) Preveri skladnost med vrednostma presečišč parabole z abscisno osjo (s slike) in vrednostma, ki ju dobimo po formuli za izračun obeh ničel (glede na dana podatka za začetno hitrost in pospešek) v vsakem primeru posebej.

(b) Fizikalno obravnavo rešitev in grafov opravite pri pouku fizike. (Kateri del grafa je smiselno opazovati? Ali znaš pojasniti pomen ničel v vsakem od obeh primerov?)

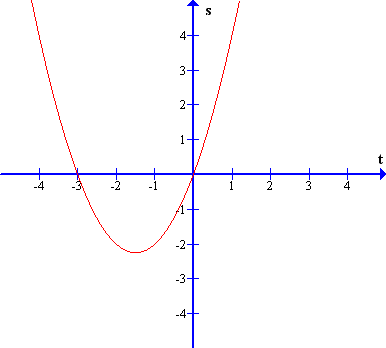
Graf spremembe poti v odvisnosti od časa pri enakomerno pospešenem gibanju, če je začetna hitrost , pospešek pa (pozitiven).

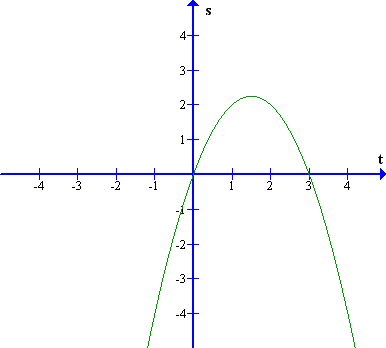
Graf spremembe poti v odvisnosti od časa pri enakomerno pojemajočem gibanju, če je začetna hitrost , pospešek pa (negativen).

Oglejmo si še zgled nekoliko prikrite kvadratne enačbe.

Naloga: Reši enačbo

.

Rešitev

Naloga: Določi presečišča parabol in ter obe paraboli tudi nariši v isti koordinatni sistem.

Rešitev

Slika obeh parabol

Ogledali si bomo reševanje kvadratne enačbe nekoliko drugače – z metodo ploščine: to je eden od pristopov, ki so ga ljudje poznali še pred izpeljavo splošnih formul za iskanje rešitev. S to metodo lahko rešujemo samo kvadratne enačbe določenega tipa, sam pa poskusi na koncu poiskati še kakšno kvadratno enačbo, ki bi se dala tako rešiti.

Naloga: Reši enačbo z metodo ploščine.

Rešitev: Enačbo preoblikujmo tako, da bo njen zapis predstavljal vsoto ploščin dveh pravokotnikov: kvadrata s stranico in pravokotnika s stranicama in . Oglejmo si sliko, ki nam bo to ponazorila.

Sedaj razdelimo pravokotnik s stranico na polovico in dobljeno skrajno polovičko prerazporedimo, kot kaže slika.

Dobljeni sivi lik dopolnimo z rdečim kvadratom do popolnega kvadrata s stranico , kot kaže slika.

Zapišimo sedaj enačbo, ki ponazarja izračun ploščine dobljenega kvadrata s stranico :

.

Na desni strani enačbe nam predstavlja ploščino začetnega sivega lika, pa ploščino dodanega rdečega kvadrata. Skupaj meri ploščina rumenega kvadrata s stranico ravno − glej spodnji prikaz.

Iz dobljene enačbe dobimo s korenjenjem enačbo , od tod pa in ter rešitvi in . Ob tem velja poudariti, da so v času, ko so to metodo prvič uporabili, poznali samo pozitivna števila, zato so takratni reševalci ob reševanju takšne enačbe navedli samo enačbo in rešitev (niso uporabljali zapisa z absolutno vrednostjo).

Vsako izmed nalog najprej reši samostojno ali v paru (papir in svinčnik!), nato poglej v rešitev, ki je pod nalogo.

1. Funkcijo zapiši v temenski obliki, določi njeno teme, ničle in začetno vrednost ter približno nariši njen graf.

Rešitev 1. naloge

2. Obravnavaj vse možne realne rešitve enačbe , kjer je . Ali znaš to enačbo rešiti na tri načine?

Rešitev 2. naloge

3. Reši enačbo .

Rešitev 3. naloge

4. Dana je kvadratna funkcija

.

Izračunaj ničle, teme in začetno vrednost funkcije, zapiši njeno enačbo v temenski in faktorizirani obliki ter nariši njen graf.

Rešitev 4. naloge

5. Dana je kvadratna funkcija , . Koeficient izberi tako, da bo graf funkcije potekal skozi točko . Izračunaj ničli, teme in nariši njen graf.

Rešitev 5. naloge

6. Dani sta premica , , in parabola . Določi tako, da se bo premica dotikala parabole in nato obe približno nariši. Izračunaj tudi absciso dotikališča.

(Namig: Presečišče bo eno samo, če bo diskriminanta enačitvene kvadratne enačbe enaka .)

Rešitev 6. naloge

7. Poišči rešitve kvadratnih enačb in . Ali kaj opaziš? V kakšni zvezi sta obe enačbi?

Rešitev 7. naloge

8. Ugotovitev iz prejšnje naloge dokaži za splošna primera kvadratnih enačb in .

Rešitev 8. naloge

9. Ena od rešitev enačbe je . Določi . Kako imenujemo eno od obeh dobljenih rešitev?

Rešitev 9. naloge

10. V družini funkcij poišči tiste, katerih grafi se dotikajo abscisne osi, in jih nariši.

Rešitev 10. naloge

11.Reši enačbe:

a)

Rešitev

b)

Rešitev

c)

Rešitev

12.Zapiši kvadratne enačbe, ki bodo imele naslednje rešitve:

a) in ,

Rešitev

b) ,

Rešitev

c) in .

Rešitev

13. Nariši graf funkcije , tako da natančno izračunaš ničle, teme in začetno vrednost.

Rešitev

14.Dani sta premica in parabola . Izračunaj morebitna presečišča obeh in ju nariši.

Rešitev