Limite v neskončnosti
Primer za motivacijo
Ni dolgo tega, ko ste v tretjem letniku ugotavljali, kako se grafi polinomov in racionalnih funkcij obnašajo daleč od izhodišča. Obnašanje smo podali zelo opisno, s precej dolgimi stavki, kar pa za matematiko ni značilno. Obnovimo spomin risanja grafa funkcije .
|
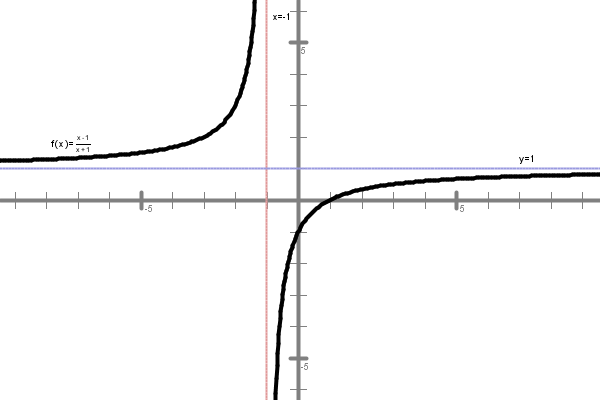
Funkcija je preprosta racionalna funkcija. Pojdimo po korakih, potrebnih za lažje risanje grafa.
1. Ničla funkcije je točka .
2. Pol funkcije je , kar pomeni, da je navpična premica navpična asimptota tega grafa (rdeča premica na spodnji sliki) in da je definicijsko območje množica vseh realnih števil brez ().
3. Glede na ničlo, pol in začetno vrednost lahko določimo predznak funkcije: na intervalih in je funkcija pozitivna, na intervalu pa negativna.
4. Obnašanje funkcije pri velikih vrednostih. Spomnimo se, da ima racionalna funkcija takrat, ko sta stopnji števca in imenovalca enaki, vodoravno asimptoto. (Pri polinomih smo namreč s sklepanjem o spreminjanju vrednosti, ko x raste v neskončnost, ugotovili, da so vrednosti polinoma vse bolj podobne vodilnemu členu. Racionalna funkcija je količnik dveh polinomov, ki ju torej obravnavamo hkrati. Tako lahko sklepamo, da se vrednosti racionalne funkcije daleč od izhodišča bližajo vrednosti količnika vodilnih členov. V našem primeru to pomeni, da se funkcijske vrednosti bližajo kvocientu . Vodoravna asimptota, ki se ji torej bliža graf naše funkcije, je potemtakem premica (modra premica na spodnji sliki).
Pomagamo si lahko še s kakšno točko, ki pripada grafu, in že lahko skiciramo kar dober graf.
Namen
Pojasnilo točke pri postopku risanja prejšnjega grafa je precej dolgovezno in zahteva kar nekaj splošnih, grobih zaključkov. Za natančnega matematika bi lahko bili sporni, premalo natančni. Da bo točka matematično natančna, se moramo pogovoriti o limiti v neskončnosti.
Če v zapisu limite pošljemo v neskončno , namesto k neki točki , imamo opravka z limito v neskončnosti. Torej opazujemo vrednosti funkcije za velike , daleč od izhodišča,
| tako kot točka . Konkretno v našem primeru velja: |
Točka 4
Obnašanje funkcije pri velikih vrednostih. Spomnimo se, da ima racionalna funkcija takrat, ko sta stopnji števca in imenovalca enaki, vodoravno asimptoto. (Pri polinomih smo namreč s sklepanjem o spreminjanju vrednosti, ko x raste v neskončnost, ugotovili, da so vrednosti polinoma vse bolj podobne vodilnemu členu. Racionalna funkcija je količnik dveh polinomov, ki ju torej obravnavamo hkrati. Tako lahko sklepamo, da se vrednosti racionalne funkcije daleč od izhodišča bližajo vrednosti količnika vodilnih členov. V našem primeru to pomeni, da se funkcijske vrednosti bližajo kvocientu . Vodoravna asimptota, ki se ji torej bliža graf naše funkcije, je potemtakem premica (modra premica na spodnji sliki).
Definicija
Spoznajmo limito v neskončnosti. Dogovorimo se:
če za vsako pozitivno število obstaja tako realno število , da velja: če je , potem je .
Drugače zapisan pogoj za obstoj limite: če je , potem je v -okolici točke .
Dinamična slika
Komentar spodnje slike
Na dinamični sliki lahko s premikanjem točke na drsniku za epsilon spreminjaš velikost -okolice točke . Lahko pa tudi sprožiš animacijo spreminjanja ε-okolice, tako da najprej izbereš ikono za animacijo, potem pa trikrat zapored klikneš na točko na drsniku.
Ko se torej igraš z velikostjo -okolice točke , se spreminja položaj točke , ki označuje mejo, od katere naprej točke grafa ležijo v pasu -okolice točke .
Dinamična slika
Kaj ugotoviš?
Spreminjaj velikost -okolice točke – spreminjaj širino pasu, obarvanega modro. Kako se spreminja položaj točke oziroma velikost števila ? Preden pritisneš na Odgovor, postavi svojo trditev, hipotezo.
Opaziš lahko, da za manjši dobiš večji . Vendar pa za vsak, še tako majhen , obstaja ustrezen . Kar pomeni, da je točka limita funkcije , ko gre v neskončno, saj so vse točke grafa, ki imajo , v modrem pasu, kar pomeni, da so v -okolici točke .
Primer
Primera elementarnih funkcij, ki imata limito v neskončnosti
Taki funkciji sta potenčna in eksponentna , kjer je osnova na intervalu – med in .
Oglejmo si najprej funkcijo . Preučimo znova njen graf, ko vrednosti rastejo čez vse meje.
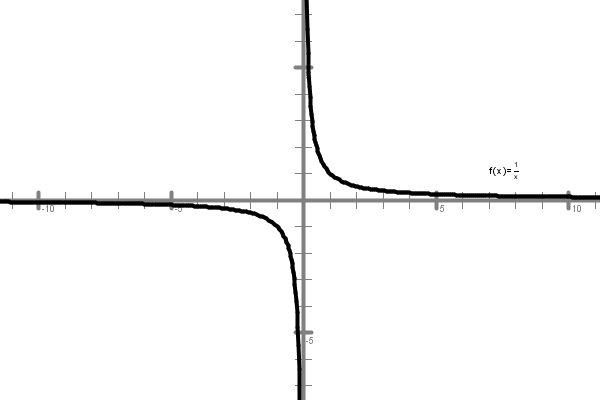
Graf potenčne funkcije
O grafu in limiti te funkcije v neskončnosti
Če opazuješ graf, ko raste v neskončnost, ko gremo po osi vse bolj desno, se krivulja grafa vse bolj bliža abscisni osi. Kar pomeni, da so vrednosti funkcije vse bolj podobne . In lahko sklepamo, da je:
Da bilo bi to dejstvo resnično, mora za vsak obstajati . Poiščimo tak .
Za vsak mora veljati: .
, ker gre v neskončnost, je pozitiven in je . Zato lahko zapišemo:
oziroma: .
Tako lahko za vzamemo obratno vrednost števila : .
Za vsako še tako majhno število obstaja , tako da so za točke desno od vrednosti v epsilon okolici števila .
| Kar torej pomeni |
Primer
Oglejmo si zdaj eksponentno funkcijo . Če je , je eksponentna funkcija naraščajoča čez vse meje, ko vrednost večamo v neskončnost. Zato je brez smisla iskati število , ki bi bilo limita v neskončnosti za eksponentno funkcijo z osnovo, večjo od . Če pa je , imamo položaj, podoben položaju v prejšnjem primeru.
Poglejmo konkretno funkcijo . Spet preuči njen graf, ki je na spodnji sliki. Posveti se vrednostim funkcije za velike .
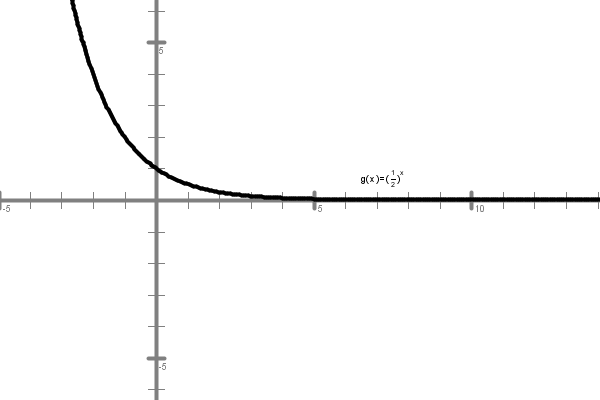
Graf eksponentne funkcije
O grafu in limiti te funkcije v neskončnosti
Če opazuješ graf, ko raste v neskončnost, ko gremo po osi vse bolj desno, se krivulja grafa vse bolj bliža abscisni osi. Kar pomeni, da so vrednosti funkcije vse bolj podobne , skoraj bi lahko rekli, da so vrednosti enake . Pa če malo pomisliš na izraz in zalogo vrednosti katere koli eksponentne funkcije, veš, da vrednosti te funkcije nikoli niso enake . So pa za velike zelo blizu in lahko sklepamo, da je: če je .
če je |
Upoštevajmo definicijo limite v neskončnosti in preverimo, ali res za vsak lahko dobimo , da bo veljalo: za vsak mora . Poiščimo tak .
, saj so vrednosti eksponentne funkcije vedno pozitivne. Zato lahko zapišemo:
oziroma: . Če obe strani neenakosti logaritmiramo z naravnim logaritmom, sledi: . To smemo narediti, saj je funkcija naravni logaritem, injektivna in naraščajoča. Nadaljujemo lahko tako, da obe strani neenakosti delimo z , pri tem pa se moramo zavedati, da je to število negativno in moramo znak neenakosti obrniti. lna je negativno, ker je osnova med in , naravni logaritem pa je za te vrednosti spremenljivke negativen. Tako dobimo neenakost: .
Tako lahko za vzamemo prav ta količnik: .
Za vsako še tako majhno število obstaja , da velja: če je , potem je . Kar pomeni, da je res limita funkcije , ko gre v neskončnost in je osnova med in .
Limita v neskončnosti in risanje grafa
Kako si torej pomagamo z limito v neskončnosti pri risanju grafa?
Če je limita v neskončnosti funkcije enaka številu , se to na grafu prepozna kot vodoravna asimptota, ki se ji krivulja približuje vse bolj, ko raste čez vse meje, torej v neskončnost. Ta vodoravna asimptota ima enačbo , je premica, ki seka ordinatno os v točki in je vzporedna -osi. Točko pri risanju grafa v prvem primeru lahko sedaj zamenjamo s konkretno matematično interpretacijo obnašanja v neskončnosti in zapišemo takole:
| 4. | zato je premica vodoravna asimptota grafa, ko gre . |
Točka 4
Obnašanje funkcije pri velikih vrednostih. Spomnimo se, da ima racionalna funkcija takrat, ko sta stopnji števca in imenovalca enaki, vodoravno asimptoto. (Pri polinomih smo namreč s sklepanjem o spreminjanju vrednosti, ko x raste v neskončnost, ugotovili, da so vrednosti polinoma vse bolj podobne vodilnemu členu. Racionalna funkcija je količnik dveh polinomov, ki ju torej obravnavamo hkrati. Tako lahko sklepamo, da se vrednosti racionalne funkcije daleč od izhodišča bližajo vrednosti količnika vodilnih členov. V našem primeru to pomeni, da se funkcijske vrednosti bližajo kvocientu . Vodoravna asimptota, ki se ji torej bliža graf naše funkcije, je potemtakem premica (modra premica na spodnji sliki).
Pravila za računanje in primeri
Pri računanju limite v neskončnosti veljajo ista pravila kot pri običajni limiti funkcije. Ta pravila smo že predelali in jih znamo uporabljati. Za osvežitev spomina: limita vsote je vsota limit, limita razlike je razlika limit, limita produkta je produkt limit in limita količnika je količnik limit, če ni limita imenovalca enaka . Ta pravila lahko preprosto izpelješ, če zgolj upoštevaš definicijo limite.
Primer 1
Za prvi primer uporabe pravil za računanje limit v neskončnosti vzamemo funkcijo .
Za izračun potrebujemo samo pravilo produkta. Tako ugotovimo, da je limita v neskončnosti potenčne funkcije z negativnim celim eksponentom enaka . Na grafu te funkcije na spodnji sliki se to prepozna tako, da se krivulja grafa asimptotsko približuje abscisni osi. Po zgoraj zapisanem sklepu je namreč premica vodoravna asimptota grafa, to pa je ravno os .
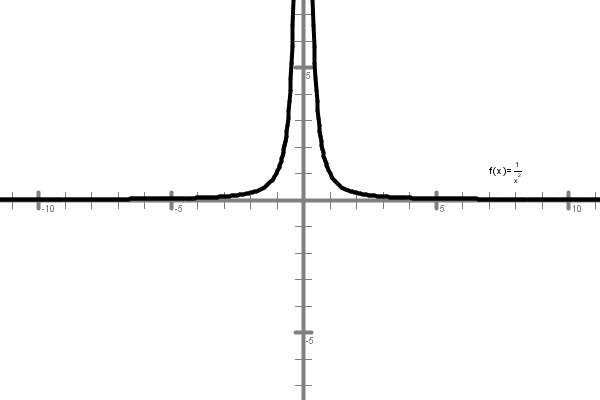
Graf funkcije
Pravila za računanje in primeri
Primer 2
Za računanje limite v neskončnosti racionalne funkcije uporabimo malo spretnega računanja, da zadevo prevedemo v bolj domače okolje. Pa začnimo.
Najprej torej razširimo ulomek z . Tako smo dobili v števcu in imenovalcu funkcije, ki imajo limite v neskončnosti in jih poznamo. Nato preprosto uporabimo pravilo količnika, vsote in razlike. Limita funkcije v neskončnosti je torej enaka , kar pomeni, da je premica vodoravna asimptota grafa te funkcije – modra premica na spodnji sliki.
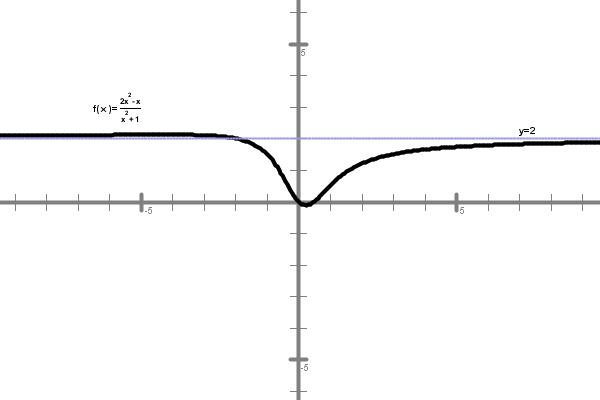
Graf racionalne funkcije
Limita v minus neskončnosti
Podobno bi lahko definirali limito v minus neskončno. Da bi se temu izognili, se dogovorimo takole:
Torej, če poznaš limito v neskončnosti za funkcijo , poznaš tudi limito v minus neskončnosti funkcije . S tem pa lahko opredelimo obnašanje funkcije daleč od izhodišča tudi v levo stran koordinatnega sistema.
Če se spomnimo na lihe in sode funkcije, lahko zapišemo naslednjo ugotovitev:
| Za sode funkcije velja: | |
| Za lihe funkcije pa velja: |
Limita v minus neskončnosti
Primer
Preizkusimo funkcijo , ki ni ne soda ne liha.
Najprej izračunajmo limito v neskončnosti:
Torej ima graf te funkcije v plus neskončno vodoravno asimptoto . Sedaj pa izračunajmo še limito v minus neskončno:
Torej ima graf te funkcije tudi v minus neskončno vodoravno asimptoto . To lahko vidimo na spodnji sliki grafa funkcije , kjer je vodoravna asimptota narisana z rdečo barvo.
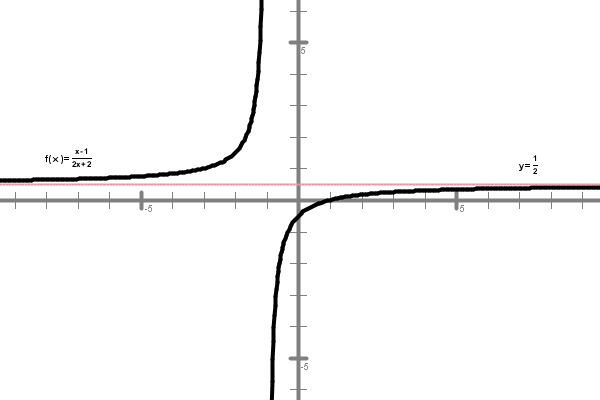
Graf funkcije
Dodatne naloge 1
Vaja dela mojstra
Če želiš obvladati limito v neskončnosti in jo uporabljati pri utemeljevanju risanja grafov funkcij, moraš narediti čim več nalog. Zato priporočam, da narediš naslednje naloge.
Izračunaj!
| a) |
Pravilno
Pojdi na naslednjo nalogo.
Razširi ulomek z .
Rešitev
Dodatne naloge 1
Pravilno
Pojdi na naslednjo nalogo.
Razširi ulomek z .
Rešitev
Dodatne naloge 1
Pravilno
Pojdi na naslednjo nalogo.
Razširi ulomek z .
Rešitev
Dodatne naloge 1
Pravilno
Pojdi na naslednjo nalogo.
Razširi ulomek z .
Rešitev
Dodatne naloge 1
Pravilno
Pojdi na naslednjo nalogo.
Razširi ulomek z .
Rešitev
Dodatne naloge 1
Pravilno
Pojdi na naslednjo nalogo.
Razširi ulomek z .
Rešitev
Dodatne naloge 2
Pravilno
Pojdi na naslednjo nalogo.
Razširi ulomek z .
Rešitev
Dodatne naloge 2
Poveži!
Pravilno
Pojdi na naslednjo nalogo.
Napačno
Še enkrat poskusi.
Rešitev
Dodatne naloge 3
Pravilno
Pojdi na naslednjo nalogo.
Razširi ulomek z .
Rešitev
Dodatne naloge 3
Pravilno
Pojdi na naslednjo nalogo.
Najprej uporabi pravilo vsote za računanje limite, nato v prvem členu razširi ulomek z .
Rešitev
Dodatne naloge 2
Poveži!
Pravilno
Pojdi na naslednjo nalogo.
Napačno
Še enkrat poskusi.
Rešitev
Dodatne naloge 4
Pravilno
Napačno
Še enkrat poskusi.
Limiti v neskončnosti in v minus neskončnosti sta enaki :
| in |
|
|