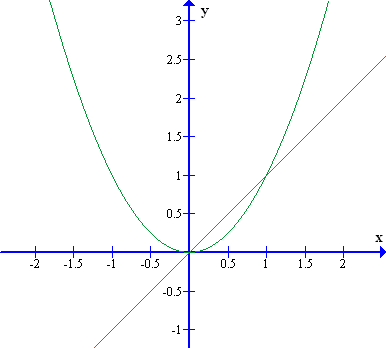Uvodoma bomo ponovili nekaj osnovnih pojmov, ki jih obravnavamo pri realnih funkcijah, in jih v zgledih opazovali pri kvadratni funkciji. Prav tako bomo na začetku obravnavali lastnosti kvadratne funkcije z risanjem njenega grafa s pomočjo računalnika, nato pa bomo spoznali postopek, s katerim bomo lahko graf poljubne kvadratne funkcije narisali tudi sami.

Prvi nam že dobro znani pojem

Samostojno ali v paru reši naslednje naloge.

• Določi ničle kvadratne funkcije .
  
  Resitev je skrita tukaj
  
  

• Ali lahko na podlagi zgornjega primera sklepamo, da ima kvadratna funkcija vedno dve realni ničli? Poišči vsaj dva protiprimera, če seveda obstajata.
  
  Potrebuješ pomoč?
  
  

  Še izziv za naprej

  Ali je tudi v teh splošnejših primerih kvadratnih funkcij njihov graf parabola?
  
  Razlago poišči tukaj
  
  

Tudi naslednji pojem nam je že dobro znan:

Določi začetne vrednosti funkcij , in .

Odgovor

Z žepnim računalom poišči kvadrate naslednjih števil: in . Vsak kvadrat po velikosti primerjaj s številom, ki si ga kvadriral. Kaj opaziš? Ali se števila s kvadriranjem zvečajo ali zmanjšajo?

Ugotovitev se nahaja tukaj

Zgornjo ugotovitev lahko lepo ponazorimo tudi s primerjavo grafov linearne funkcije in kvadratne funkcije : na intervalu leži parabola pod premico , na intervalu pa nad njo.

V predhodnem gradivu smo pokazali, da je graf osnovne kvadratne funkcije parabola. Zanima nas, ali je tudi graf poljubne kvadratne funkcije parabola.

Pred nadaljevanjem najprej ponovi lastnosti parabole in lastnosti vzporednega premika grafa funkcije − oboje smo spoznali že v prejšnjih gradivih.

Oglejmo si, kaj dobimo pri vzporednem premiku parabole : pri vzporednem premiku za vektor se parabola premakne v graf . Ta graf ima še vedno obliko parabole, saj se vsaka točka na paraboli premakne za dani vektor. Za ponazoritev te ugotovitve si pomagaj s konstrukcijo.

Premikaj drsnika in opazuj, ali se oblika parabole pri tem spremeni. Ali lahko dobimo še kaj drugega razen parabole? Oznaka predstavlja prvo komponento, oznaka pa drugo komponento vektorja vzporednega premika.

Sedaj moramo še pokazati, da lahko graf poljubne kvadratne funkcije dobimo z ustreznim vzporednim premikom parabole .

Če odpravimo oklepaj v predpisu , dobimo:

Od tod vidimo, da smo z vzporednim premikom res dobili graf neke splošnejše kvadratne funkcije s kvadratnim, linearnim in svobodnim členom, pri čemer so koeficienti in .

Iz pravkar dobljenega sistema enačb lahko ugotovimo, s katerim vektorjem vzporednega premika dobimo iz osnovne parabole graf izbrane kvadratne funkcije : iz druge enačbe dobimo takoj

iz tretje enačbe , ob upoštevanju pravkar izpeljanega izraza za pa:

S tem smo dokazali, da je tudi graf poljubne kvadratne funkcije parabola.

Ob nalogah si bomo ogledali še dve lastnosti kvadratne funkcije.

• Kdaj rečemo, da je funkcija soda? Kako v koordinatnem sistemu prepoznamo graf sode funkcije? Ali je kvadratna funkcija soda? Kaj pa funkcija ? Izpelji pogoj za sodost funkcije .
  
  Odgovori so skriti tukaj
  
  

• Simetrijska os parabole je premica, glede na katero je parabola simetrična. Ta pojem nam je sicer že znan iz osnovne šole, ko smo govorili o simetrijski osi lika. Ali najdeš kakšno simetrijsko os parabole ? Kaj pa simetrijsko os parabole ?
  
  Pomoč
  
  

V uvodni uri o kvadratni funkciji smo spoznali, da je teme najnižja ali pa najvišja točka parabole.

V nadaljevanju si bomo ogledali dva pristopa k računanju koordinat temena, še enega (morda najelegantnejšega) pa si bomo prihranili za 4. letnik. Najprej pa si oglejmo zgled določanja koordinat temena samo z dosedanjim znanjem o vzporednem premiku parabole .

Določi koordinati temena parabole

Preveri svoj odgovor

V primeru parabole pa bomo na pamet le stežka ugotovili, za kakšen vektor smo premaknili osnovni graf , saj v zapisu nastopa še linearni člen. Spoznali smo sicer že formuli za izračun komponent in vektorja vzporednega premika, od koder lahko takoj dobimo tudi koordinati temena , a bomo tokrat spoznali še drugačen način, s katerim bomo enačbo poljubne parabole preoblikovali v temensko obliko – metoda se imenuje dopolnjevanje do popolnega kvadrata. Najprej si jo bomo ogledali na enostavnejšem konkretnem zgledu, nato pa še pri splošnih koeficientih.

S preoblikovanjem splošne oblike parabole v temensko obliko

Enačbo preoblikujmo v temensko obliko.

Izpostavimo vodilni koeficient iz kvadratnega in linearnega člena.

Izraz v oklepaju dopolnimo do popolnega kvadrata (koeficient linearnega člena razpolovimo in od oklepaja odštejemo kvadrat te razpolovljene vrednosti, pomnožen z vodilnim koeficientom):

.

Izraz polepšamo.

.

Odčitamo koordinati temena; teme je točka:

.

Na tem koraku bomo zaradi večje preglednosti zapisov vpeljali novo količino

S pomočjo diskriminante sedaj zapišimo:

Iz temenske oblike enačbe parabole lahko sedaj odčitamo še koordinati temena in simetrijsko os parabole.

Ker je parabola simetrična glede na simetrijsko os skozi teme parabole in sta ničli prav tako simetrični glede na to os (glej utemeljitev), lahko absciso temena izračunamo kot aritmetično sredino ničel in :

Ordinato nato izračunamo kot .

Utemeljitev

Zgled

Določi teme parabole

Rešitev

Curek vode ima obliko parabole.

V prejšnjem poglavju smo pokazali, da je graf poljubne kvadratne funkcije parabola. Parabola je tir mnogih gibanj v naravi; enega takšnih nam prikazuje tudi zgornji filmček.

Zanimivost: Prav tako se po parabolah giblje kamen pri igri "skakanje žabice" po vodni gladini. To igro so nekateri spremenili celo v tekmovalni "šport" in na svetovnem spletu lahko poiščeš podatek in posnetek za trenutni svetovni rekord v številu odbojev kamna na vodni gladini (ang. stone skipping).

Opremljeni smo z dovolj veliko malho znanja, da se lahko lotimo risanja grafa kvadratne funkcije, katere enačba se da enostavno razcepiti po pravilu za razcep tričlenikov (Vietovo pravilo).

Dana je funkcija

.

Narišimo njen graf z obravnavo njenih lastnosti.

Nalogo bomo reševali po korakih (takšnemu načinu rečemo tudi analitični pristop).

1. Ničle:

2. Začetna vrednost:

,

kar takoj razberemo iz enačbe (svobodni člen), torej je

.

3. Teme: s preoblikovanjem v temensko obliko

Teme je .

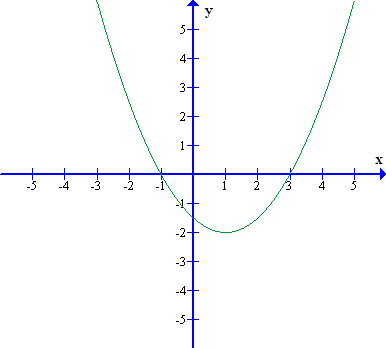
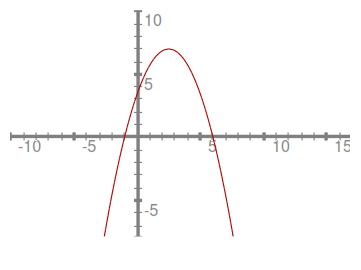
4. Sedaj smo pripravljeni za risanje njenega grafa. Po označitvi koordinatnih osi, enot in izhodišča narišemo najprej točki, kjer sta ničli. Sledi označitev začetne vrednosti in temena. Ker poznamo os simetrije, ki poteka skozi teme, lahko narišemo zrcalno sliko začetne vrednosti in tako pridobimo še eno točko parabole. Končno smo pripravljeni na risanje krivulje: ker je vodilni koeficient med in , je parabola v okolici temena bolj zaobljena oz. narašča manj strmo.

Opomba: V primerih, ko nam tipične točke (ničle, ...) ne bi dale dovolj informacij o obliki parabole, si lahko pomagamo tudi s tabelo in izračunom koordinat nekaterih dodatnih točk. (Bolj zagnani dijaki pa se lahko takšnih problemov lotite tudi z ustreznimi transformacijami preprostejših grafov.)

Končno dobimo graf funkcije

,

ki mora biti takšen:

S pomočjo izračunanih vrednosti in slike lahko obravnavamo še nekaj lastnosti:

(a) definicijsko območje so vsa realna števila (kot pri vseh kvadratnih funkcijah):

,

(b) zaloga vrednosti so vsa realna števila, ki so večja ali enaka (ker je teme najnižja točka parabole):

,

(c) simetrijska os je premica ,

(č) funkcija ni niti soda niti liha (preveri z računom!),

(d) funkcija je padajoča za

in naraščajoča za

,

(e) funkcija ni injektivna in zato tudi ne bijektivna; je pa bijektivna npr. za

.

V zvezek nariši grafe naslednjih funkcij, tako da obravnavaš njihove lastnosti kot v prejšnjem zgledu.

1. Kako bi narisal graf funkcije s pomočjo vzporednega premika ustreznega grafa?
   
   Rešitev
   
   

2. Dana je kvadratna funkcija

   1. Določi začetno vrednost funkcije in izračunaj njeni realni ničli, če obstajata.
      
      Rešitev
      
      
   2. Funkcijski predpis za funkcijo zapiši v temenski obliki (z dopolnjevanjem do popolnega kvadrata) in določi koordinati temena.
      
      Rešitev
      
      
   3. Nariši graf funkcije .
      
      Rešitev
      
      

1. Iz družine parabol določi tiste, ki dosežejo ekstremno vrednost pri .
   
   Rešitev
   
   
2. Določi simetrijsko os parabole .
   
   Rešitev
   
   
3. Pri katerem pogoju je kvadratna funkcija soda?
   
   Rešitev
   
   
4. Vsota celih števil in je enaka . Določi ti dve števili, tako da bo njun produkt največji možen. Kaj pa v primeru, ko je njuna vsota enaka ?
   
   Rešitev