Za hip se posvetimo funkciji . Se spomniš, čemu je enak odvod te funkcije?
(x)
Ali znaš zapisati tudi odvod funkcije ?
(x)
Nedoločeni integral
Nedoločeni integral
E-um (vsebinsko), Skupina NAUK (tehnično)
Spomnimo se
Rešitev
Tvoj rezultat je /2.
Izziv
Z mislijo na pravkar rešen primer odgovori na naslednja vprašanja.
1. Katero funkcijo moramo odvajati, da dobimo funkcijo ? Izberi med spodnjimi odgovori izberi pravilnega.
2. Ali je to edini možni odgovor? Pojasni svoje razmišljanje.
3. Vse funkcije, ki imajo enak odvod (kot funkcijo), se razlikujejo med seboj v vrednosti prištete ali odštete konstante vrednosti eksponenta spremenljivke vrednosti koeficienta spremenljivke . Na koncu lahko imamo v njihovem zapisu katero koli konstanto funkcijo spremenljivko .
Odgovor
Pri tovrstnem problemu je več možnih odgovorov: na primer, tudi odvodi funkcij , in so med seboj enaki.
Primerov takšnih funkcij je torej neskončno mnogo, saj je odvod prištetega ali odštetega realnega števila vedno enak .
Pravilno
Narobe
Rešitev
1. F(x)=x^2
2. Pri tovrstnem problemu je več možnih odgovorov: na primer, tudi odvodi funkcij , in so med seboj enaki.
Primerov takšnih funkcij je torej neskončno mnogo, saj je odvod prištetega ali odštetega realnega števila vedno enak .
3. Vse funkcije, ki imajo enak odvod (kot funkcijo), se razlikujejo med seboj v vrednosti prištete ali odštete konstante. Na koncu lahko imamo v njihovem zapisu katero koli konstanto.
Izziv
Povzetek
V vsakem od zgornjih primerov si izračunal nedoločeni integral funkcije : vsaki od funkcij, kjer je poljubna konstanta in velja
bomo namreč rekli nedoločeni integral funkcije .
Zapišimo ta naš dogovor splošneje, skupaj z majhnim dodatkom.
Nedoločeni integral funkcije na intervalu je taka funkcija , katere odvod je enak funkciji na tem intervalu. To zapišemo s simboli takole:
Poimenovanja:
- – integralski znak (izhaja iz črke S in besede die Summe - vsota; razlog za njegovo uporabo bomo spoznali pri določenem integralu);
- – integrand;
- – diferencial neodvisne spremenljivke (razlog za njegovo uporabo bomo spoznali pri določenem integralu);
- – integracijska spremenljivka;
- – oznaka za nedoločeni integral funkcije .
1. Zgled
Naloga
Poišči nedoločeni integral kvadratne funkcije .
Rešitev
Navodilo oziroma cilj naloge lahko zapišemo v obliki
No, pa poskusimo: po krajšem premisleku ugotovimo, da lahko zapišemo:
Ker pa smo pri . vprašanju uvodnega izziva že ugotovili, da se vsi nedoločeni integrali dane funkcije razlikujejo med seboj za konstanto, bomo to nakazali z zapisom:
Z dodano konstanto bomo nakazali, da ima vsaka izbrana funkcija več nedoločenih integralov, ki se med seboj razlikujejo v prišteti konstanti , saj je odvod konstante enak in na odvod torej ne vpliva. Pri računanju nedoločenih integralov torej ne pozabi dopisati konstante .
Preveri svoje razumevanje nedoločenega integrala
Rešitev
- k je konstanta:
o5
Tvoj rezultat je /3.
Še en kratek izziv
Naslednji problem nam bo prikazal razliko med zahtevnostjo odvajanja (iskanja odvoda dane funkcije) in zahtevnostjo integriranja (iskanja nedoločenega integrala dane funkcije).
1. Ali znaš izračunati odvod funkcije ?
Izmed ponujenih odgovorov izberi njegov funkcijski predpis?
2. Ali znaš izračunati tudi nedoločeni integral funkcije f? |
Pravilno
Narobe
Pomoč
Verjetno ti kljub mnogim poskusom to ni uspelo. Opazimo torej, da je postopek iskanja odvoda poljubne funkcije veliko lažji kot postopek iskanja nedoločenega integrala poljubne funkcije. Pri odvajanju uporabljamo znana pravila za odvod vsote, produkta, kvocienta in kompozituma funkcij, pri iskanju nedoločenega integrala pa takšnih preprostih formul ni. Pod naslednjim gumbom si oglej sliko grafa te zanimive funkcije , nato pa sledi še zapis enega dogovora.
Slika funkcije
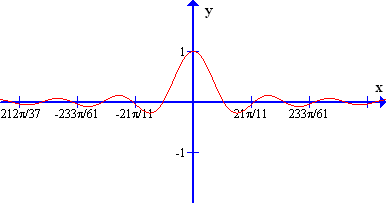
Opomba: v točki je funkcija nedoločena , vendar funkcijska vrednost tam limitira k , saj je
2. Zgled
Funkciji in sta primera integrabilnih funkcij: nedoločeni integral funkcije znamo poiskati in je preprost, nedoločenega integrala funkcije pa ne znamo (niti ne moremo) izraziti z elementarnimi funkcijami (ta primer navajamo zgolj kot zanimivost, saj je utemeljitev tega za nas prezahtevna).
Za radovedne
Zakaj v definiciji potrebujemo še dodatni pogoj z intervalom ?
Spomnimo se, da je
Vprašajmo se, ali lahko od tod kar takoj zapišemo zvezo
Za radovedne
Zakaj v definiciji potrebujemo še dodatni pogoj z intervalom ?
Da, vendar z določenimi omejitvami: funkcija je namreč definirana na intervalu , medtem ko je funkcija definirana le na intervalu . Prva enakost velja le na intervalu , zato tam velja tudi druga enakost. Če pa si pogledamo drugo enakost, vidimo, da je integrand definiran tudi na intervalu . Zato nas zanima, katera funkcija je nedoločeni integral na tem intervalu: že ne, saj na ni definiran. Ali bi lahko zapis nekoliko popravili tako, da bo definiran tudi na , hkrati pa se z njim na ne bo nič spremenilo? Če se spomnimo, katera matematična funkcija nam negativna števila „spremeni v pozitivna števila, pozitivna pa pusti pri miru”, dobimo odgovor: to je absolutna vrednost. Zapis se mora torej glasiti . Sedaj res na celem definicijskem območju funkcije velja:
To si lahko pogledaš tudi na sliki grafov pod spodnjim gumbom.
V splošnem je torej pomembno vedeti, na katerem intervalu je neka funkcija nedoločeni integral druge funkcije, a ker želimo v srednji šoli pridobiti le pregledno znanje o nedoločenem integralu, se s takšnimi vprašanji ne bomo podrobneje ukvarjali.
Slika grafov obeh funkcij
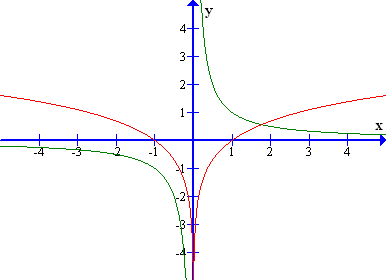
Grafa funkcij (zelen) in (rdeč) se ujemata v definicijskem območju.
Pojem primitivne funkcije
Včasih pri nedoločenem integralu omenjamo še pojem primitivne funkcije. Primitivna funkcija funkcije je taka funkcija, katere odvod je enak funkciji na intervalu .
Primitivne funkcije niso enolično določene; za sta primitivni funkciji na primer in ; seveda jih je neskončno mnogo. Primitivna funkcija je torej sopomenka za nedoločeni integral.
Dve lastnosti
Za sklep tega uvodnega seznanjanja z nedoločenim integralom si poglejmo še dve lastnosti.
Dokaz te lastnosti je za nas prezahteven, veliko bolj samoumeven pa nam je obrat te trditve: če imamo konstantno funkcijo na nekem intervalu , je tam njen odvod enak .
Naslednjo lastnost smo spoznali že pri uvodnem izzivu, za radovednejše pa jo bomo sedaj tudi dokazali.
Dokaz za radovedne
Naj bosta in nedoločena integrala funkcije na nekem odprtem intervalu , torej je in na .
Poglejmo si odvod njune razlike:
Ker sta in tudi zvezni tam, kjer sta definirani, je po prvi lastnosti njuna razlika konstantna na :
, kjer je konstanta.
Od tod sledi sklep, da se razlikujeta za aditivno konstanto.
Ponovitev
Tabela odvodov nekaterih elementarnih funkcij
Pred nadaljevanjem si osvežimo spomin na tabelo odvodov elementarnih funkcij.
Razišči
1. K integralu v levem stolpcu, dodaj ustrezno funkcijo iz desnega stolpca, da bo enakost veljala.
Rešitev
Napačno
Nekje si naredil napako.
Poskusi ponovno.
Pravilno
Razišči
2. K integralu v levem stolpcu, dodaj ustrezno funkcijo iz desnega stolpca, da bo enakost veljala.
Rešitev
Napačno
Nekje si naredil napako.
Poskusi ponovno.
Pravilno
Razišči
3. Ali vedno velja ?
Pravilno
Formula velja za vsako realno število razen za število , ker je ulomek tam nedefiniran. Za velja:
Napačno
Formula velja za vsako realno število razen za število , ker je ulomek tam nedefiniran. Za velja:
Dopolni
S pomočjo tabele odvodov elementarnih funkcij dopolni spodnjo tabelo nedoločenih integralov elementarnih funkcij. Svoje rešitve preveri z odvajanjem.
Dopolni manjkajoče podatke v tabeli. (Rešitve vnašaj brez presledkov.)
| + | /( ) + |
| / + | |
| (x) + | |
| + | + |
Rešitev
Rezultat
Tvoj rezultat je /17
3. Zgled
Naloga
Poišči predpis funkcije , katere odvod je enak , njen graf pa poteka skozi koordinatno izhodišče.
Rešitev
Vemo, da je . Funkcija je torej nedoločeni integral funkcije , o funkciji pa še dodatno vemo, da ima v vrednost . S pomočjo tabele lahko izračunamo:
Ker leži točka na grafu funkcije , je in lahko pišemo:
in že imamo predpis funkcije f:
Na koncu zapišimo tabelo nedoločenih integralov elementarnih funkcij še v celoti.
Tabela
Tabela nedoločenih integralov nekaterih elementarnih funkcij
Utrjevanje
Vzemi si nekaj časa in se nauči tabelo nedoločenih integralov osnovnih funkcij, nato pa svoje znanje preizkusi še pri spodnjih nalogah. Vsako od nalog najprej reši s svinčnikom in papirjem, nato pa pod gumbi preveri svoje rešitve.
Rezultat
Tvoj rezultat je /7
Rešitve
Zapis s korenom preoblikujemo v zapis s potenco z racionalnim eksponentom, uporabimo ustrezno pravilo, na koncu pa rezultat zapišemo v takšni obliki, kot je podana začetna funkcija (integrand): če smo imeli v začetku zapis s koreni, naj bo takšne oblike tudi rešitev, če pa imamo zapis v obliki potence, zapišemo tudi rešitev v obliki potence.
Integracijska spremenljivka je lahko seveda tudi kaj drugega kot le običajni x.
Rezultate na koncu poenostavimo: odpravimo dvojne ulomke, racionaliziramo imenovalce, okrajšamo ulomke in delno korenimo izraze.
Preden se lotimo reševanja s poskušanjem, izraze preoblikujemo do bolj znanih oblik z uporabo znanih zvez med kotnimi funkcijami.
Dodatne naloge
1. Naloga
Odgovori.
a) Katero funkcijo moramo integrirati, da dobimo funkcijo ?
Rešitev
Iščemo odvod funkcije , torej je odgovor .
Narobe
Poskusi ponovno.
Pravilno
Dodatne naloge
1. Naloga
Odgovori.
b) Katero funkcijo moramo odvajati, da dobimo funkcijo , če graf funkcije vsebuje točko ?
Rešitev
Najprej poiščemo nedoločeni integral funkcije , ki je v našem primeru , ob upoštevanju točke pa dobimo .
Narobe
Poskusi ponovno.
Pravilno
Dodatne naloge
2. Naloga
Nariši nekaj primerov grafov nedoločenih integralov funkcije . Primeri grafov
V čem se med seboj razlikujejo vsi nedoločeni integrali? Po aditivni konstanti . Po eksponentu spremenljivke Vsi nedoločeni integrali so enaki.
S katero transformacijo ravnine lahko iz grafa enega nedoločenega integrala dobimo grafe vseh ostalih nedoločenih integralov izbrane funkcije ? Grafe vseh dobimo iz enega izmed njih z vzporednimi premiki za vektor . Grafe vseh dobimo iz enega izmed njih z vzporednimi premiki za vektor . Grafe vseh dobimo iz enega izmed njih s premiki za vektor .
Rešitev
Vsi nedoločeni integrali so oblike , kjer je . Med seboj se razlikujejo v aditivni konstanti . Grafe vseh dobimo iz enega izmed njih z vzporednimi premiki za vektor .
Rešitev
Vsi nedoločeni integrali so oblike , kjer je . Med seboj se razlikujejo v aditivni konstanti .
Rešitev
Grafe vseh dobimo iz enega izmed njih z vzporednimi premiki za vektor .
Primeri grafov
Grafi funkcij (moder), (rdeč) in (zelen).
Narobe
Zmotil si se pri obeh izbirah.
Poskusi ponovno.
Narobe
Zmotil si se pri prvi izbiri.
Poskusi ponovno.
Narobe
Zmotil si se pri drugi izbiri.
Poskusi ponovno.
Pravilno
Dodatne naloge
Rešitev
a)
b)
c)
Narobe
Pravilno si izbral od treh odgovorov
Poskusi ponovno.
Pravilno
Dodatne naloge
Dokaz
Zvezo dokažemo z odvajanjem funkcije F:
