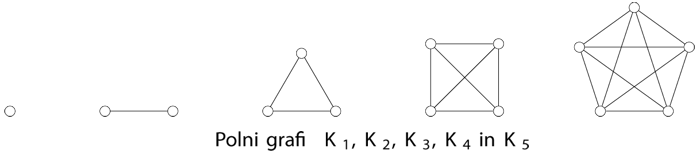
Naj bo (običajno končna) neprazna množica in poljubna družina dvoelementnih
podmnožic množice . Paru pravimo graf na množici točk (tudi vozlišč) in z množico povezav . Če je povezava grafa , tedaj pravimo, da sta točki in sosednji in pišemo . Hkrati pravimo, da sta točki in krajišči povezave . Povezavo včasih pišemo krajše kot ali .
OPOMBA
Včasih dopuščamo tudi grafe, ki imajo med nekaterimi pari točk več povezav (vzporedne povezave) ali pa imajo povezave, ki imajo obe krajišči enaki (zanke). Takim grafom bomo rekli multigrafi. Če definiramo, da zanka prispeva k stopnji točke, potem lema 1.1 velja tudi za multigrafe. Kadar želimo poudariti, da govorimo o (multi)grafih brez zank in vzporednih povezav, takim grafom rečemo enostavni grafi.
Poleg multigrafov je grafom sorodna stuktura usmerjeni graf. Neformalno si ga lahko predstavljamo kot graf (ali celo kot multigraf), kjer vsako povezavo usmerimo. Namesto krajišč povezave v tem primeru govorimo kot o začetku in koncu povezave (repu in glavi povezave).
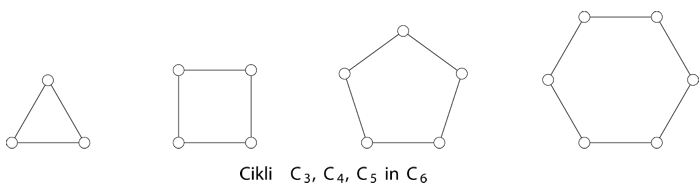
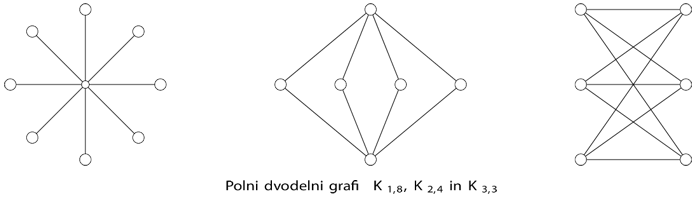
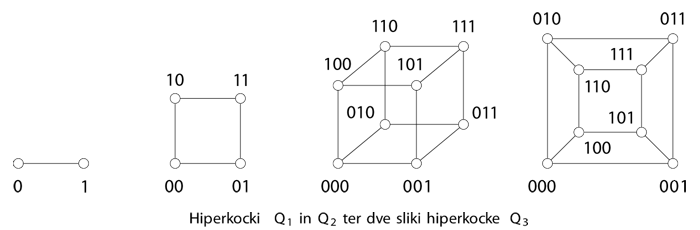
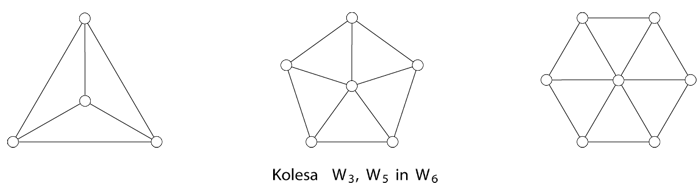
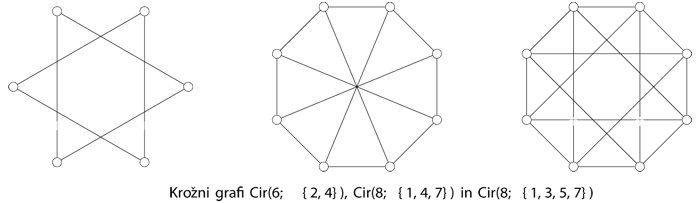
Grafe si radi tudi narišemo. To storimo tako, da vozlišča grafa predstavimo kot točke ravnine, povezavo med sosednjima vozliščema pa kot krivuljo (običajno kar kot daljico) s krajiščema v točkah ravnine, ki ustrezata krajiščema povezave.
Stopnja točke (tudi valenca točke) v grafu , označimo jo z , je enaka številu povezav grafa , ki imajo točko za svoje krajišče. Točkam stopnje pravimo izolirane točke. Graf je regularen, če obstaja tako število , da velja za vsak . V tem primeru rečemo tudi, da je graf -regularen, oziroma, da je regularen stopnje .