Povedati moramo še, kaj so racionalna števila. Racionalno pomeni v razmerju. Izraz izhaja iz grščine še iz časov, ko so verjeli, da se da vse izraziti s celoštevilskimi razmerji. Zato racionalno dejansko pomeni v celoštevilskem razmerju.
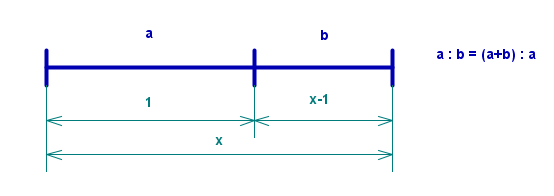
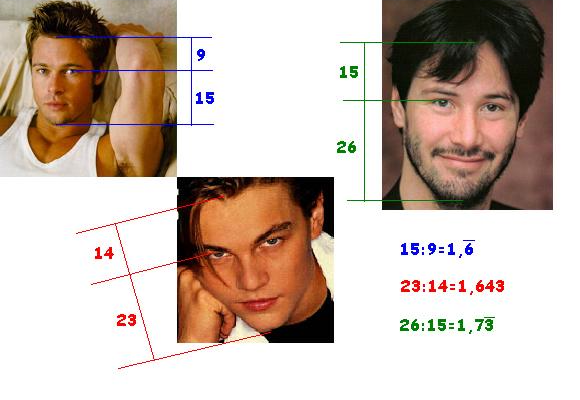
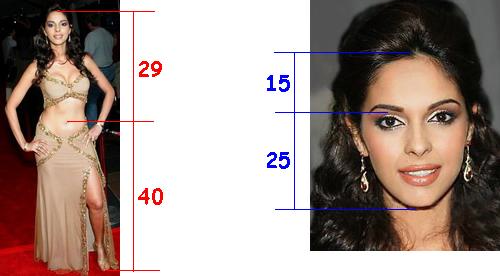
Danes smo si ogledali različna razmerja. Najprej smo opazovali razmerje med dolžinama dveh daljic. Opazovali smo le daljice s celoštevilskimi dolžinami, torej smo dobili racionalna razmerja. Nato smo precej podrobno spoznali zlati rez. Ugotovili smo, da je to razmerje predstavljeno s številom
V števcu je koren iz pet, ki ni celo število. Tega ulomka nikakor ne moremo preoblikovati tako, da bi bila števec in imenovalec celoštevilska. Zlati rez zato ni racionalno razmerje.
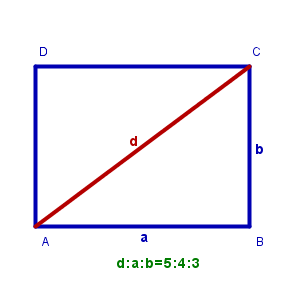
Sledil je skok v geometrijo. Najprej smo ugotovili, da je razmerje med obsegom in premerom kroga konstantno in enako številu . Tudi tega števila ne moremo zapisati s celoštevilskim ulomkom; taki ulomki so le njegovi približki (omenili smo ), zato je tudi razmerje med obsegom in premerom kroga iracionalno. Enako je pri razmerju med diagonalo in stranico kvadrata. Za razmerje v pravokotniku pa smo že pri konstrukciji napisali, kdaj je celoštevilsko, to je racionalno.
Kasneje bomo videli, da racionalno število predstavlja razmerje dveh soizmerljivih količin. Količini sta soizmerljivi, če obstaja neka dolžinska enota, s katero lahko izmerimo obe. Na primer: dve palici sta soizmerljivi, če obstaja neka tretja palica, s katero lahko izmerimo obe (tako da se izide). Racionalno število običajno zapišemo z ulomkom s celoštevilskim števcem in imenovalcem. O tem bomo še govorili.