Prestavi točke
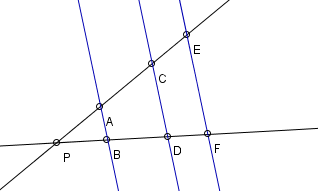
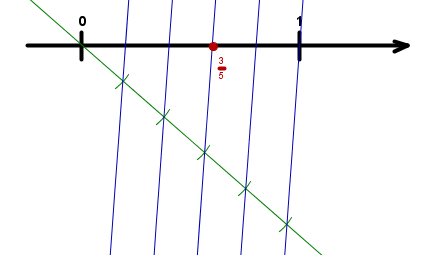
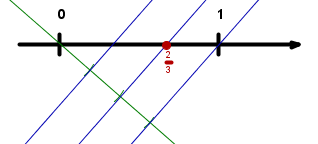
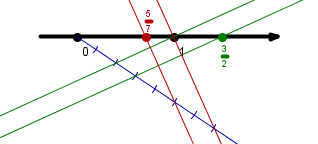
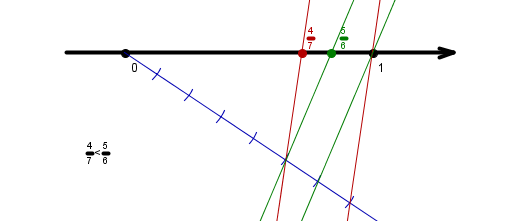
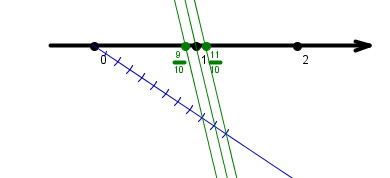
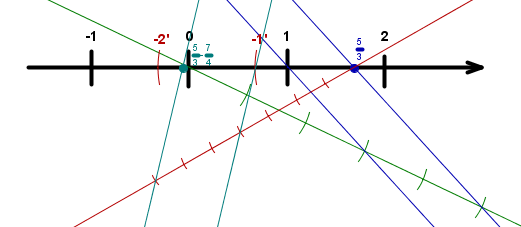
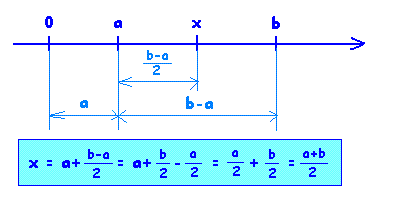
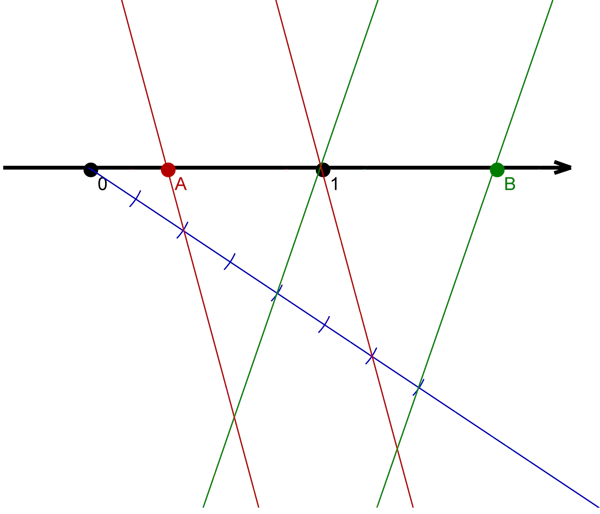
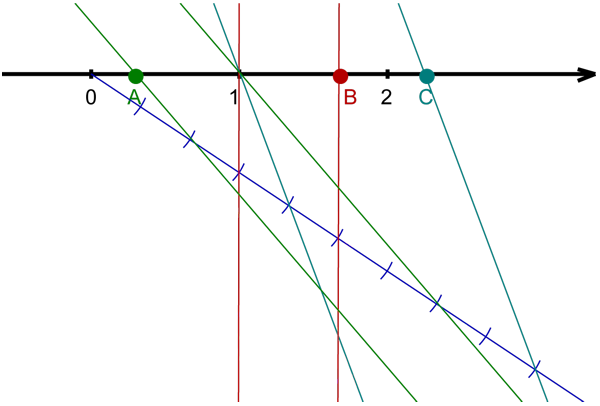
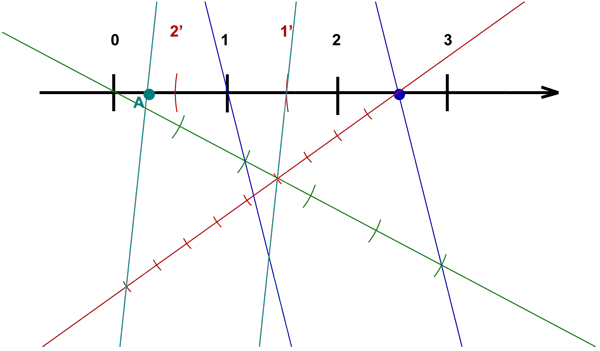
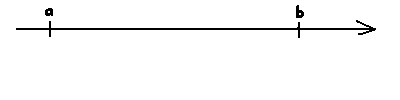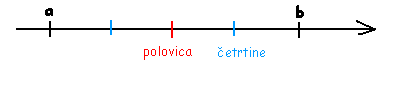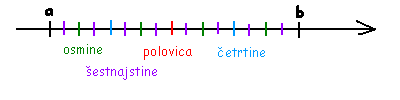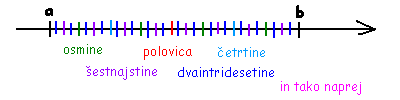Točke , , in prestavi na številsko os tako, da bodo po vrsti predstavljale , , in .
Kako ti je šla uvodna naloga? Če ulomke zapišeš v obliki s celim delom, postane naloga prav lahka, saj je vse že pripravljeno – ustrezne daljice so razdeljene na ravno pravo število enakih delov. Spomnimo se, da racionalni ulomek (števec in imenovalec sta celi števili) pove, na koliko enakih delov je razdeljena celota (imenovalec) in koliko takih delov vzamemo (števec).
Risanje ulomkov
Vendar to še ni naš cilj. Ulomke želimo narisati. Nekaj smo jih že narisali. Tokrat poskusimo malo drugače. Pri risanju smemo uporabljati le neumerjeno ravnilo in šestilo. Kako bi s takim orodjem narisali ulomek? Pomagali si bomo s Talesovim izrekom, ki pravi naslednje:
Če imamo dve sekajoči se premici in dve vzporednici, kot je na sliki spodaj, je razmerje odsekov na eni premici enako razmerju enakoležnih odsekov na drugi od premic, ki se sekata.
Uporaba Talesovega izreka pri risanju
In kako bomo Talesov izrek uporabili pri našem risanju? Narisali bomo pomožno premico in na njej s šestilom odmerili nekaj enakih delčkov. Nato bomo z vzporednicami enoto razdelili na enake dele. Narišimo si sliko za petine in nato označimo ulomek .
Tako, zdaj smo zreli za prvo čisto pravo konstrukcijo. Hitro pripravi ravnilo in šestilo. Skonstruiraj ulomek . Ker je imenovalec tri, moraš enoto razdeliti na tri enake dele.
1. naloga
Na spodnji sliki točko, ki predstavlja enoto, prestavi tako, da bo točka predstavljala ulomek . Nato jo prestavi še tako, da bo točka predstavljala ulomek . Ko bo enota na pravem mestu, se bo izpisal ustrezen ulomek.
2. naloga
Skonstruiraj še in .
3. naloga
Sedaj skonstruiraj še in .
Izberi, kateri ulomek predstavlja večje število.
Pravilno!
je desno od , zato je oziroma .
Narobe.
je desno od , zato je oziroma . Naprej
4. naloga
Pravilno!
Vsota dveh racionalnih števil je racionalno število.
Narobe.
Vsota dveh racionalnih števil je racionalno število.
Pravilno!
Narobe.
Pravilno!
Narobe.
Ali sta in racionalni števili?
Seštevanje in odštevanje na številski premici
Poskusimo narisati še vsoto in razliko dveh ulomkov. Začnimo z vsoto, skonstruirajmo
|
| Kaj se dogaja na sliki? Ulomek že znamo narisati. S tem se začne. Nato se iz slike za po istem postopku, kot bi risali iz izhodišča, nariše ulomek . Dobljena točka je slika iskane vsote. |
Risanje razlike
Vidimo, da vsote dveh ulomkov ni težko narisati, le dve sliki moramo združiti. Kako bomo pa narisali razliko? Zelo podobno, le da bomo morali drugi ulomek narisati v drugo, negativno smer. Poskusi narisati
Kako smo prišli do iskane točke? Najprej smo narisali ulomek , nato smo iz te točke narisali v negativno smer (kot bi risali iz izhodišča) in tako dobili točko, ki predstavlja dano razliko.
Gostota racionalnih števil
Za konec povejmo nekaj besed o gostoti racionalnih števil na številski premici. Strokovnjaki pravijo: racionalna števila so povsod gosta. To pomeni, da je na vsakem, še tako majhnem koščku številske premice neskončno mnogo racionalnih števil.
In kako bi to lahko preverili? Vzemimo košček številske premice (uradno se temu reče interval) in na njem narišimo dve racionalni števili. Katero število je točno na sredini med njima? Iz spodnje slike je razvidno, da je iskano število
Velja
Če sta in racionalni števili, je tudi zgornje število racionalno, saj sta vsota in produkt dveh racionalnih števil racionalni števili. Tako smo ugotovili, da je točno na sredini med dvema racionalnima številoma racionalno število. Na intervalu je zato neskončno racionalnih števil. Racionalna števila so na mejah, na polovici, na četrtinah (sredina polovic), na osminah (sredina četrtin), na šestnajstinah (sredina osmin) in tako naprej. Polovic nam nikoli ne zmanjka in tako dobimo neskončno racionalnih števil.
1. naloga
Pravilno!
, , , ,
Narobe.
, , , ,
2. naloga
Pravilno!
,
Narobe.
,
3. naloga
Nariši točke , in , ki po vrsti predstavljajo ulomke , in .
4. naloga
Nariši točko , ki predstavlja .
Rezultati
