Spomni se pretvarjanja med metri, centimetri, decimetri, milimetri in kilometri. V tabelo vpiši manjkajoče podatke.
kg = m
m = cm
m = mm
km = cm
km = mm
Merske enote
Spomni se pretvarjanja med metri, centimetri, decimetri, milimetri in kilometri. V tabelo vpiši manjkajoče podatke.
kg = m
m = cm
m = mm
km = cm
km = mm
Rešitev je pravilna!
Rešitev ni pravilna!
kg = 1000 m
m = 10000 cm
m = 100 mm
km = 1000000 cm
km = 10000000 mm
Primer
Če bi želeli zapisati, koliko milimetrov je km, bi dobili veliko ničel.
Izberi, katera od podanih možnosti je pravilna:
km = 1.000.000 1.000.000.000.000 1.000.000.000 1.000.000.000.000.000 1.000 mm
Rešitev je pravilna!
Zaradi velikega števila ničel si pomagamo s potencami. Število lahko zapišemo kot produkt samih :
Rešitev je napačna!
Zaradi velikega števila ničel si pomagamo s potencami. Število lahko zapišemo kot produkt samih :
Reši sam
Kako zapišemo število s potenco? Izberi pravilno rešitev za potence.
Število zapišemo kot:
Število zapišemo kot:
Rešitev je pravilna!
Rešitev je napačna!
Kaj je potenca?
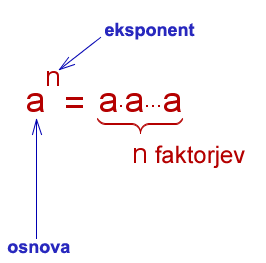
Poskusi
Naslednje primere poskusi rešiti sam.
1. Zapis z eno samo potenco je: | 4. Zapis z eno samo potenco je: |
2. Zapis kot produkt dveh potenc je: | 5. Zapis kot ulomek dveh potenc je: |
3. Zapis samo z enim eksponentom je: |
Rešitev je pravilna!
Pravila in lastnosti
Pri računanju s potencami si pomagamo z naslednjimi pravili:

1. primer
Bi znal pravila uporabiti v naslednjih primerih?
Zapis samo z enim eksponentom je:
Katero pravilo si uporabil zgoraj?
Koliko so , , in ?
Rešitev je pravilna!
Rešitev je napačna!
Uporabil si prvo pravilo, in sicer množenje potenc. Vrednosti posameznih parametrov so:
,
,
.
Parameter b v tem primeru ne nastopa.
2. primer
Rešitev je pravilna!
Rešitev ni pravilna!
Uporabiš četrto pravilo za deljenje potenc oziroma za ulomke in dobiš: . Vrednosti parametrov so:
,
,
.
Parameter b tudi v tem primeru ne nastopa.
3. primer
Rešitev je pravilna!
Rešitev ni pravilna!
Uporabil si pravilo drugo pravilo, kjer gre za potenciranje produkta.
Vrednosti parametrov so:
,
,
.
Ali so izjave pravilne?
Rešitev je pravilna!
To pa ne bo držalo!
Kratek primer
Na spodnjem apletu je prikazana uporaba četrtega pravila na primeru . S klikom na puščico v levo si ogledaš posamezne korake.
Seveda lahko ulomek krajšaš in dobiš . Če primerjaš zadnja rezultata, vidiš, da je . Izračunajmo . Uporabimo prvo pravilo za množenje potenc. Dobimo . Enakost lahko zapišemo nekoliko drugače: .
Bi znal sam izraziti na podoben način? Kaj dobiš?
Rešitev je pravilna!
To pa ne bo držalo!
Podobno kot zgoraj velja:
Zapomni si:
1. primer
Rešitev je pravilna!
To pa ne bo držalo!
Uporabi enakost .
2. primer
Rešitev je pravilna!
To pa ne bo držalo!
Uporabi lastnost .
3. primer
Rešitev je pravilna!
To pa ne bo držalo!
Združi znanje iz zgornjih primerov.
4. primer
Rešitev je pravilna!
To pa ne bo držalo!
Upoštevaj vrstni red operacij in znanje iz zgornjih primerov.
5. primer
Rešitev je pravilna!
To pa ne bo držalo!
Najprej odpravi oklepaje, nato , in zapiši kot potence z isto osnovo ter upoštevaj pravilo za množenje potenc.
Ali držijo naslednje izjave?
Razmisli, ali je pravilno.
Razmisli, ali je pravilno.
Rešitev je pravilna!
To pa ne bo držalo! Vsaj en odgovor je napačen.
je pravilno, je napačno, saj je , ker je .
Poenostavi
Spodnji primer povezuje uporabo vseh pravil za računanje s potencami. Vsak posamezen korak svoje rešitve lahko preveriš s klikom na gumb za naprej.
Izpostavi skupni faktor
V naslednjem računu izpostavimo skupni faktor in zapišimo rezultat kot potenco.
Vidimo, da lahko tudi v primerih, ko neznanka nastopa v eksponentu, uporabljamo pravila za potence.
Še en primer
Izpostavi skupni faktor in poskusi naslednji primer rešiti sam. Za pomoč si lahko s klikom na gumb za naprej ogledaš posamezne korake rešitve.
Preveri svoje znanje
Rešitev je pravilna!
Preveri svoje znanje
Rešitev je pravilna!
1. naloga
Rešitev je pravilna!
1. naloga
Rešitev je pravilna!
2. naloga
1. Skrči izraz , kolikor je mogoče. Kaj dobiš?
2. Skrči izraz , kolikor je mogoče. Kaj dobiš?
3. Skrči izraz , kolikor je mogoče. Kaj dobiš?
Rešitev je pravilna!
3. naloga
1. Skrči izraz , kolikor je mogoče. Kaj dobiš?
2. Skrči izraz , kolikor je mogoče. Kaj dobiš?
3. Skrči izraz , kolikor je mogoče. Kaj dobiš?
Rešitev je pravilna!
4. naloga
1. Izrazu izpostavi skupni faktor ter izračunaj. Katero rešitev dobiš?
2. Izrazu izpostavi skupni faktor ter izračunaj. Katero rešitev dobiš?
3. Izrazu izpostavi skupni faktor ter izračunaj. Katero rešitev dobiš?
Rešitev je pravilna!
Rezultati