Dano je omrežje utežno usmerjenih povezav:

omrežje3

Denimo, da nas zanimajo najkrajše poti iz izhodiščnega vozlišča 0. Na naslednjih straneh si bomo ogledali vrsto vprašanj s katerimi bomo utrdili naše poznavanje Bellman-Ford-ovega algoritma, ki nam pomaga pri iskanju najkrajših poti iz izhodiščnega vozlišča do ostalih volišč.

enojno povezani graf: če obstaja povezava iz v potem ne obstaja povezava iz v .
poln graf: če vsebuje vse možne povezave.

OPTIMALNI PREDHODNIK (NA KONKRETNEM PRIMERU):
Dano imamo optimalno pot iz v : -> -> -> -> .
Velja:
je optimalni predhodnik vozlišča ,
je optimalni predhodnik vozlišča ,
je optimalni predhodnik vozlišča in
je optimalni predhodnik vozlišča .

Ali je optimalna pot iz v posredna ali neposredna?

omrežje3

Zakaj nebi morala potekati pot skozi točko ?

omrežje3

Koliko manjka povezav, da bi bil graf poln, če imamo opravka z enojno povezanim grafom ?

omrežje3

Kolikšna je optimalna pot iz v in iz koliko povezav sestoji optimalna pot?

omrežje3

Katero je predhodno vozlišče vozlišča , ko gre za optimalno pot iz vozlišča ?

omrežje3

Katere vrednosti zavzamejo dolžine točke , katerih poti potekajo do te točke, če rešujemo problem preko Bellman-Ford algoritma in vemo, da algoritem sprejme množice uteženih usmerjenih povezav v naslednjem vrstnem redu:
.

omrežje3

REŠITEV V OBLIKI FILMČKA

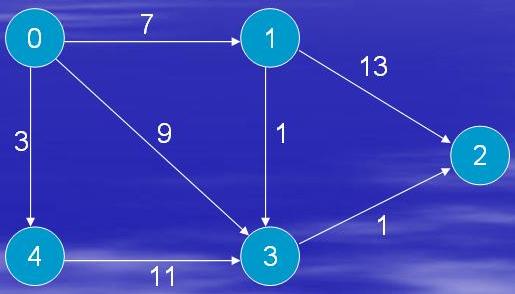
Kolikokrat moramo skozi vse povezave v grafu , da pridemo do optimalne poti iz do preko Bellman-Ford algoritma in pri kateri uteženi usmerjeni povezavi se to zgodi?
Vemo, da algoritem sprejme množice uteženih usmerjenih povezav v naslednjem vrstnem redu:
.
Opišite postopek reševanja!

omrežje3

REŠITEV Z OPISOM POSTOPKA REŠEVANJA:

Ko gremo PRVIČ skozi vse povezave:

Povezava (0,1,7): Pot iz 0 v 1 dobi vrednost 7.

Povezava (0,4,3): Pot iz 0 v 4 dobi vrednost 3.

Povezava (0,3,9): Pot iz 0 v 3 dobi vrednost 9.

Povezava (4,3,11): Če povezavi (0,4) dodamo povezavo (4,3) dobimo slabšo pot kot pa če gremo iz 0 neposredno v 3 (3+11=14 > 9).

Povezava (1,3,1): Če povezavi (0,1) dodamo povezavo (1,3) dobimo boljšo pot kot pa če gremo iz 0 neposredno v 3 (7+1=8 < 9). To je naš optimum.

Torej moramo iti manj kot enkrat skozi vsa vozlišča. Do želene rešitve pridemo pri povezavi (1,3,1) in naša optimalna vrednost je 8.

Ali se spremeni optimalna pot od točke do , če odstranimo (uteženo) povezavo ?
Če se, kolikšna je nova vrednost?

omrežje3

Ali se spremeni optimalna pot od točke do , če dodamo (uteženo) povezavo
Če se, kolikšna je nova vrednost?

omrežje3

V samem javanskem programu Bellman-Ford bi lahko pri prvem koraku množici (dolžine najkrajših poti od izhodiščne točke do vseh vozlišč) nastavili začetne vrednosti Integer.MAX_VALUE (največje možno celo število, ki ga pozna java).

Preveri

Dano je omrežje:

omrežje1

Kolikšne so dolžine najkrajših poti od izhodiščnega vozlišča do vozlišč in .
Odgovor zapišite v obliki: 0 3 4 -1 4

Preveri

Dano je omrežje:

omrežje1

Kdo je optimalni predhodnik vozlišča ?

Kolikokrat moramo skozi vse povezave, da pridemo do optimalne rešitve preko Bellman-Ford algoritma, če je število vozlišč enako ?

Dano je omrežje:

omrežje2

Kolikšna je najkrajša pot od vozlišča do vozlišča ?

Preveri