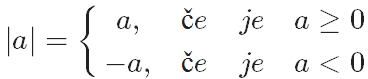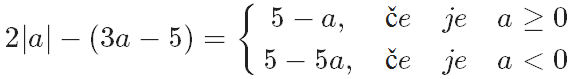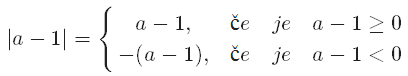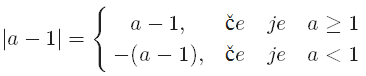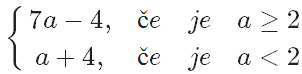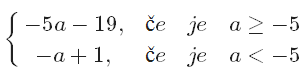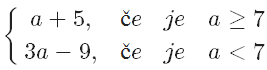Enačba
S pomočjo naslednjega apleta reši enačbo . Rdeči drsnik določa polmer krožnice. Premikaj ga levo in desno in tako spreminjaj velikost krožnice. Ko boš našel pravi rešitvi, se bo prikazal napis "Bravo". Dobljeni rešitvi tudi zapiši.
Enačba ima dve rešitvi, in sicer in , saj je absolutna vrednost obeh števil res .
Enačba
Na spodnjem apletu so prikazane rešitve poljubne enačbe . Število spreminjaš s premikanjem drsnika levo in desno.
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
in
Super, rešitev je pravilna.
To pa ne bo držalo.
Enačba nima rešitve.
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Razmisli
Bi znal rešiti enačbo .
Spomni se, da velja .
Enačba se tako glasi: .
Deliš jo z in dobiš .
Rešitvi te enačbe že poznaš: in
Kadar rešujemo enačbo imamo tri možnosti:
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
in
Super, rešitev je pravilna.
To pa ne bo držalo.
Enačba nima rešitve.
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
in
Grafični pristop
Na spodnjem apletu je prikazan grafičen način reševanje enačbe . Z modro je narisan graf . Premica je narisana z rdečo barvo in jo lahko premikaš s pomočjo zelene točke. Zraven se izpišeta rešitvi enačbe, če obstajata.
Primeri
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
in
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
in
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
in
Razdalja
Ali si opazil, da je ravno razdalja med številoma in . Kaj pa razdalja med številoma in ? Tudi ta razdalja je . Podobno kot je razdalja od Ljubljane do Maribora enaka razdalji od Maribora do Ljubljane, sta razdalji med številoma in ter številoma in enaki.
Razdalja med številoma in je . Izračunamo jo lahko kot ali . Podobno je tudi razdalja med in enaka .
V tretjem primeru smo računali razdaljo med številoma in . Ta razdalja je enaka . Razmisli, zakaj jo lahko izračunamo tudi kot .
Razdaljo v prvem in drugem primeru smo dobili tako, da smo števili odšteli in vse skupaj dali v absolutno vrednost. V tem primeru imamo števili in . Po eni strani je razdalja enaka . Lahko pa zamenjamo in dobimo , kar je isto kot .
Razdalja na premici
Premikaj točki, ki predstavljata števili in , ter opazuj spreminjanje razdalje med točkama. Razdaljo predstavlja rdeča daljica in je označena z .
Ali drži trditev?
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Pravilno, saj velja .
Primera
1. Rešimo enačbo: .
Vemo, da je razdalja med številoma in . Iščemo vsa števila, ki so od oddaljena za .
To pa sta števili: in .
2. Poskusimo rešiti enačbo:
Tu gre za podoben trik kot v zadnjem primeru zgoraj: je isto kot . Enačba nam pove, koliko je oddaljen od števila . V tem primeru gre za razdaljo enot, torej sta to števili in .
Enačba
Ko rešujemo enačbo , iščemo števila, ki so od točke oddaljene za . Premikaj drsnika za in levo-desno, ter opazuj kako se spreminja enačba in njeni rešitvi.
Super, rešitev je pravilna.
To pa ne bo držalo.
Rešitvi sta in . Obe števili za enoto oddaljeni od števila .
Super, rešitev je pravilna.
To pa ne bo držalo.
Rešitvi sta in . Števili za enoti oddaljeni od števila .
Super, rešitev je pravilna.
To pa ne bo držalo.
Rešitvi sta in .
Reši sam 1
Super, rešitev je pravilna.
To pa ne bo držalo.
Rešitev je ena sama: , saj mora biti razdalja .
Super, rešitev je pravilna.
To pa ne bo držalo.
Rešitev ne obstaja, saj razdalja in s tem tudi absolutna vrednost ne more biti negativna.
Naloga
Rešimo še enačbo:
Upoštevamo lastnosti absolutne vrednosti: .
Rešiti je potrebno: .
Delimo z : .
Rešitvi te enačbe sta: in .
Reši enačbo:
Super, rešitev je pravilna.
To pa ne bo držalo.
Podobno kot zgoraj:
Rešiti je potrebno enčabo:
Deliš s :
Rešitvi sta in .
Obravnava izrazov
Obravnavajmo izraz .
Ločiti moramo dve možnosti, ki sta posledici enačbe za absolutno vrednost:
Do konca znaš izračunati sam. Končno rešitev lahko zapišemo:
Obravnavaj izraz
Obravnavaj izraz . Upoštevaj definicijo absolutne vrednosti. Pod prvim gumbom se skriva namig, pod drugim pa rešitev.
Namig:
Zgornji namig lahko zapišeš malo drugače:
Zopet ločimo 2 možnosti:
Obravnava enačb
Bi znali rešiti enačbo: ?
Podobno kot pri obravnavi izrazov upoštevamo, definicijo absolutne vrednosti: je , ko je negativen, oziroma je , če je pozitiven.
To najlažje rešimo v dveh delih:
1) Naj bo pozitiven. Enačba bo tako enaka: .
Dobimo in .
2) Če je negativen, je začetna enačba enaka: .
Torej . Rešitev je
Super, rešitev je pravilna.
To pa ne bo držalo.
Ločimo dve možnosti.
1) Naj bo pozitiven, torej je .
Enačba se spremeni v:
Dobiš in .
2) Če je negativen, je .
Začetna enačba izgleda takole: .
Torej . Rešitev je .
Super, rešitev je pravilna.
To pa ne bo držalo.
Zopet ločimo dve možnosti, vendar je potrebno pogledati, kdaj je pozitivno oziroma negativno število. Torej nas zanimata možnosti, ko je večji od oziroma manjši od .
1) Naj bo večji od .
je pozitivno število, zato je .
Enačba se glasi .
Dobimo , torej .
2) Naj bo manjši od . je sedaj negativno število, zato je .
Enačba je kar taka: .
Odpravimo oklepaje: .
Dobimo , torej .
Koliko si si zapomnil?
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
in
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
in
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Enačba nima rešitve.
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
in
1. naloga
Izračunaj razdaljo med številoma na številski premici.
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
| Razdalja med in . | |
| Razdalja med in . | |
| Razdalja med in . | |
| Razdalja med in . |
2. naloga
Reši enačbe in ustrezno poveži.
Super, rešitev je pravilna.
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Super, rešitev je pravilna.
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Super, rešitev je pravilna.
5. naloga
Reši enačbe in ustrezno poveži.
Super, rešitev je pravilna.
Rezultati
