Neenačbe in |x|
Ponovi
Odlično, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Pravilno.
Odlično, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Nepravilno.
Odgovor na vprašanje
Števila, ki ležijo znotraj kroga s polmerom , ustrezajo neenačbi . Na spodnji simulaciji lahko z drsnikom spreminjaš polmer krožnice. Točke, ki ležijo na krožnici ali znotraj nje, so od izhodišča oddaljene kvečjemu za (polmer). Torej ustrezajo neenačbi: .
S premikanjem drsnika levo-desno poišči točke, ki so največ za enote oddaljene od izhodišča.
Ob tem lahko opazuješ spreminjanje neenačbe in kaj se dogaja z rešitvijo za različne vrednosti . Rešitev je obarvana z modro.
Odgovor na vprašanje
Števila, ki so od izhodišča številske premice oddaljena za največ enote, lahko zapišemo z intervalom .
Ta števila ustrezajo neenačbi .
Na prejšnjem apletu si videl:
Števila, ki so od izhodišča oddaljena za največ enot so rešitve neenačbe: oziroma ustrezajo tej enakosti.
Če točki, ki ležita na krožnici, odstranimo, iščemo števila, ki so od izhodišča oddaljena za manj kot . Neenačba se v tem primeru glasi: .
Reši 1
Poišči rešitve spodnjih neenačb in jih ustrezno poveži.
Odlično, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
| Absolutna vrednost ne more biti negativna. | |
| Števila, ki so do izhodišča oddaljena za največ pol enote. |
Zapomni si
Iz prejšnjih primerov lahko zaključimo naslednje.
Neenačba :
- nima rešitve, če je negativno število;
- ima samo eno rešitev, če je , in ta rešitev je ;
- ima neskončno rešitev, če je pozitivno število, in ta rešitev je interval .
Podobno velja za neenačbo :
- nima rešitve, če je negativno število ali ;
- ima neskončno rešitev, če je pozitivno število, in ta rešitev je interval .
Oddaljenost od izhodišča za več kot
Kaj pa, če iščeš števila, ki so od izhodišča oddaljena za več kot enot?
Ta števila pa res ležijo zunaj kroga s polmerom .
S premikanjem drsnika levo-desno se spreminja ta neenačba in njena rešitev, ki je prikazana z modro barvo.
Reši 2
Odlično, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
| Kateri neenakosti ustrezajo števila, ki so od izhodišča oddaljena za več kot 2 enoti? | |
| Kateri neenakosti ustrezajo števila, ki so od izhodišča oddaljena za najmanj 3 enote? | |
| Poišči rešitev neenačbe: | |
| Poišči rešitev neenačbe: | |
| Poišči rešitev neenačbe: | Absolutna vrednost je vedno nenegativna, zato so rešitev kar vsa števila. |
Povzetek
Podobno kot prej lahko iz prejšnjih primerov zaključimo takole.
1) Neenačbo :
- reši vsako število, če je negativno število;
- reši vsako število razen , če je , in ta rešitev je ;
- reši neskončno števil, če je pozitivno število, in ta rešitev je .
2) Neenačbo :
- reši vsako število, če je negativno število ali je ;
- reši neskončno števil, če je pozitivno število, in ta rešitev je .
Kaj pa če nismo v izhodišču?
Spodnja simulacija prikazuje rešitev neenačbe: . Kadar rešuješ takšno neenčbo, iščeš takšne točke, ki so od točke oddaljene za manj kot enot.
Na razpolago imaš dva drsnika za in . Premikaj ju levo-desno ter opazuj spreminjanje neenačbe in njeno rešitev, ki je obarvana modro.
Reši 3
Odlično, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Odlično, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Odlično, rešitev je pravilna.
To pa ne bo držalo.
Absolutna vrednost ne more biti negativna, zato enačba nima rešitve.
Ali velja?
Razmisli, ali veljajo naslednje trditve in ustrezno poveži.
Odlično, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
| Rešitev neenačbe je število . | Pravilno. Samo število –2 je za največ 0 enot oddaljeno od –2. |
| Števila, ki so za manj kot enote oddaljena od števila , so rešitev neenačbe . | Nepravilno. Ustrezna neenakost je . |
Naloga
Poišči rešitev neenačbe: oziroma množico točk, ki so za manj kot enote oddaljene od števila .
1. Najprej moraš točno postaviti rdečo piko, ki predstavlja število . Ko je ta točka dobro postavljena, se zapolni srednja izmed treh praznih rdečih kroglic.
2. Modri piki predstavljata krajišči iskane množice. Ko stojita na pravih mestih, se zapolnita tudi drugi dve rdeči kroglici.
3. Ko izbereš pravo množico, se pojavi napis Bravo.
Rešitev zgornje neenačbe zapisana z intervalom:
Enačba
Spodnja slika prikazuje rešitev neenačbe: .
Velja, da neenačba:
- nima rešitve, če je negativno število ali je ;
- ima neskončno rešitev, če je pozitivno število, in ta rešitev je interval .
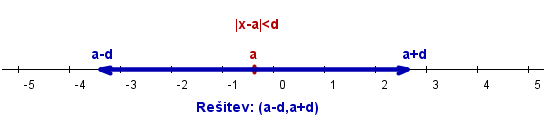
Velja pa tudi, da neenačba :
- nima rešitve, če je negativno število ali je ;
- ima neskončno rešitev, če je pozitivno število, in ta rešitev je interval .
Enačba
Spodnja slika prikazuje rešitev neenačbe: .
Neenačbo:
- reši vsako število, če je negativno število;
- reši vsako število razen , če je , in ta rešitev je ;
- reši neskončno števil, če je pozitivno število, in ta rešitev je .
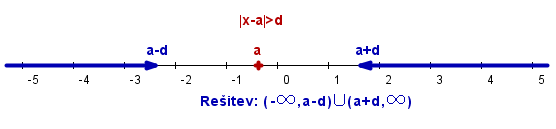
Podobno velja, da neenačbo :
- reši vsako število, če je negativno število ali je ;
- reši neskončno števil, če je pozitivno število, in ta rešitev je .
Grafični pristop
Podobno kot enačbe lahko tudi neenačbe rešujemo grafično. Spodaj sta narisana graf in premica , ki jo lahko z rjavo točko prestavljaš dol oziroma gor.
Z zeleno je prikazana rešitev neenačbe: . Rešitve takšnih neenačb vedno obstajajo.
Z modro pa je prikazana rešitev neenačbe: . Taka neenačba nima vedno rešitve.
Primer
1. Rešimo neenačbo .
Spomnimo se .
Dobimo neenačbo: .
Delimo s : .
Rešitev so vsa števila, ki so od številla oddaljena za manj kot enote: .
2. Rešimo neenačbo .
Začnemo podobno kot zgoraj: .
Dobimo neenačbo: .
Delimo z : . Spomni se tudi trika:
Iščemo torej števila, ki so od oddaljena za več kot enote.
1. naloga
Reši neenačbe in ustrezno poveži.
Odlično, rešitev je pravilna.
2. naloga
Reši neenačbe in ustrezno poveži.
Odlično, rešitev je pravilna.
3. naloga
Reši neenačbe in ustrezno poveži.
Odlično, rešitev je pravilna.
Rezultati