No pa si poglejmo še nekaj primerov grafov ter poiščimo hamiltonove cikle, če obstajajo.
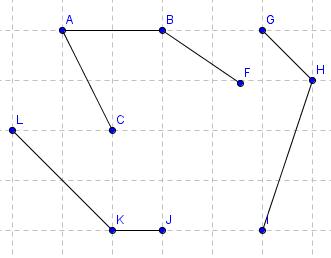
- 1. naloga Dan je graf:
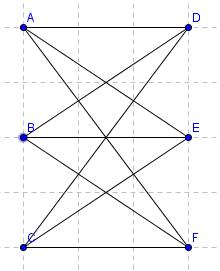
Ali je hamiltonov?
Kot že vemo, nekega postopka za ugotovitev hamiltonosti grafa ni. Najdemo ga s poskušanjem.
Hamiltonov cikel - vaje
No pa si poglejmo še nekaj primerov grafov ter poiščimo hamiltonove cikle, če obstajajo.

Ali je hamiltonov?
Kot že vemo, nekega postopka za ugotovitev hamiltonosti grafa ni. Najdemo ga s poskušanjem.
Hamiltonov cikel - vaje
Izberemo si poljubno točko, naj to to točka C. Potujemo do točke D, nato do točke A, nato do E:
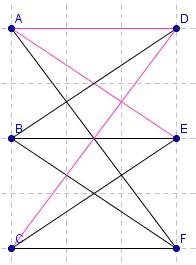
Kot vidimo, imamo iz točke E dve možnosti: pot lahko nadaljujemo v točko B ali v točko C. Vendar smo točko C že obiskali, to je naša začetna točka. Na koncu bomo sicer zaključili v C, če cikel obstaja, vendar zdaj še ne zato, ker nismo obiskali vseh vozlišč! Nadaljujemo v točko B, iz B v F ter iz F v končno točko C. Pot, označena z roza barvo je povezana, vsa vozlišča smo obiskali le enkrat, torej je graf hamiltonov.
Hamiltonov cikel - vaje
In še slika hamiltonovega cikla:
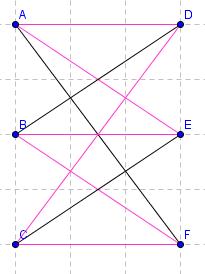
Spomnimo se, da smo v teoriji omenili dva izreka. Tukaj bi lahko porabili Orejev izrek, ki pravi, da če je vsota dveh nesosednjih točk večja ali enaka vsoti vseh točk v grafu, potem je graf hamiltonov. Pogledamo recimo točki C in A. Vozlišče A je stopnje 3, prav tako vozlišče C. Torej je vsota stopenj 6. In to je enako 6, ki je število vseh vozlišč v grafu.
Hamiltonov cikel - vaje
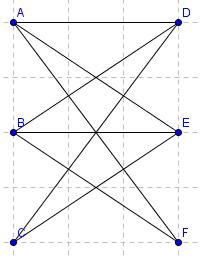
Pa si za začetno točko spet izberimo točko C. Potujemo do točk D, A, F, nato do B, E, ter v začetno točko C. Torej je tudi ta graf hamiltonov. Še slika:
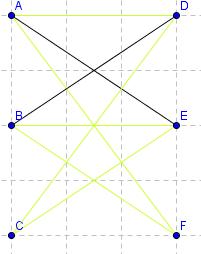
Hamiltonov cikel - vaje
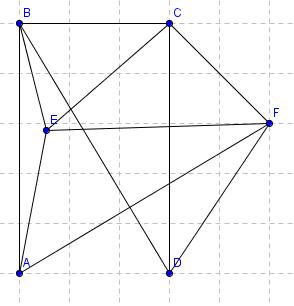
No pa uporabimo npr. Diracov izrek. Vsota vseh vozlišč v grafu je 6. Poiščemo točko z najmanjšo stopnjo in vidimo, da je to stopnja 3, kar je enako polovici vseh vozlišč. Torej je po izreku ta graf hamiltonov. Poiščimo še hamiltonovo pot: Začnimo v tč.A, nadaljujemo do B, nato do D, nato do C, preko tč. F do E ter v začetno točko A. Še slika hamiltonovega cikla:
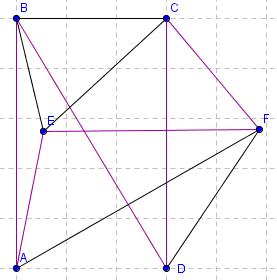
Hamiltonov cikel - vaje
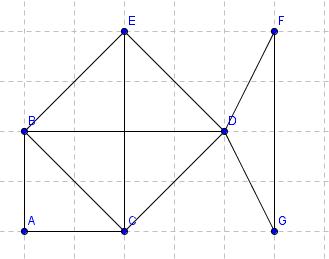
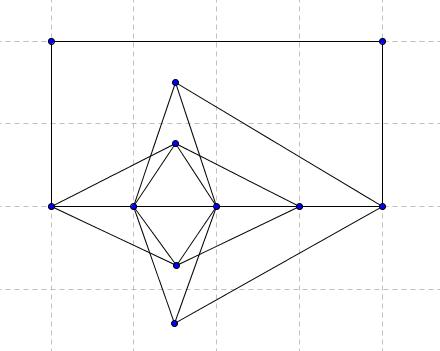
4. naloga Poglejmo si še en primer. Dan je graf:
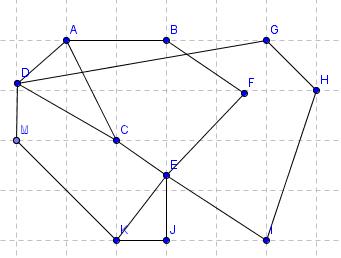
Spomnimo se na trditev iz teorije. Ena trditev pravi, da če grafu odstranimo k točk in graf, ki ostane, razpade na več kot k delov, potem ta graf ni hamiltonov. Pa naredimo to na danem grafu. Odstranimo točki D in E, ki imata največjo stopnjo. Odstranili smo 2 točki, dobili pa smo graf, ki je trodelen. Torej po trditvi ta graf ni hamiltonov. Še slika:
Hamiltonov cikel - vaje
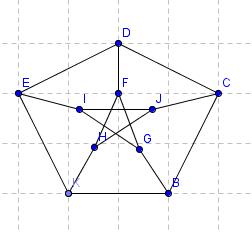
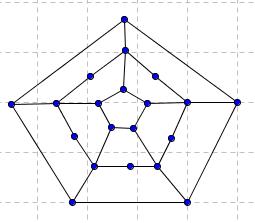
Hamiltonov cikel - vaje
Pri reševanju nalog v prosojnicah hamilton - vaje, vam bo prav prišla kratka animacija, ki vam pomaga poiskati hamiltonov cikel: