Kralja so vprašali po sinovi starosti. Kralj, ki je nadvse ljubil matematiko, je sinovo starost zavil v matematično uganko. Poslušaj jo in poskusi zapisati besedilo z matematičnimi znaki.
Kakšno enačbo dobimo?
Besedilne naloge I
Besedilne naloge I
E-um (vsebinsko), Skupina NAUK (tehnično)
Kraljevičeva leta
Odlično, rešitev je pravilna.
To pa en bo držalo.
Če označimo kraljevo starost z , kraljičino z , sinovo pa z , se iskana enačba glasi:
Kraljevičeva leta
V dobljeni enačbi nastopajo algebrajski ulomki. Pri reševanju takšnih enačb smo se najprej vprašali, kdaj je naloga sploh smiselna. Enačba in tudi zdrava pamet pravita, da kralj in kraljica ne smeta biti stara let. Še vedno ne vemo, koliko je star sin.
Iz enačbe izrazi sinovo starost.
Nam je kralj v resnici razkril sinovo starost?
Kaj bi nam moral kralj še povedati, da bi lahko izračunali sinovo starost?
Kralj tudi svoje in kraljičine starosti ni povedal brez ovinkov. Poslušaj, kaj je dodal.
Poskusi sedaj izračunati sinovo starost.
Enačbo moramo preoblikovati tako, da izrazimo neznanko . Ker kraljičina in kraljeva starost nista , smemo enačbo pomnožiti z .
Na levi izpostavimo in delimo z .
Ne. Izvedeli smo samo, kakšna je zveza med sinovo starostjo ter starosto kralja in kraljice.
Kralj bi nam moral povedati še svojo in kraljičino starost.
V prej zapisanem izrazu za upoštevamo, da je .
Kraljev sin je star pol leta. Koliko sta stara kralj in kraljica, pa še vedno ne vemo.
Je reklama goljufiva?
Trgovec Maks ima v izložbi napis: „Pri nas prodajamo meter blaga po ceni €, vendar vam pri nakupu metre blaga podarimo”. Trgovec Srečko na drugi strani ulice pa se hvali: „Pri nas vam prodamo meter blaga po €, vendar vaš račun zmanjšamo za €”. Sosedi Mara in Ana sta kupili blago vsaka pri enem od omenjenih trgovcev. Ko sta se srečali, sta ugotovili, da sta ne glede na različni ponudbi na koncu obe dobili enako količino blaga in tudi zneska, ki sta ju odšteli, sta bila enaka. Koliko metrov blaga je kupila vsaka od sosed?
Količino kupljenega blaga označimo z . Soseda, ki je kupila blago pri trgovcu Maksu, je zanj odštela , račun druge sosede pa je znašal . Če sta plačali enako, velja enakost
Odpravimo oklepaje in člene z neznanko prenesemo na levo, ostale na desno stran enačaja.
Izpostavimo neznanko:
Če je , je katero koli realno število, saj dobimo
Če ni , pa smemo enačbo deliti z in dobimo
Ta rešitev ni smiselna, saj cena ne more biti negativna, količina kupljenega blaga pa tudi ne. Ostane nam le možnost, da je . V tem primeru pa ne moremo ugotoviti, koliko metrov blaga sta sosedi kupili.
Kako tlakovati?
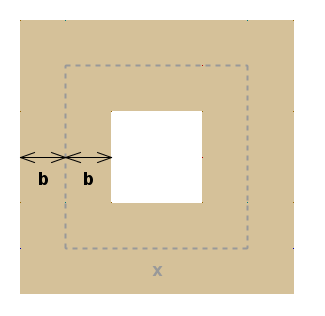
Peter bo na vrtu postavil mizo kvadratne oblike. Prostor okoli mize bo tlakoval z rečnimi kamni. Peter lahko s kamni tlakuje m površine. Želi si tlakovati področje v obliki kvadratnega kolobarja, ki bi segalo metrov od vsake strani mize in metrov pod mizo. Poiščimo zvezo med velikostjo mize in širino kvadratnega kolobarja.
|
Na skici tlakovanega področja je tloris mize vrisan črtkano. Stranico mize označimo z . Notranji kvadrat, ki omejuje tlakovano področje, ima stranico (stranico mize na vsaki strani zmanjšamo za ), zunanji pa (stranico mize na vsaki strani povečamo za ). Ploščina tlakovanega področja je enaka razliki ploščin zunanjega in notranjega kvadrata in meri m.
Oklepaja na levi strani odpravimo in enačbo preuredimo:
Našli smo zvezo med stranico mize in . Stranica mize meri . Pri smiselnih podatkih ( ni ), je tudi rešitev smiselna.
Zaslužek
Trgovec je kupil izdelek po nabavni ceni € in ga prodal za €, pri tem pa je zaslužil odstotkov nabavne cene izdelka. Izračunaj nabavno ceno izdelka.
Nabavna cena izdelka je:
Odlično, rešitev je pravilna.
To pa en bo držalo.
Spomnimo se, kako neko osnovo povečamo za odstotkov:
Upoštevajmo, da smo za odstotkov povečali osnovo in da je povečana vrednost :
Obe strani enačbe pomnožimo s in vse člene prenesemo na levo:
Dobili smo enačbo višje stopnje, ki jo rešimo z razcepom na faktorje, katerih produkt je . Uporabimo Vietovo pravilo:
Eden od obeh faktorjev mora biti , torej , kar da , ali pa , kar da .
Prva, negativna rešitev je nesmiselna, saj cena ne more biti negativna.
Nabavna cena izdelka je torej €.
Zapletena leta
Na srečanju šestdesetletnikov se srečata stari znanki Meta in Tina. Ker se že zelo dolgo nista videli, si imata veliko povedati. Druga drugi predstavita tudi svoji družini. Meta je navdušena ugankarica in takole predstavi starost svojega sina.
Koliko je star Metin sin?
Metin sin je star
Preveri
Kaj bi lahko povedal o sinovi starosti, če ne bi vedel, koliko je stara Meta?
Odlično, rešitev je pravilna.
To pa en bo držalo.
Metine besede moramo zapisati z matematičnimi simboli. Da nam bo lažje, si še enkrat preberimo besedilo. Meta pravi: „Veš Tina, danes imam trikrat toliko let, kot jih je imel moj sin v času, ko sem bila jaz toliko stara, kot je moj sin danes.”
Označimo z sinovo starost. Ne vemo, za koliko let nazaj se nanaša Metin opis. Število preteklih let označimo z .
Meta ima danes let, kar je trikrat toliko, kot jih je imel sin pred leti. Tedaj je bil sin star let, kar je tretjina Metinih sedanjih let, torej .
Tedaj je bila Meta stara let, kar je toliko, kot je sin star danes, torej .
Ker nas zanima sinova starost, izrazimo iz zadnje enakosti :
in to upoštevamo v prvi enačbi.
od tod pa in .
Odgovor: Metin sin je star let.
Odlično, rešitev je pravilna.
To pa en bo držalo.
Metina leta označimo z , ostale spremenljivke pa enako kot v prvem delu naloge.
Meta je danes stara trikrat toliko, kot je bil sin pred leti:
Pred leti pa je bila stara toliko, kot je sin danes:
Zanima nas zveza med Metino in sinovo starostjo, zato z in izrazimo :
in to upoštevamo v prvi enačbi:
od tod pa dobimo
oziroma
Odgovor: Sin ima dve tretjini Metinih let.
Bazen
Bazen polnimo iz dveh cevi. Če bi bazen polnili le iz prve cevi, bi bil poln v dveh urah, če pa bi ga polnili le iz druge cevi, bi za polnjenje porabili tri ure. Bazen ima dva odtoka enake zmogljivosti. Ko smo polnili bazen iz obeh cevi, smo pozabili zapreti odtoka. Po šestih urah polnjenja se je bazen napolnil z vodo.
V kolikšnem času se bazen izprazni skozi oba odtoka, če zapremo oba dovoda vode?
V kolikšnem času pa se bazen izprazni skozi enega od odtokov?
Odlično, rešitev je pravilna.
To pa en bo držalo.
Z označimo čas, v katerem se bazen izprazni skozi en odtok. V eni uri se bazen iz prve cevi napolni do polovice, iz druge pa do tretjine volumna celotnega bazena. Skupaj priteče v eni uri v bazen za celotnega volumna vode. V eni uri izteče skozi en odtok celotnega volumna bazena, skozi dva odtoka pa . Stanje vode v bazenu po eni uri je celotnega volumna, po šestih urah pa šestkrat toliko in takrat je bazen poln. Torej .
Iz zadnje enačbe izrazimo :
Od tod pa .
Odgovor: Bazen se izpazni skozi en odtok v treh urah, skozi oba pa v eni uri in pol.
1. naloga
Pred petimi leti je bila Neža tretjino mlajša od Nike, čez pet let pa bo Nika tretjino starejša od Neže. Izračunaj, koliko sta Neža in Nika stari danes.
Odlično, rešitev je pravilna.
To pa en bo držalo.
Označimo Nežino današnjo starost z , Nikino pa z . Pred petimi leti je bila Neža stara , Nika pa . Torej velja:
Čez pet let bo Neža stara , Nika pa . Torej velja:
Iz prve enačbe izrazimo :
Dobljeni izraz vstavimo v drugo enačbo:
Enačbo preuredimo in od tod dobimo in ter .
Odgovor: Neža je stara , Nika pa let.
2. naloga
Spremenimo prvo nalogo. Pred leti je bila Neža tretjino mlajša od Nike, čez let pa bo Nika tretjino starejša od Neže. Izračunaj, koliko sta Neža in Nika stari danes.
Odlično, rešitev je pravilna.
To pa en bo držalo.
Označimo Nežino današnjo starost z , Nikino pa z . Pred leti je bila Neža stara , Nika pa . Torej velja:
Čez let bo Neža stara , Nika pa . Torej velja:
Iz prve enačbe izrazimo :
Dobljeni izraz vstavimo v drugo enačbo:
Enačbo preuredimo
in od tod dobimo
in ter .
Odgovor: Neža je stara , Nika pa let.
3. naloga
Nek mož je šel v tuj sadovnjak in nabral pomaranče. Pot iz sadovnjaka je vodila
skozi tri zastražena vrata, a mož je podkupil stražarje. Prvemu stražarju je dal polovico vseh nabranih pomaranč in še dve povrhu, drugemu je dal polovico preostalih pomaranč in še dve povrhu, tretjemu spet polovico preostalih pomaranč in še dve povrhu. Ven je prišel z eno samo pomarančo. Koliko pomaranč je mož nabral v sadovnjaku?
(Nalogo je sestavil Abraham ben Meir ibn Ezra, rojen v Španiji leta 1092.)
Mož je v sadovnjaku nabral
Odlično, rešitev je pravilna.
To pa en bo držalo.
Označimo z število nabranih pomaranč. Ko je dal pomaranče prvemu stražarju, sta mu ostali dve manj kot polovica, torej . Ko je dal pomaranče drugemu, sta mu spet ostali dve pomaranči manj od polovice prejšnjega izraza, torej
Spet podobno, ko je podkupil tretjega
Sedaj mu je ostala le še ena pomaranča
Odgovor:: Če rešimo zadnjo enačbo, ugotovimo, da je mož nabral pomaranč.
Rezultati
