Trikotnik in krožnica
Trikotniku očrtana krožnica
Super, rešitev je pravilna.
To pa ne bo držalo.
Simetrala daljice je množica vseh tistih točk, ki so enako oddaljene od obeh krajišč daljice.
Iščemo točke, ki so enako oddaljene od krajišč daljice .
Trikotniku očrtana krožnica
Pojdimo še korak naprej in poiščimo vse tiste točke, ki so enako oddaljene od oglišč in . Seveda je to še ena simetrala.
A sedaj že veš, kje bi lahko bilo središče trikotniku očrtane krožnice?
Trikotniku očrtana krožnica
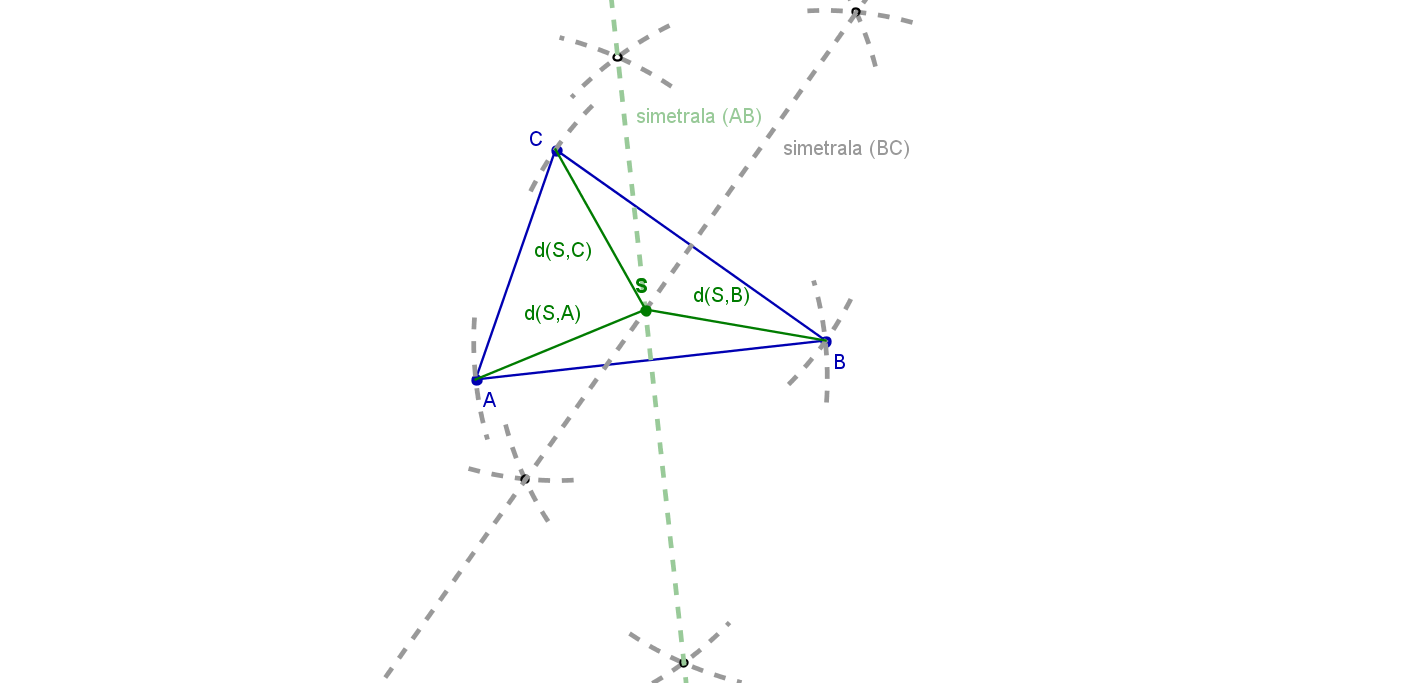
Presečišče obeh simetral označimo s . Ker je na simetrali daljice , velja, da je . Ker pa ta točka leži tudi na simetrali daljice , velja tudi, da je .
Sedaj pa poglejmo oba matematična zapisa in se spomnimo neke zelo lepe lastnosti razdalje, ki ji pravimo tranzitivnost. (Saj veš, to je tista lastnost, ki pravi, da če je ena razdalja enaka drugi in je ta druga razdalja enaka tretji, potem je jasno, da je tudi prva razdalja enaka tretji.)
Torej pri nas velja: . In prav to smo želeli. Našli smo torej točko, ki je enako oddaljena od vseh treh oglišč.
Konstrukcija trikotniku očrtane krožnice
Spodnji aplet ti omogoča, da konstrukciji slediš po korakih. Pod konstrukcijo so v levem vogalu smerne oznake. Prva te postavi na začetek konstrukcije, druga te vodi po korakih naprej, tretja pa ti pokaže končno sliko.
1. Narišemo simetralo daljice .
2. Narišemo simetralo daljice .
3. Točka, kjer se simetrali sekata, je središče trikotniku očrtane krožnice.
4. Polmer krožnice pa je razdalja od točke do katerega koli oglišča.
Konstrukcija trikotniku očrtane krožnice
Z miško primi in premikaj oglišča narisanega trikotnika. Opazuj, kdaj leži središče trikotniku očrtane krožnice v trikotniku, kdaj leži na stranici in kdaj leži zunaj trikotnika.
Dopolni spodnje povedi.
Središče očrtane krožnice je znotraj trikotnika, če je trikotnik koten, zunaj njega pa tedaj, ko je trikotnik koten.
Središče očrtane krožnice leži na stranici, ko je trikotnik koten.
Super, rešitev je pravilna.
To pa ne bo držalo.
Središče ostrokotnemu trikotniku (to so tisti trikotniki, ki imajo vse notranje kote manjše od ) očrtane krožnice je v notranjosti trikotnika.
Središče topokotnemu trikotniku (topokotni so tisti trikotniki, ki imajo en notranji kot večji od ) očrtane krožnice je zunaj trikotnika.
Središče pravokotnemu trikotniku očrtane krožnice leži natanko na sredini hipotenuze.
Razmisli 1
Super, rešitev je pravilna.
To pa ne bo držalo. Kje pa bi še lahko ležalo?
Pravilno. Središče trikotniku očrtane krožnice je v notranjosti trikotnika le, če je trikotnik ostrokoten.
Do enakega spoznanja smo prišli tudi pri višinski točki (ortocentru).
Narobe. Središče trikotniku očrtane krožnice je v notranjosti trikotnika le, če je trikotnik ostrokoten.
Do enakega spoznanja smo prišli tudi pri višinski točki (ortocentru).
Super, rešitev je pravilna.
Narobe.
Središče pravokotnemu trikotniku očrtane krožnice je na sredini hipotenuze, saj je ta točka enako oddaljena od vseh treh oglišč.
Trikotniku ABC očrtaj krožnico
Na voljo imaš nekaj preprostih geometrijskih orodij, s katerimi moraš konstruirati trikotniku očrtano krožnico.
Ko bo naloga pravilno opravljena, se ti bo izpisalo Narejeno.
Trikotniku včrtana krožnica
Sedaj pa je pred nami malce trši oreh. Želimo namreč ugotoviti, kje leži središče trikotniku včrtane krožnice.
Krožnica, ki je včrtana trikotniku, se od znotraj dotika vseh njegovih stranic. Nosilke stranic trikotnika so torej tangente včrtanega kroga. V točki , kjer se krožnica dotakne stranice, je polmer včrtane krožnice pravokoten na stranico. Torej je središče včrtane krožnice točka, ki je enako (za polmer trikotniku včrtanega kroga) oddaljena od vseh treh stranic.
Razdalja med točko in premico je dolžina najkrajše daljice, ki točko povezuje s premico. To pa je vedno pravokotna razdalja med izbrano točko in dano premico.
Razmisli 2
Super, rešitev je pravilna.
Narobe.
Točke ležijo na simetrali kota med stranicama in .
Razmiljaš lahko po sledeči poti:
1. Izberemo eno "tako" točko in narišemo obe pravokotnici na dani premici. Med premicama in pravokotnicama nastane deltoid.
2. Ta postopek lahko ponovimo za več različnih točk in tako dobimo več različnih deltoidov, ki pa so si vsi med seboj podobni. Vsi podobni si liki pa imajo enako velike kote.
3. Presečišče danih premc in "taka" točka sta krajišči tiste deltoidove diaonale, ki deltoid razdeli na dva skladna trikotnik. Ta diagonala je torej simetrijska os deltoida in zatorej razpolvlja dva notranja kota deltoida.
4. Sedaj pa se je samo še potrebno spomnit, kako rečemo poltraku, ki razpolavlja kot.
Razmisli 2
Nadaljujmo z razmislekom o tem, kje ležijo tiste točke, ki so enako oddaljene od nosilk stranic in .
Po podobnem premisleku kot zgoraj bodo vse take točke ležale na simetrali kota med stranicama in .
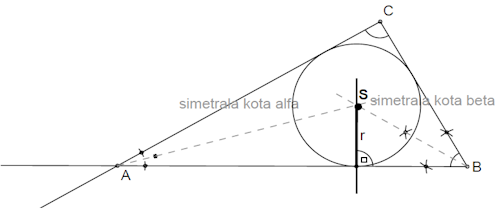
Konstrukcija trikotniku včrtane krožnice
S puščicami pod apletom lahko po korakih slediš poteku konstrukcije.
Potek konstrukcije:
1. Narišemo simetralo kota .
2. Narišemo simetralo kota .
3. Označimo presečišče narisanih simetral kot središče trikotniku včrtane krožnice.
4. Skozi tako konstruirano središče postavimo pravokotnico na eno od stranic in določimo velikost polmera včrtane krožnice.
Trikotniku ABC včrtaj krožnico
Nalogo reši s ponujenimi orodji.
Ne pozabi natančno določiti polmera včrtane krožnice. Če ne gre, znova poglej potek konstrukcije na zgornji predstavitvi.
Opomba: Če želiš risati krožnice z enako velikimi polmeri, uporabi orodje „krožnica s konstantnim polmerom”. Ko je orodje izbrano, najprej klikni na mesto, kjer mora biti postavljeno središče, nato pa kamor koli na risalno površino. Po drugem kliku se ti bo odprlo okno za urejanje krožnice in tu moraš v vrstici „Polmer” vedno določiti enako velikost polmera.
Eulerjeva premica
Nariši premico, ki poteka skozi težišče, in višinsko točko trikotnika.
Ko je naloga narejena, uporabi orodje za Premikanje objektov (puščica s piko) in premikaj oglišča trikotnika ter opazuj premico, ki si jo narisal.
Ali opaziš kaj zanimivega?
Razmisli 3
Na premici, ki poteka skozi težišče trikotnika in višinsko točko, vedno leži tudi
Super, rešitev je pravilna.
Narobe.
Središče očrtanega kroga.
1. naloga
Nariši trikotnik s stranicami cm, cm in cm ter mu očrtaj krožnico.
Konstrukcija trikotnika je zelo preprosta in ne potrebuje posebne razlage. Središče očrtane krožnice dobimo s simetralami stranic.
2. naloga
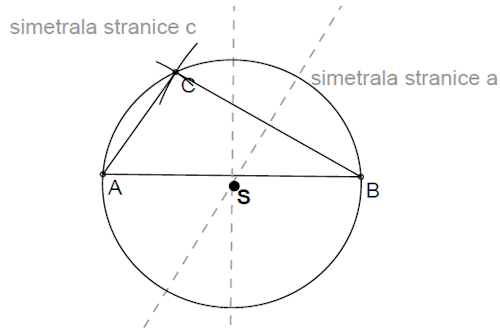
Nariši enakokraki trikotnik s krakom cm, katerega očrtana krožnica ima polmer cm.
Potek konstrukcije:
1. Narišemo krožnico s polmerom cm.
2. Izberemo poljubno nekje na krožnici oglišče , iz katerega bosta izhajala kraka trikotnika.
3. Narišemo krožnico s polmerom cm in središčem v točki . Presečišči danih krožnic sta oglišči in .
3. naloga
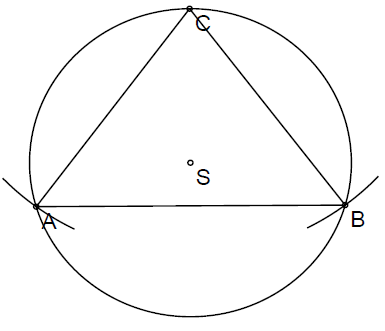
Nariši trikotnik s stranico cm in tej stranici priležnima kotoma in . Danemu trikotniku včrtaj krog.
Konstrukcija trikotnika je zelo preprosta in ne potrebuje posebne razlage. Središče včrtanega kroga dobimo s simetralami kotov.
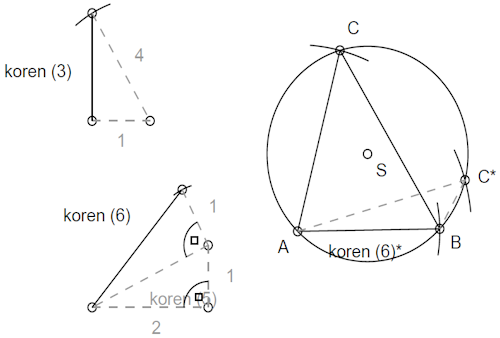
4. naloga
Konstruiraj trikotnik s stranicama cm in cm ter polmerom trikotniku očrtanega kroga cm.
Najprej je treba posebej konstruirati daljici dolžine cm in cm.
Konstrukcija trikotnika poteka podobno kot pri 2. nalogi. Vendar pazi, saj lahko z danimi podatki konstruiramo dva različna (neskladna) trikotnika.
Rezultati
- Trikotniku očrtana krožnica
- Konstrukcija trikotniku očrtane krožnice
- Razmisli 1
- Trikotniku ABC očrtaj krožnico
- Trikotniku včrtana krožnica
- Razmisli 2
- Konstrukcija trikotniku včrtane krožnice
- Trikotniku ABC včrtaj krožnico
- Eulerjeva premica
- Razmisli 3
- 1. naloga
- 2. naloga
- 3. naloga
- 4. naloga
- Rezultati