Ob spodnji sliki lahko ponoviš najpomembnejša spoznanja o povezavi med obodnimi in središčnimi koti.
1. Vsi obodni koti nad danim lokom so enako veliki.
2. Središčni kot nad danim lokom je dvakrat večji od pripadajočega obodnega kota.
Talesov izrek
Talesov izrek
E-um (vsebinsko), Skupina NAUK (tehnično)
Talesov izrek o kotih v polkrogu
Talesov izrek o kotih v polkrogu
Na spodnji sliki premikaj vrh obodnega kota, ki je narisan nad premerom danega kroga in opazuj, kako se spreminja njegova velikost. Kaj ugotoviš?
Premikaš lahko tudi krajišči premera in s tem večaš oziroma manjšaš polmer kroga.
Poskusi.
Na sliki vidimo, da meri kot , ne glede na to, kako premikamo oglišča.
Dokaz
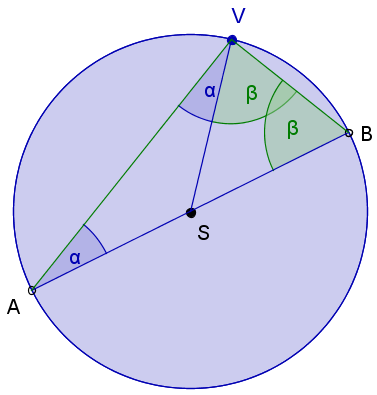
| Trikotnika in sta enakokraka. Vsota notranjih kotov obeh trikotnikov je . V trikotniku imamo dva kota in kot . V trikotniku pa dva kota in kot . Vemo tudi, da sta kota in sokota in skupaj merita . Za vsoto notranjih kotov obeh trikotnikov torej velja: . Upoštevamo, da sta kota in suplementarna in je njuna vsota enaka , pa pridemo do enačbe . Na obeh straneh enačbe odštejemo in dobimo . Sedaj moramo enačbo samo še deliti z in že imamo dokazano, da je . |
Zgoraj zapisano ugotoivtev je poznal že starogrški matematik Tales iz Mileta, zato ji pravimo TALESOV IZREK. Talesov izrek je uporaben pri mnogih konstrukcijah.
Tales iz Mileta (od 624 do 546 pr.n.št.)
Slika je v javni lasti na naslovu: http://sl.wikipedia.org/wiki/Tales
Tales velja za ustanovitelja grške znanosti, matematike in filozofije. Veliko je potoval po Egiptu in Mezopotamiji in na svojih potovanjih zbral veliko znanja. Žal pa ni ohranjeno nobeno njegovo napisano delo in zato težko potrdimo kaj od tega kar mu pripisujemo je tudi resnično njegovo.
Najbolj slaven je postal po napovedi sončnega mrka, ki se je zgodil prav v napovedanem letu 585 pr.n.št.
Za matematike pa je vsekakor najpomembnejše njegovo prepričanje, da ni dovolj če pojave le opazujemo pač pa jih je potrebno tudi dokazovat. Tales je prvi, ki je poskusil svoja stališča pojasnit z logičnim razmišljanjem in ne z nadnaravnimi pojavi.
Mnoge knjige o zgodovini matematike pripisujejo Talesu kar precej geometrijskih trditev:
- Premer deli krog na dva enaka dela.
- Kota ob osnovnici enakokrakega trikotnika sta skladna.
- (Sovršna) kota med sekajočima premicama sta skladna.
- Dva trikotnika sta skladna, če imata enako velika dva kota in eno stranico.
- Koti na polkrožnici so pravi koti.
Obstaja pa tudi nekaj zapisov o tem, kako je Tales izračunal višino piramide. Počakal je na trenutek, ko so bile sence predmetov enako dolge kot njihove dejanske velikosti. To je uporabil pri piramidi, katere višino je s pomočjo sence (v pravem trenutku) lahko določil.
Iznašel naj bi tudi metodo za izračun oddaljenosti ladje od brega.
Platon pa v svojih zgodbah omenja anekdoto o tem, kako je neke noči Tales pešačil proti domu in pri tem proučeval zvezdno nebo. Kar ni pazil kje stopa, je padel v jarek. Lepa mlada služkinja, ki mu je pomagala izvleči se iz jarka pa mu je rekla: "Le kako lahko pričakuješ, da boš razumel kaj se dogaja na nebu, če ne vidiš niti tega, kar je pred tvojimi nogami."
To je verjetno prva v zgodovini zapisana šala na račun raztresenih profesorjev.
Konstrukcija 1
Konstrukcija tangente na dano krožnico, skozi dano točko , ki leži na dani krožnici.
Konstrukcija 2
Konstrukcija tangente na dano krožnico, skozi dano točko , ki ne leži na dani krožnici.
Naloga 1
Konstruiraj obe tangenti na dano krožnico skozi dano točko .
Uporaba Talesovega izreka pri konstrukciji trikotnika
Konstruiraj trikotnik s podatki:
cm
cm
cm
Konstruirajmo pravokotni trikotnik
Spodaj se lahko sprehodiš skozi konstrukcijo pravokotnega trikotnika s podatkoma za hipotenuzo cm in težiščnico na kateto cm.
Pomoč
Za pomoč k prejšnji nalogi:
Dana je krožnica in njena tetiva - daljica . Razpolovišča tetiv, ki imajo eno krajišče v točki , drugo pa kjerkoli na krožnici se nahajajo na krožnici s premerom .
Nalogo bi lahko rešili tudi s pomočjo paralelograma.
Naredi sam
Konstruiraj pravokotni trikotnik, katerega hipotenuza meri cm, višina nanjo pa cm.
Naloga ima dve rešitvi. Tvoja naloga bo končana, ko boš oba pravokotna trikotnika izrisal kot mnogokotnika.
Konstruiraj enakokrak trikotnik
Konstruiraj enakokrak trikotnik, v katerem meri osnovnica cm, višina na krak pa cm.
Naloga bo končana, ko boš določil točko .
Rešitev podobnega primera
Na spodnji animaciji je opisan potek konstrukcije enakokrakega trikotnika z osnovnico dolgo cm, višino na krak pa cm.
Ponovimo
Super, rešitev je pravilna.
To pa ne bo držalo.
Vsi obodni koti v polkrogu so pravi koti.
Super, rešitev je pravilna.
To pa ne bo držalo.
Velikost obodnega kota na polkrožnici ni odvisna od velikosti polmera dane krožnice.
Super, rešitev je pravilna.
Ponovimo
Super, rešitev je pravilna.
To pa ne bo držalo.
Na sredini hipotenuze.
Super, rešitev je pravilna.
To pa ne bo držalo.
Skladnost kotov ob osnovnici enakokrakega trikotnika, suplementarnost sokotov, in vsoto notranjih kotov v trikotniku, ki je enaka .
1. naloga
Pri vsakem spodaj navedenem vprašanju nariši najprej krožnico s polmerom cm.
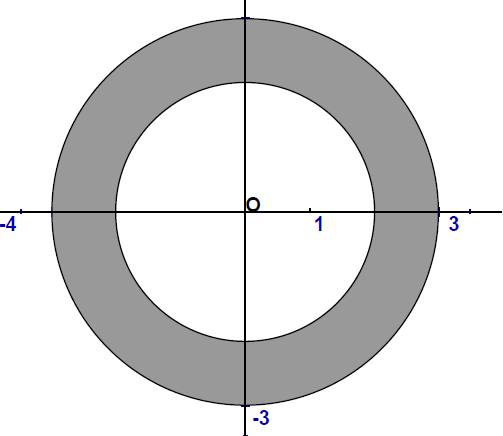
a) Nariši množico točk, ki so od središča oddaljene vsaj cm in ne več kot cm.
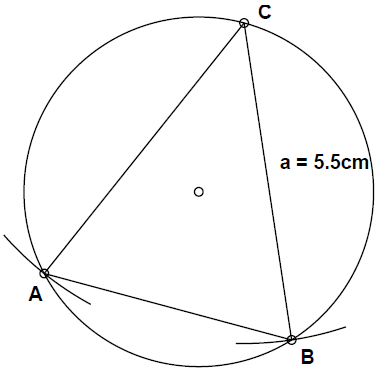
b) Nariši enakokrak trikotnik s krakom cm, ki mu je dana krožnica očrtana.
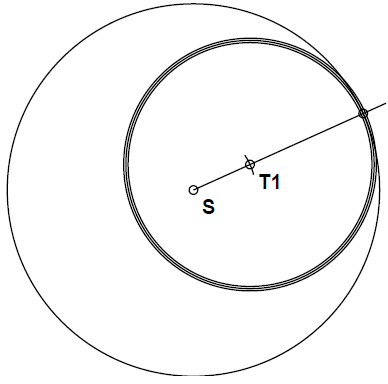
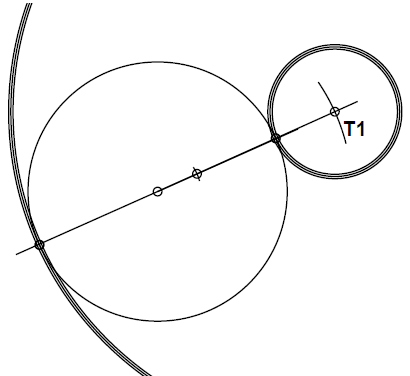
c) Nariši točko , ki je od središča oddaljena cm. Nariši krožnico, ki ima središče v in se dane krožnice dotika.
d) Nariši točko , ki je od središča oddaljena cm. Nariši vse krožnice, ki imajo središče v in se dane krožnice dotikajo. Kolikšni so polmeri teh krožnic?
e) Izberi točko v zunanjosti kroga in konstruiraj tangento na dano krožnico, ki gre skozi dano točko .
Rešitev je na sliki vidna kot siv kolobar.
Izberemo vrh kota med krakoma. Narišemo lok, ki ima vrh v izbranem oglišču in polmer enak dolžini kraka. Kjer lok seče krožnico sta točki in .
Narisana krožnica ima polmer cm.
Krožnici imata polmera velika cm in cm.
Potek je opisan v gradivu.
2. naloga
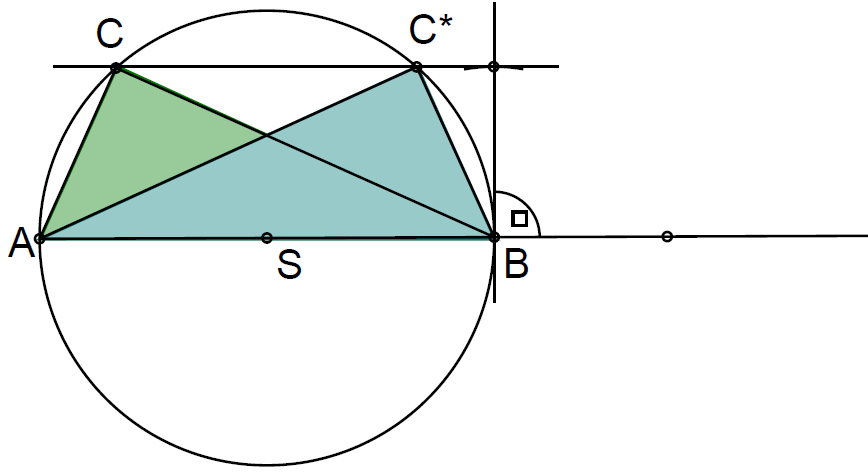
Konstruiraj pravokotni trikotnik, če meri polmer temu trikotniku očrtane krožnice cm, višina na hipotenuzo pa cm.
1. Narišemo krožnico s polmerom cm.
2. Enega od premerov izberemo za hipotenuzo .
3. Narisanemu premeru postavimo cm oddaljeno vzporednico.
4. Oglišče je tam kjer se vzporednica in krožnica sekata. Naloga ima dve rešitvi.
3. naloga
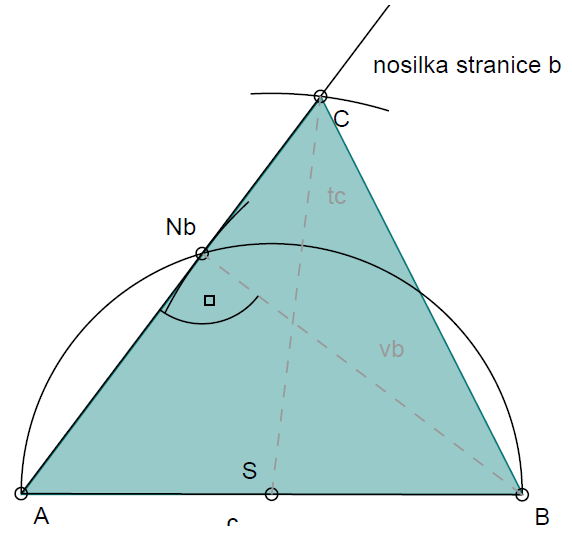
Konstruiraj trikotnik, v katerem meri stranica cm, višina cm, težiščnica cm.
1. Narišemo stranco .
2. S pomočjo obodnih kotov v polkrogu in dane višine določimo njeno nožišče na stranico , to je točka .
3. Narišemo nosilko stranice .
4. Določimo središče stranice in s pomočjo dane težiščnice in nosilke stranice pridemo do oglišča .
4. naloga
Konstruiraj enakokrak trikotnik, katerega osnovnica meri cm, višina na krak pa cm.
Postopek je opisan v gradivu.
Rezultati
- Talesov izrek o kotih v polkrogu
- Dokaz
- Tales iz Mileta (od 624 do 546 pr.n.št.)
- Konstrukcija 1
- Konstrukcija 2
- Naloga 1
- Uporaba Talesovega izreka pri konstrukciji trikotnika
- Konstruirajmo pravokotni trikotnik
- Pomoč
- Naredi sam
- Konstruiraj enakokrak trikotnik
- Rešitev podobnega primera
- Ponovimo
- 1. naloga
- 2. naloga
- 3. naloga
- 4. naloga
- Rezultati
