Transformacija v ravnini, ki vsako razdaljo pomnoži z realnim številom, se imenuje središčni razteg. Točka, ki pri tej preslikavi ostaja na svojem mestu, se imenuje središče raztega. Tak razteg preslika trikotnik v podobni trikotnik, kot lahko vidimo na naslednji animirani sliki.

Računalniku prepustimo merjenje dolžin stranic in računanje razmerij. Na sliki enostavno spremljamo rezultate pri spreminjanju dolžin podaljšanih stranic, ko pomikamo rdečo točko na drsniku zgoraj.

Za dokaz tega izreka je dovolj, da skozi načrtamo vzporednico daljici in nato po Talesovem izreku ugotovimo, da točka leži na presečišču te vzporednice s poltrakom .

Podoben izrek poznamo tudi pri skladnih trikotnikih, omogoči pa nam hitreje priti do podobnih trikotnikov. Primer uporabe pa lahko vidimo na naslednji sliki.

Pajek in muha se odpravita z enakima hitrostma vsak v svojo smer. Potem je njuna zveznica vedno pod istim kotom, glede na smer poti enega in drugega. Razdalja med njima pa se veča z enako hitrostjo, kot jo imata pajek in muha.

Vemo že, da so stranice v enakem razmerju, če sta trikotnika podobna. Pa velja tudi obratno? Velja, zato lahko povemo še en izrek:

Srednjica trikotnika je primer pomembnega dejstva, ki ga lahko tudi dokažemo s pomočjo podobnosti. Trdimo namreč, da je zveznica razpolovišč dveh stranic v trikotniku enaka polovici dolžine treje stranice in ji je vzporedna.

Srednjica trikotnika je zveznica razpolovišč dveh stranic v trikotniku. Imenujmo ti razpolovišči in . Povezuje pa naj razpolovišči stranic in . Tedaj dobimo dva trikotnika in . V teh trikotnikih imamo skladen en kot, kot pri , ali kot , stranici in trikotnika pa sta s faktorjem povečani stranici in trikotnika . Po prvem izreku o podobnosti trikotnikov sta torej trikotnika in podobna. Zato je srednjica enaka polovici stranice in ji je vzporedna.

Talesu iz Mileta pripisujejo merjenje višine piramide, zato najbrž tudi izreke poimenujemo po njem, čeorav je podobnih zgodb še več. Ne glede na to kdo in kako je to naredil, metoda je prav uporabna za merjenje višine predmeta, hriba, zgradbe, ki je previsoka, da bi jo izmerili kako drugače. Poglejmo najprej na sliko:

Od opazovališča je do točke m, v točki pa je m visoka palica, ki se s smerjo pokriva z vrhom piramide, ta pa je od oddaljena m. Tedaj je višina piramide:

V lepem sončnem dnevu bi podoben računa lahko naredili, da bi izmerili dolžino sence piramide in dolžino sence palice, potem pa po enakem računu kot zgoraj izračunali višino piramide.

Oboje pa temelji na podobnosti trikotnikov.

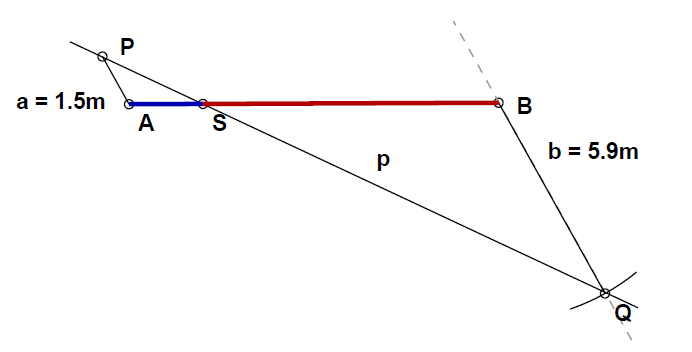
Razdeli daljico cm v danem razmerju, najprej na dela, ki sta enako dolga.

Daljici z dolžino cm narišemo na krajiščih na vzporednicah daljici enake dolžine v nasprotnih polravninah njene nosilke. Tako dobimo točki in . Če ti točki zvežemo, ta zveznica seka daljico točno na sredini. Predstavimo si to na sliki, saj slika pove več, kot tisoč besed.

Iz rezultatov in podatkov na sliki razberi, v kakšnem razmerju tokrat deli premica daljico .

Če si ugotovil, da je razmerje , je to zares razveseljivo, saj že dobro razumeš podobnost.

O podobnosti v naravi smo že veliko govorili. Pokažimo na primeru pridnega pajka, ki sicer svojo mrežo plete v zlobne namene, da vanjo zaplete svoj plen in vendar je njegova mreža ena najčudovitejših stvari, ki jih najdemo v naravi, ne glede na to, da je ponekod tudi zelo nadležna.

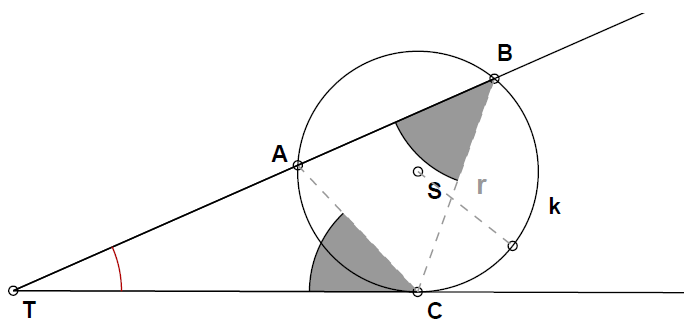
Poišči zvezo med podobnostjo in potenco točke glede na krog.

Iz podobnosti trikotnikov in lahko zapišemo:

od koder sklepamo naprej z besedami produkt odsekov, ki ju tvori poltrak iz zunanje točke in je enak kvadratu tangentnega odseka iz te točke .

Izrek o podobnosti s srednjico nas pripelje do pojma samopodobnosti in tako dobimo trikotnik Sierpinskega, ki predstavlja zanimiv uvod v fraktalno geometrijo. Ta trikotnik dobimo z zaporednimi ponavljanji včrtovanja trikotnika v enakostranični trikotnik, kjer v naslednji ponovitvi na enak način kot prej včrtamo trikotnik v vse tri trikotnike, razen sredinskega, kot vidimo na spodnji animaciji.

Še en primer podobnosti, kjer pa lahko še s preslikavo podobnost dodatno potrdimo. Seveda moramo razumeti, zakaj sta trikotnika podobna. V tem primeru gre za skladnost dveh kotov, kar pogojuje podobnost trikotnikov in .

Hincejeva sekvoja v Orešju pri Ptuju je zelo visoka. Da bi zmeril njeno višino, moraš uporabiti podoben trik, kot ga je uporabil Tales. Opiši postopek za primer sekvoje.

Izbereš lep sončen dan za sprehod do Orešja. Vzameš palico znane dolžine in izmeriš dolžino njene sence. Ker sekvoja ima svojo senco, lahko izmeriš tudi to. Označimo s višino sekvoje, s dolžino palice, s dolžino sence sekvoje in s dolžino sence palice. Naj ti izdam mere, pa boš brž lahko izračunal višino tega znamenitega drevesa. Imeli smo palico dolžine m, njena senca je bila dolga m; sekvoja pa je dajala senco z dolžino približno m. Sedaj pa iz podobnosti sledi .

Sekvoja je visoka približno m.

Trikotnik ima stranici cm in cm, kot . Ali je trikotnik z istim kotom in stranicama cm in cm podoben trikotniku ? Odgovor utemelji.

Preveri

Pajek in muha sta iz točk in krenila vsak po svoji poti vsak s svojo hitrostjo cm/s in cm/s, kot kaže slika. Razdalja od izhodišča do je cm, do pa cm. Kot med smerema je . Koliko sta med seboj oddaljena čez s?

Čez s sta med seboj oddaljena

Preveri

Trikotniku je stranici včrtana vzporednica , kot kaže slika. Izračunaj dolžini stranic in .

Preveri

V kakšnem razmerju deli daljica daljico m, če je dolžina daljice m, daljica pa meri m?

Preveri

Izračunaj dolžino tetive v krožnici , če so dane dolžine tangentnega odseka cm in daljice cm.

Preveri

Koliko meri polmer krožnice , če meri kot ?

Polmer krožnice meri:

Preveri

V trikotniku , v katerem sta in razpolovišči stranic in , meri srednjica cm. Koliko meri težiščnica , če je stranica dolga cm, kot ?

Preveri

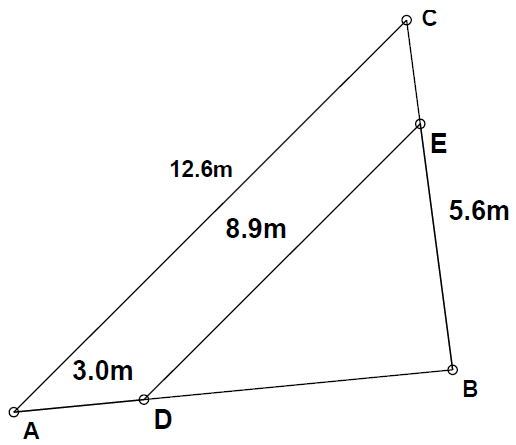
Izračunaj ploščino trikotnika, ki ga dobimo, če podaljšamo nevzporedni stranici trapeza, ki je podan s stranicami cm, cm, cm in cm. (glej sliko)

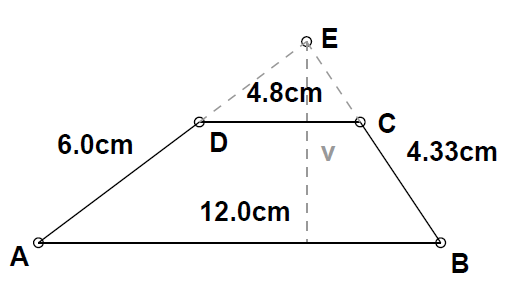
Ploščina trikotnika je:

Preveri