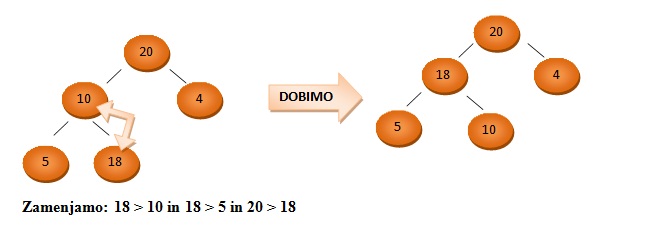
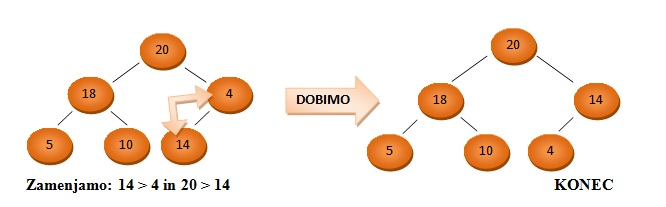
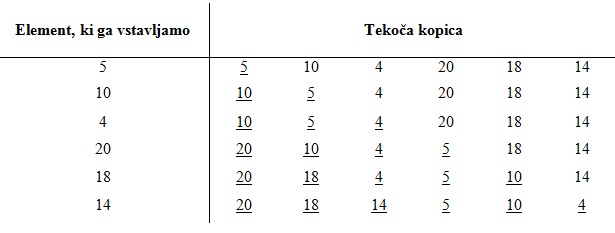
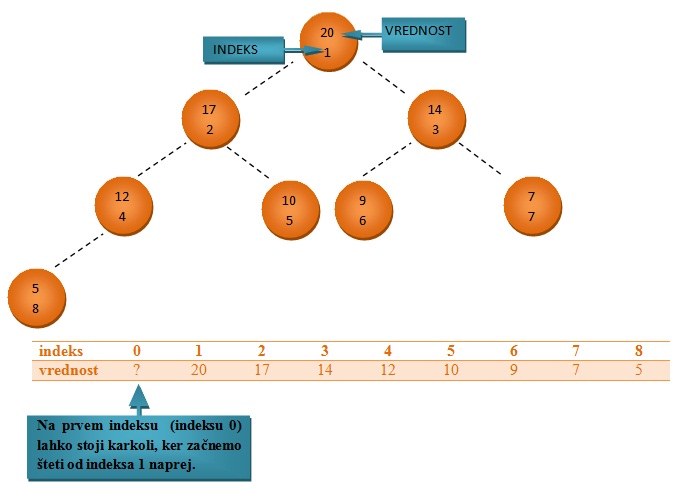
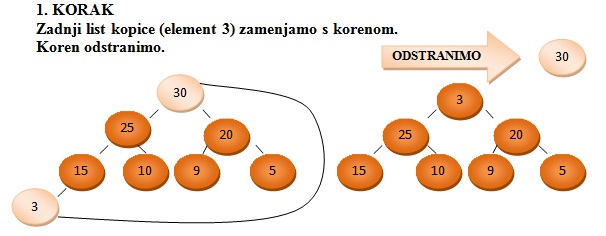
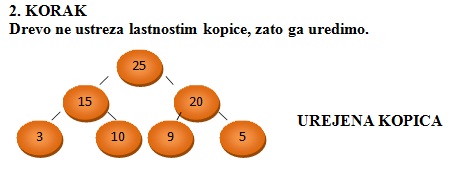
Kopico uvrščamo med levo poravnane in hkrati urejene drevesne podatkovne strukture.
Urejenost se nanaša na vozlišča, saj le ta vsebujejo elemente urejene po velikosti.
Levo poravnano drevo oziroma levo zapolnjeno drevo je drevo, v katerega elemente vstavljamo od leve proti desni ter hkrati ne moremo začeti zapolnjevati nekega sloja, če prejšnji sloj še ni zapolnjen.

Levo poravnano drevo

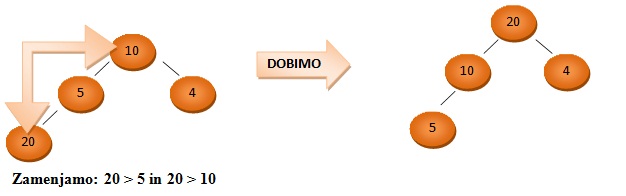
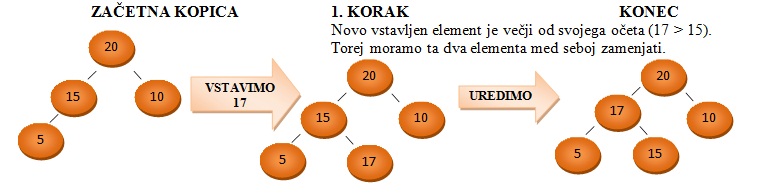
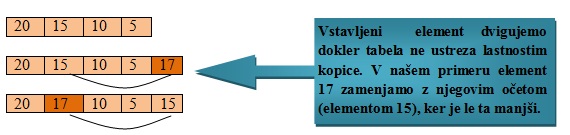
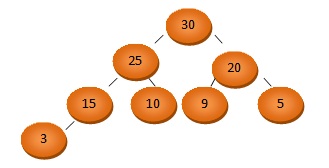
Glede na urejenost ločimo maksimalno in minimalno kopico.
Tudi levo poravnano drevo s samimi enakimi elementije kopica.

Maksimalna in minimalna kopica

• Višina kopice:
  

• Število listov:
  Primer:
  
  
  
  

  Kopica

• Element, ki ga hranimo v vozlišču očeta, ni manjši od elementa, ki ga hranimo pri sinovih:
  Podatek (starš) ≥ Podatek(otrok).
  
• Največji element se nahaja v korenu kopice.
  
• Poddrevesi maksimalne kopice sta prav tako predstavljata maksimalno kopico.
  

Maksimalna kopica

Minimalna kopica

• Element, ki ga hranimo v vozlišču očeta, ni večji od elementa, ki ga hranimo pri sinovih:
  Podatek(starš) ≤ Podatek(otrok).
  
• Najmanjši element se nahaja v korenu kopice.
  
• Poddrevesi minimalne kopice sta prav tako predstavljata minimalno kopico.
  

Minimalna kopica

Oblikovanje kopice

• Od narave problema je odvisno, kateri postopek bomo uporabili.
  
  
• Od tukaj naprej bo v vseh primerih uporabljena maksimalna kopica. Na podoben način naredimo vse tudi za minimalno kopico.
  

Osnovna operacija je vstavljanje novega element v tekočo, do sedaj zgrajeno kopico.

• Postopek:
  

  • element najprej vstavimo na n-to mesto (v list drevesa);
    
  • uredimo drevo tako da je na koncu nov element večji od svojih sinov in manjši od očeta;
    
  • to drevo je ponovno urejena kopica.
    

• PRIMER:
  Enega za drugim dobivamo naslednje elemente: 5, 10, 4, 20, 18, 14. Iz dobljenih elementov hočemo sestaviti (oblikovati) kopico z zaporednim vstavljanjem elementov v kopico.
  

1. Korak: Na začetku vzamemo prva dva elementa in tvorimo kopico.

• Potek vseh naslednjih korakov: Na vsakem koraku dodamo nov element in ga sproti preverjamo, da je urejen po pravilu kopice.
  

2. Korak

3. Korak

Primer obravnavamo na enakih podatkih kot prejšnjega in sicer vhodni elementi so 5, 10, 4, 20, 18, 14. Vsak korak bomo podčrtali element, ki je v tekočem koraku vstavljen v kopico.

Sestavljanje kopice v vektorju

• PREDNOST: Zaradi poznavanja elementov, ki jih želimo vstaviti, nam ni treba na vsakem koraku (ob vskame vstavljanju) pregledati podatkov, ki tvorijo trenutno kopico. Dovolj bo le, da kopico dobimo na koncu.
  

• Če želimo kopico predstaviti s pomočjo tabele, upoštevamo naslednja pravila:
  

  • Koren oz. oče je prvi element tabele (ničto mesto v tabeli zanemarimo).
    
  • Če je vozlišče na i-tem mestu, je njegov levi sin na mestu 2i, desni pa na mestu 2i+1.
    

  • Vozlišče na i-tem mestu ima torej svojega očeta na mestu i/2. Uporabimo celoštevilsko deljenje.
    

    Oblikovanje kopice iz tabele

• Poglejmo si element z indeksom 3, ki ima vrednost 14.
  

  • Levi sin: 2i = 2*3 = 6 (vrednost 9)
    
  • Desni sin: 2i+1 = 2*3+1 = 7 (vrednost 7)
    
  • Oče: i2 = 32 = 1 (vrednost 20)
    
    

• Poglejmo si element z indeksom 4, ki ima vrednost 12.
  

  • Levi sin: 2i = 2*4 = 8 (vrednost 5)
    
  • Desni sin: 2i+1 = 2*4+1 = 9 (ne obstaja)
    
  • Oče: i2 = 42 = 2 (vrednost 17)
    

Združi dve kopici in vozlišče tako, da znova dobimo kopico.

• Pogoj:
  

  • leva kopica mora biti polna,
    
  • desna kopica mora biti levo poravnana,
    
  • obe kopici morata imeti enako višino.
    

• Postopek:
  

  • tvori drevo z elementom x[i] kot korenom, ki ima poddrevesi drevesi s korenom 2*i+1 in 2*i+2
    

  • ponavljaj
    

    • če vrednost korena ne zadošča prvi lastnosti kopice, "premakni" vrednost korena v smeri večjega od otrok
      
    • premikanje zaključimo, če je izpolnjena prva lastnost kopice ali smo na zadnjem elementu v kopici
      

Imamo naslednjo tabelo:

Začetna tabela

Oranžno in rdečo obarvana polja predstavljajo poddrevesi, ki že ustrezajo lastnostim kopice (19 je večje od obeh otrok in sicer od 1 in od 13 ter 12 je večje od otroka 3).

Izpolnjena je tudi druga lastnost kopice, da so vsa poddrevesa tudi kopice.

V kopico želimo vstaviti element 5, ki je rdeče obarvan. Ker je 5 manjše od elementa v levem otroku torej 19 in manjše od elementa v desnem otroku torej 12, pravilo kopice ni izpolnjeno.

Po postopku spajanja kopice je potrebno število 5 premakniti v smeri večjega otroka. Na podlagi tega zamenjamo števili 5 in 19.

Tabela po prvem koraku

Opazujemo drevo, ki ima v korenu element 5 (rumeno drevo).

Ker je element v korenu 5 manjši od elementa v desnem otroku (13), zamenjamo elementa 5 in 13.

Tabela po drugem koraku

Drevo s korenom 5 nima otrok, zato zadošča vsem lastnostnim kopice in postopek zaključimo.

Imamo tabelo števil, katera ni nujno da zadošča lastnostim kopice.
Števila bi radi uredili tako, da prvo mesto v tabeli predstavlja koren kopice.

• Postopek:
  

  • Začnemo pri vseh poddrevesih in jih uredimo v kopico, vse dokler tega ne storimo tudi za korenski element --> začnemo pri najnižjih nivojih in spajamo kopice.
    

• PRIMER:
  Imamo naslednjo tabelo:
  
  

  Začetna tabela

  
  Prvo poddrevo, ki ga moramo pregledati, je označeno z zeleno. Vidimo, da je vrednost korena 20 in ima samo enega otroka z vrednostjo 3. Ker je 20 večje od 3, drevo zadošča lastnostim kopice.
  
  

  Tabela po prvem koraku

  
  Naslednje drevo, ki ga pregledamo je označeno z oranžno. To drevo ima v korenu vrednost 10 ter dva otroka z vrednostma 25 in 13. Ker vidimo, da je vrednost korena manjša od vrednosti otrok, premaknemo vrednost korena v smeri večjega otroka (zamenjamo 25 in 10).
  

Tabela po drugem koraku

Postopek ponovimo za drevo s korenom 15. Ker je drevo že kopica (je koren večji od svojih sinov), ni premikanja.

Naslednje poddrevo je poddrevo s korenom 8. Njegova sinova sta 25 in 20. Ker vidimo, da je vrednost korena manjša od vrednosti otrok, premaknemo vrednost korena v smeri večjega otroka (zamenjamo 25 in 8).

Tabela po tretjem koraku

S tem se spremeni še oranžno poddrevo, ki ima sedaj v korenu vrednost 8. Vidimo, da je vrednost korena manjša od vrednosti otrok, premaknemo vrednost korena v smeri večjega otroka (zamenjamo 13 in 8).

Končna tabela

Na koncu ostane drevo s korenom 30, ki ima za otroka 25 in 15 (na sliki označeno z rumeno). To drevo že ustreza lastnostim kopice, zato ni premikanja.

Če je v tabeli shranjena kopica, to pomeni, da je največji element polja na prvem mestu v tabeli. To dejstvo lahko s pridom izkoristimo za urejanje števil v tabeli.

• Postopek:
  

  • Če tabela ne predstavlja kopice, nad poljem izvedemo postopek Zgradi kopico.
    

  • Za vse elemente polja, ki ne predstavljajo listov, ponavljaj:
    

    • Zamenjaj prvi (največji) element polja z zadnjim elementom.
      
    • "Zmanjšaj" velikost kopice za en element.
      
    • Ker smo prvi element premaknili z zadnjega mesta, iz "zmanjšane" tabele zgradimo kopico. To najhitreje storimo, da spojimo prvi element s kopicama s korenom v drugem in tretjem elementu.
      

Uporabili bomo končno tabelo, katero smo s postopkom Zgradi kopico dobili v prejšnjem poglavju. Velikost kopice bomo označevali z zeleno barvo. Ostale elemente, ki ne spadajo več v kopico, bomo označevali z rdečo barvo.

Začetna tabela

V prvem koraku zamenjamo prvi element z zadnjim elementom in spojimo element 3 s kopicama s koreni 25 in 15. Preostale elemente (brez elementa 30) ponovno uredimo po lastnostih kopice.

Tabela po prvem koraku

V vseh naslednjih korakih prvi element zamenjamo z zadnjim elementov. Tabele, ki jih dobimo po vsakem koraku, še uredimo po lastnostih kopice.

Deveti in deseti korak ter končna tabela

• Postopek:
  
  

  • Element dodamo na prvo prosto mesto.
    
  • Nato ga premikamo navzgor po kopici, če je vrednost v staršu elementa manjša.
    
    
• Postopek ponavljamo, dokler ne pridemo do korena ali pa je vrednost v staršu elementa večja od gledane vrednosti. Premikanje navzgor pomeni zamenjavo vrednosti, ki ju gledamo, torej zamenjavo otroka s staršem.
  

• Primer: V spodnjo kopico želimo vstaviti element 17.
  
  

  Vstavljanje elementa v kopico

  
  

• Primer: Vstavljanje elementa 17 v kopico s pomočjo tabele.
  
  

  Vstavljanje elementa v kopico s pomočjo tabele

  
  Novo nastala kopica je povečana za en element glede na začetno kopico. Za vsak element, ki ga želimo vstaviti v kopico, postopek ponovimo.
  

Da iz kopice odstranimo največji element ( koren) si pomagamo s postopkom pod naslovom: Postopek uredi s kopico.

Začetna kopica

1. KORAK

2. KORAK

Ta postopek nadaljujemo, dokler nam ne ostanle le en element, ki predstavlja koren drevesa. Zadnji korak postopka v trenutnem primeru je element 3.

• Omogoča hiter dostop do največjega oziroma najmanjšega elementa.
  
  
• Zagotavlja ugodne logaritemske časovne zahtevnosti za večino ostalih operacij.
  
  
• Pri implementaciji podatkovne strukture prednostna vrsta in pri algoritmu za urejanje z izboljšanim izbiranjem (angleško HeapSort).
  
  
• Na področju ekonomičnega vzdrževanja podatkov, urejenih po velikosti, na primer v operacijskih sistemih in prevajalnikih.