Komplementarni koti
Zveze med kotnimi funkcijami komplementarnih kotov za ostre kote že poznamo:
Želeli bi preveriti, ali ti obrazci veljajo za poljuben kot v enotski krožnici.
Za tope kote je možen geometrijski premislek.
Omenjene zveze pa splošno veljajo, kar bomo zlahka preverili z adicijskimi izreki.
Geometrijski premislek
Naj bo topi kot. V enotski krožnici imamo podana dva kota; in , pri čemer naj bo kot topi kot. Na zgornji sliki si poglejmo trikotnika in . Kot označimo s .
Notranji koti trikotnika so , in . Torej velja:
Geometrijski premislek
Trikotnika in se torej ujemata v vseh treh kotih in najdaljši stranici, ki je polmer enotske krožnice, torej sta skladna trikotnika. Na sliki z miško premikaj točko po enotski krožnici in opazuj skladna trikotnika. Ker sta skladna, se ujemata v vseh treh stranicah.
Torej je in .
Po definiciji kotnih funkcij v enotski krožnici je , , , .
Od tod pa sledi, da je
in
Komplementarni koti
Izpeljimo še obrazce za kosinus, tanges in kotanges komplementarnega kota.
Zapomnimo si, da za poljuben kot veljajo obrazci
Suplementarni koti
Poznamo tudi že zveze med kotnimi funkcijami suplementarnih kotov za ostre kote. Pri osvežitvi spomina si pomagaj s spodnjo sliko.
|
|
Suplementarni koti
Na spodnji sliki vidimo, da kot leži v tretjem kvadrantu. Označen je tudi kot . Z miško klikni na premični krak kota in ga prestavljaj po in kvadrantu. Pri tem opazuj vrednosti sinusa in kosinusa teh dveh kotov.
Suplementarni koti
Opazimo, da veljajo zveze med kotnimi funkcijami suplementarnih kotov za poljuben kot . Naše domneve preverimo še računsko.
Za dokaz zvez med sinusom in kosinusom suplementarnih kotov uporabimo adicijske izreke.
Zapomnimo si, da za poljuben kot veljata obrazca:
S kvocientom teh dveh izrazov pa bi dobili zvezi za tangens in kotangens suplementarnih kotov.
Koti, ki se razlikujejo za
Zanima nas tudi, kako se spreminjajo vrednosti kotnih funkcij, če kotu prištejemo ali odštejemo . Vemo že, da sta tangens in kotangens periodični kotni funkciji z osnovno periodo , kar pomeni, da se vrednosti tangensa in kotangensa ohranita, če kotu prištejemo ali odštejemo osnovno periodo. Torej je: in .
Kaj pa se dogaja z vrednostmi sinusa in kosinusa? Opazuj na slikah.
Koti, ki se razlikujejo za
S slik ugotovimo, da se vrednosti sinusov in kosinusov kotov in razlikujejo samo po predznaku. Enako velja tudi, če primerjamo sinusa in kosinusa kotov in .
Koti, ki se razlikujejo za
Kratek dokaz za naše ugotovitve:
Zapomnimo si, da za poljuben kot veljajo tudi obrazci
Prehod na ostri kot
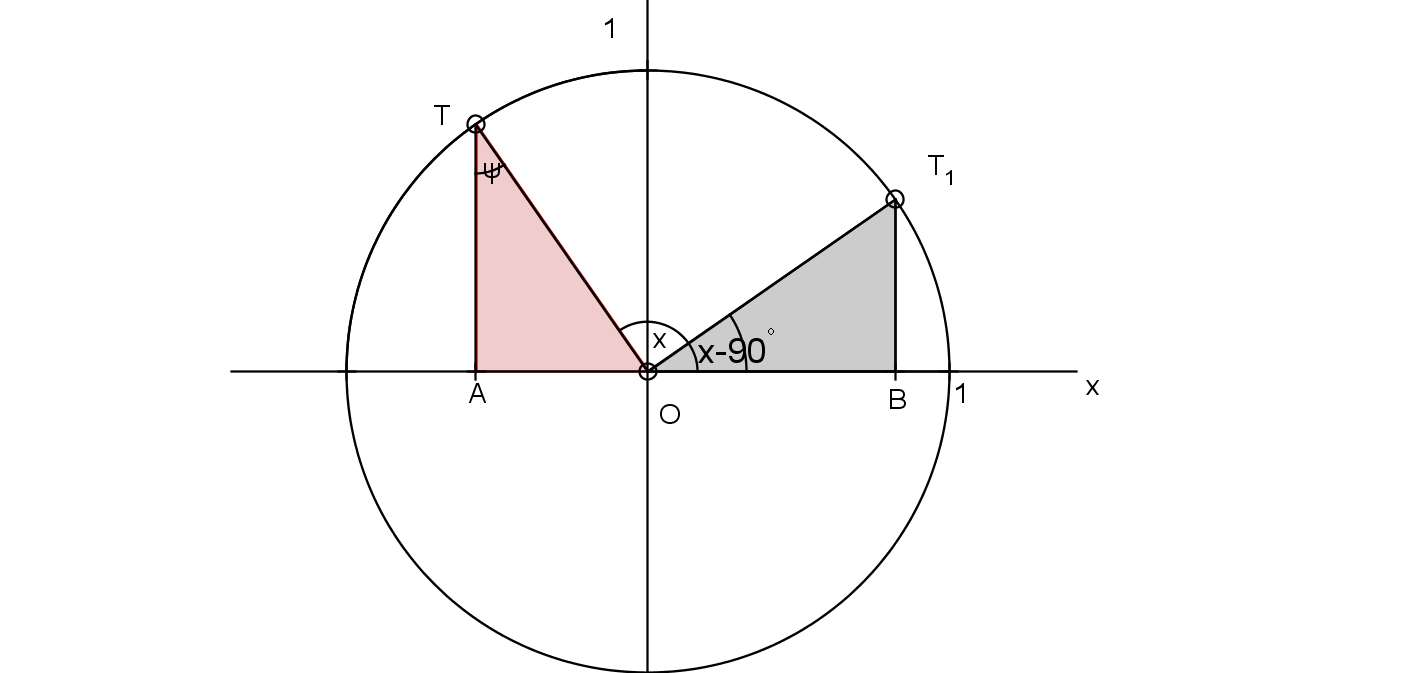
Zgornja slika nam prikazuje, kako bi izračunali vrednost trigonometrične funkcije pri poljubno velikem kotu. Najprej bi uporabili periodičnost, s tem prevedemo izraz na trigonometrično funkcijo kota med in . Pri kotih med in uporabimo zveze med kotnimi funkcijami kotov, ki se razlikujejo za . S tem dobimo kotno funkcijo, izraženo s kotom med in . Upoštevamo zveze med kotnimi funkcijami suplementarnih kotov in dobimo kotno funkcijo, izraženo z ostrim kotom. Če uporabimo še komplementarnost, dobimo izraz s kotno funkcijo, izraženo s kotom med in .
Oglejmo si primer, kako bi natančno izračunali vrednost .
Najprej uporabimo lastnost, da je sinus periodična kotna funkcija z osnovno periodo . Torej je
.
Nato uporabimo zveze med kotnimi funkcijami suplementarnih kotov in dobimo:
.
Tangens je liha in periodična kotna funkcija z osnovno periodo .
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Super, rešitev je pravilna.
Rešimo nekaj primerov
Najprej izračunaj posamezne vrednosti kotnih funkcij z upoštevanjem lastnosti posameznih kotnih funkcij in uporabo zvez med kotnimi funkcijami.
Ko si izračunal vrednosti vseh kotnih funkcij, vstavi dobljene vrednosti v ulomek in zapiši rezultat.
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
a) Sinus je liha kotna funkcija z osnovno periodo .
b) Tangens je periodična kotna funkcija z osnovno periodo .
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Rešimo nekaj primerov
Najprej izraz poenostavi in ga zapiši kot enočlenik.
Nato uporabi adicijski izrek za sinus razlike.
Potrebuješ še vrednost sinusa in kosinusa kota , ki ga izračunaš s pomočjo tangensa. Nato vstaviš izračunane vrednosti v izraz in dobiš rezultat.
Super, rešitev je pravilna.
1. naloga
Natančno izračunaj vrednost izraza.
Super, rešitev je pravilna.
2. naloga
Izrazi s kotno funkcijo kota, manjšega od oziroma .
Super, rešitev je pravilna.
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
Super, rešitev je pravilna.
To pa ne bo držalo. Rešitev je:
4. naloga
Super, rešitev je pravilna.
To pa ne bo držalo.
Poenostavljen izraz je:
Super, rešitev je pravilna.
Rezultati
