Edsger Wybe Dijkstra (1930-2002)
|
|
Najkrajše poti v uteženem grafu (Dijkstra)
ZGODOVINA
OBRAZLOŽITEV GLAVNIH POJMOV
Graf () je množica vozlišč (), ki so med seboj povezana s povezavami (). Matematični zapis za graf je . Povezave so lahko usmerjene ali neusmerjene.
|
|
Usmerjen graf je tisti graf, ki ima vse povezave usmerjene. In posledica je, da se lahko iz ene točke premaknemo v drugo le v smeri povezave, nazaj pa po isti poti ne gre, razen če je le ta dvosmerna.
|
|
Utežen graf je tisti graf, ki ima na vseh povezavah neko težo (npr. ceno, razdaljo). Ta nam pove koliko enot porabimo, da pridemo iz ene točke v drugo.
|
|
NAJKRAJŠA POT (ang. Shortest path)
Najkrajša pot na grafu je tista, ki iz ene točke pride v drugo tako, da je vsota vseh uteži na izbranih povezavah najmanjša.
| Primer: Zanima nas katera pot je od A do C najkrajša. Najprej pogledamo vse možnosti. Možne izbire so ABC, AC, ADC in AEDC. Sedaj pogledamo vrednosti uteži.
Med vsemi možnostmi izberemo ABC, saj ima ta najmanjši seštevek uteži (4). |
Iskanju najkrajših poti rečemo kar problem najkrajših poti. Tu iščemo najbolj optimalno vrednost.
Poznamo pa seveda več različic tega problema:
- Najkrajše poti iz enega vozlišča
- Najkrajše poti do danega vozlišča
- Najkrajša pot med parom vozlišč
- Najkrajša pot med vsemi možnimi pari vozlišč
OPOMBA: Da je pot najkrajša, ne pomeni, da vsebuje najmanj povezav, ampak da je vsota uteži na povezavah najmanjša.
Za reševanje najkrajših poti poznamo tri algoritme:
- Dijkstrov algoritem (Iskanje najkrajše poti od nekega vozlišča le za nenegativne uteži.)
- Bellman-Fordov algoritem (Iskanje najkrajše poti od nekega vozlišča tudi za negativne uteži.)
- Floyd-Warshallov algoritem (Iskanje najkrajših poti med vsemi pari vozlišč s poljubnimi utežmi.)
DIJKSTROV ALGORITEM
Dijkstrov algoritem najde najkrajše poti iz izbrane točke do vseh ostalih točk. Med izvajanjem postopka gradimo drevo najkrajših poti.
Drevo najkrajših poti je vpeto drevo, ki vsebuje vse najkrajše poti iz izbranega vozlišča do vseh ostalih.
|
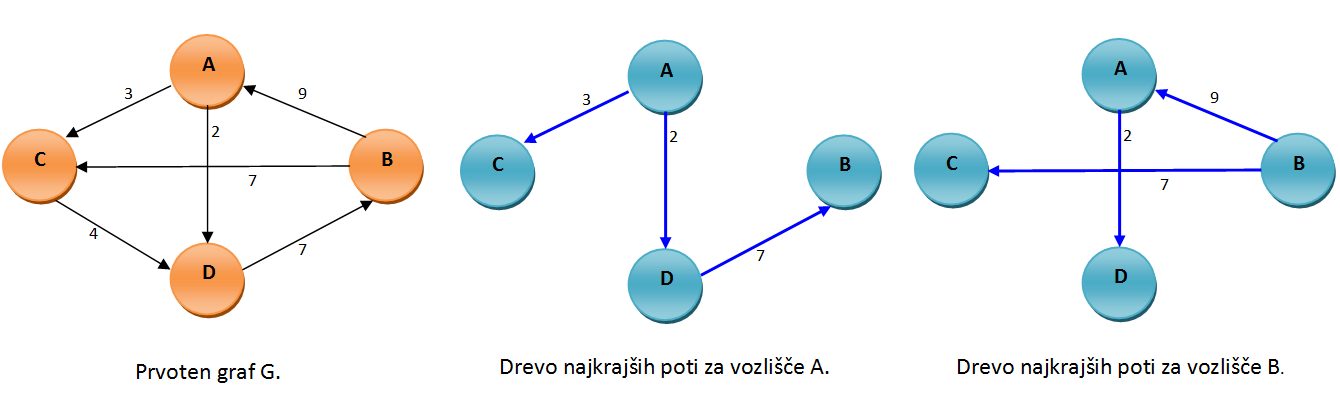
Primer: Zgornja slika nam prikazuje graf G ter dve drevesi najkrajših poti. Pri drugi sliki vidimo drevo najkrajših poti za vozlišče A. Ta nam pove vse najkrajše povezave do preostalih točk. Če nas zanima za koliko je oddaljen C od A vidimo da za 3. Če nas zanima razdalja do B opazimo, da moramo najprej v točko D nato šele v B. In razdalja je 9. Tretji graf pa nam prikazuje drevo najkrajših poti za vozlišče B. Da je tudi tu razdalja od B do A devet, je zgolj naključje. To načeloma ne drži. Opazimo, pa da je tu povezava od B do C, ki je v prejšnjem drevesu ni.
Ugotovitev: Če gledamo drevo najkrajših poti za vozlišče α ne bomo dobili prave najkrajše poti od vozlišča β do γ. V primeru, da bo rešitev prava pa bo to zgolj naključje oz. vsako vozlišče ima svoje drevo najkrajših poti.
Uporaba:
- Iskanje najkrajše poti iz enega kraja v drugega (utež: število kilometrov)
- Iskanje najhitrejše poti iz enega kraja v drugega (utež: čas)
- Iskanje najkrajše poti v omrežjih (začetno in končno vozlišče sta enaka, želimo pa da najhitreje pridemo čez vsa vozlišča).
DIJKSTROV ALGORITEM
Legenda oznak na grafih
ALGORITEM
Algoritem zgradi drevo tako, da vsakič doda iz množice vozlišč, ki še niso v drevesu vozlišče, ki ima najkrajšo pot od začetnega vozlišča.
Dogovor: Zmenimo se, da bodo vozlišča in povezave obarvane glede na legendo iz prejšnje prosojnice. Ob vsakem koraku pa bomo tudi zapisali vrednost najkrajših povezav do posameznih vozlišč.
DELOVANJE ALGORITMA:
Podano imamo:
- množico izbranih vozlišč (modra vozlišča)
- množico kandidatk za izbrano vozlišče (rdeča vozlišča)
- množico prostih vozlišč (oranžna vozlišča)
- začetno vozlišče
Postopek:
- začetno vozlišče damo v množico
- začetnemu vozlišču poiščemo kandidate za povezave in vozlišča do katerih vodijo, ter jih dodamo v množico in izbrišemo iz množice
- vsem vozliščem iz množice izračunamo najkrajšo pot od začetnega vozlišča
- med vsemi vozlišči iz izberemo tistega, ki ima najkrajšo pot (najmanjšo vrednost)
dokler nista množici in prazni izvajaj:
poiščemo nove kandidate za povezave in vozlišča in jih dodamo v množico in izbrišemo iz množice
če najdemo neko kandidatko za izbrano povezavo, ki vodi do vozlišča,ki je že v potem:
če je vrednost najkrajše poti večja kot prejšnja potem
- pustimo prejšnjo vrednost
če pa je vrednost najkrajše poti manjša kot prejšnja potem
- spremenimo na novo vrednost
- izberemo iz množice vozlišče z najmanjšo vrednostjo najkrajše povezave od začetnega vozlišča in ga damo v množico in izbrišemo iz množice .
- algoritem nam vrne drevo najkrajših poti
Bolj podrobno o delovanju algoritma - predstavitev s pomočjo zgleda
Bolj podrobno o delovanju algoritma - predstavitev s pomočjo zgleda
Najprej si izberemo začetno vozlišče (). Nato poiščemo vse povezave, ki vodijo iz njega. Vozlišča, do katerih vodijo te povezave obarvamo rdeče in izračunamo vrednost najkrajše poti od A do njih.
|
|
Od možnih kandidatov izberemo vozlišče, ki ima najmanjšo vsoto uteži povezav od začetne točke. V našem primeru je to vozlišče , saj je vrednost povezave enaka dve. Torej povezava ne ustreza, saj je krajša (). Sedaj poiščemo iz nove izbrane točke () nove možne povezave. In preverimo vrednost najkrajše povezave. V primeru, da je pot iz začetne točke preko nove daljša kot prva, potem vrednosti ne spreminjamo, sicer pa jo.
|
|
V našem primeru se pojavita dve novi možni kandidatki za povezavo ( in ) in eno dodatno vozlišče ().Vrednost povezave do točke B se spremeni iz na , saj ugotovimo, da je krajše, če gremo iz v in nato v . Sedaj med vsemi možnimi kandidatkami (, in ) izberemo tisto vozlišče, ki ima najmanjšo vsoto uteži povezav od do njega. Torej v našem primeru je to vozlišče , ki ima vrednost ne pa , ki ima . Sedaj ponovno poiščemo možne kandidatke za najkrajšo povezavo. To so in .
|
|
Ugotovimo po kateri poti je najkrajše priti do tega vozlišča. Za ta primer je najkrajša pot od do kar preko točke , zato izberemo za naslednjo povezavo.
|
|
Postopek ponavljamo dokler niso povezana vsa vozlišča. S tem se algoritem KONČA.

1. PRIMER
Rešili bomo preprost primer s petimi vozlišči. Iskali bomo najkrajše poti iz točke A do preostalih.
Prikaz rešitve:
|
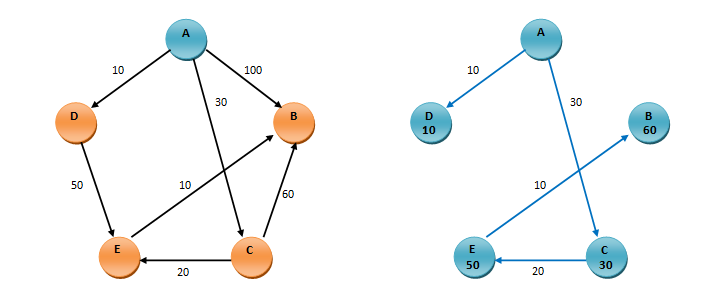
Obrazložitev:Dobljena rešitev je drevo najkrajših poti. Iz grafa razberemo, da so razdalje med točkami sledeče: AB = 60 (A-C-E-B), AC = 30 (direktno), AE = 50 (A-C-E) in AD = 10 (direktno).
OPOMBA: (A-C-E-B) pomeni, da iz točke A pridemo v B tako, da gremo najprej v C, nato v E in iz E v B.
Spodaj si lahko v filmčku ogledate potek reševanja po korakih.
2. PRIMER
Rešili bomo primer s šestimi vozlišči. Iskali bomo najkrajše poti iz točke A do preostalih.
Prikaz rešitve:
|
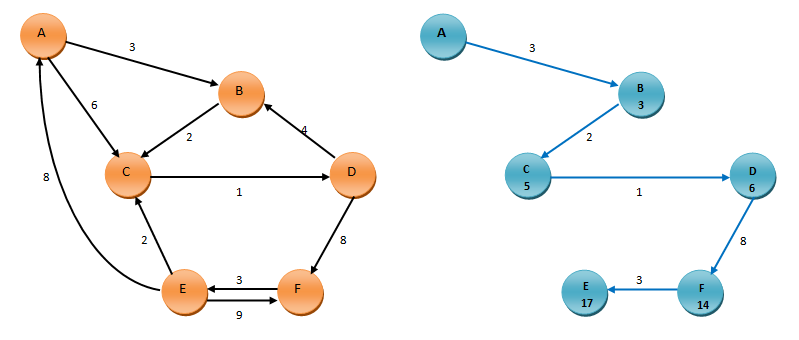
Obrazložitev:Iz drevesa najkrajših poti razberemo, da so razdalje med točkami sledeče: AB = 3 (direktno), AC = 5 (A-B-C), AD = 6 (A-B-C-D), AE = 17 (A-B-C-D-F-E) in AF = 14 (A-B-C-D-F).
Spodaj si lahko v filmčku ogledate potek reševanja po korakih.
3. PRIMER
Rešili bomo nekoliko težji primer z devetimi vozlišči. Iskali bomo najkrajše poti iz točke A do preostalih.
Prikaz rešitve:
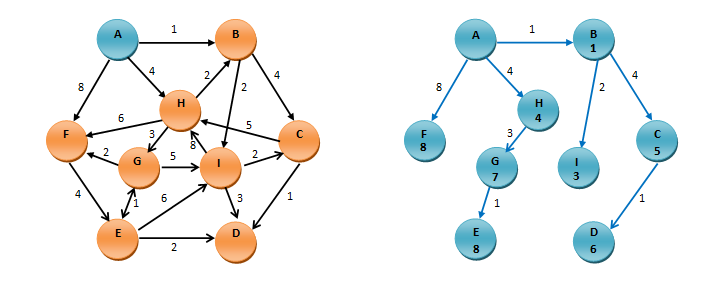
|
Obrazložitev:Iz drevesa najkrajših poti razberemo, da so razdalje med točkami sledeče: AB = 1 (direktno), AC = 5 (A-B-C), AD = 6 (A-B-C-D), AE = 8 (A-H-G-E), AF = 8 (direktno), AG = 7 (A-H-G), AH = 4 (direktno) in AI = 3 (A-B-I).
Spodaj si lahko v filmčku ogledate potek reševanja po korakih.

KVIZ
Pravilno
Vaša rešitev je pravilna. NaprejNapačno
Izbira ni pravilna. Ponovno Namig: Odgovor najdeš na naslednji prosojnici.
Pravilno
Vaša rešitev je pravilna. NaprejNapačno
Izbira ni pravilna. Ponovno Namig: Odgovor najdeš na naslednji prosojnici.
Pravilno
Vaša rešitev je pravilna. NaprejNapačno
Izbira ni pravilna. Ponovno Namig: Odgovor najdeš na naslednji prosojnici.
4. Katera od spodnjih slik predstavlja drevo najkrajših poti vozlišča za graf ?
|
|
Pravilno
Vaša rešitev je pravilna. Zaključi kvizNapačno
Izbira ni pravilna. Ponovno Namig: Pozoren/na bodi na vrednost povezave od izbrane točke do opazovane. Odgovor najdeš na naslednji prosojnici.
VIRI
- Zapiski iz predavanj iz predmeta Optimizacija, študijsko leto 2010/2011
- Jernej Kozak, Podatkovne strukture in algoritmi, DMFA, ljubljana 1986
- Dijkstra's Shortest Path Algorithm
- Primoz Umek, PSIA-seminarska naloga, Dijkstrov algoritem.pdf
- Bojan Možina, Najkrajše poti in algoritem Bellman-Ford
- DIJKSTRA ALGORITHM
- Wikipedija - Dijkstrov algoritem
- Dijkstra R2Wiki
- MY liTTleBloG