Zapišite vse ničle polinoma p(x)=x(x-2)(x-3),xϵR. V katerih točkah seka premica y=3-x graf polinoma p(x)?
Matematična naloga
Besedilo naloge
Reševanje brez programa: Ničle polinoma
Ker je polinom p(x)=x(x-2)(x-3), ze razstavljen, ničle samo preberemo:
- x1=0
- x2=2
- x3=3
Rešitev Ničle polinoma so: 0,2 in 3.
Reševanje brez programa: Presečišče polinoma in premice
Presečišče polinoma in premice izračunamo tako, da enačbi med seboj izenačimo, na ta način dobimo točke abscisne osi:
- p(x)=y
- x(x-2)(x-3)=3-x
- (x2-2x)(x-3)=3-x
- x3-3x2-2x2+6x=3-x
- x3-5x2+7x-3=0
Razstavimo s pomočjo Hornerjevega algoritma:

- (x-1)(x2-4x+3)=0
- (x-1)(x-1)(x-3)=0
- x1=x2=1 in x3=3 Za x1 in za x2 dobimo 1, kar pomeni, da se v tej točki polinom in premica dotikata.
Nato x1 in x3 vstavimo v eno izmed začenih enačb (y=3-x):
x1=x2=1: y=3-1=2
- Dobimo prvo presečišče P1(1,2)-dotikališče.
x3=3: y=3-3=0
- S tem dobimo drugo presečišče P2(3,0).
Rešitev Presečišči polinoma in premice sta P1(1,2) in P2(3,0).
Reševanje s programom GeoGebra: Ničle polinoma
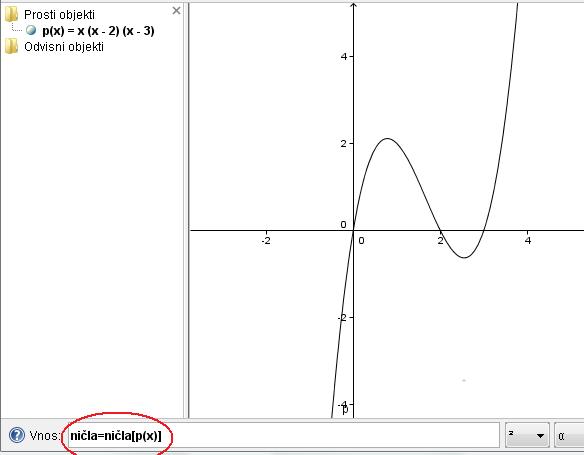
V program vpišemo enačbo p(x)=x(x-2)(x-3). S tem nam program nariše polinom. Že iz slike je razvidno, kje so ničle polinoma. Z ukazom Ničla[], pa ničle še označimo in s tem dobimo rešitev prvega dela naloge.
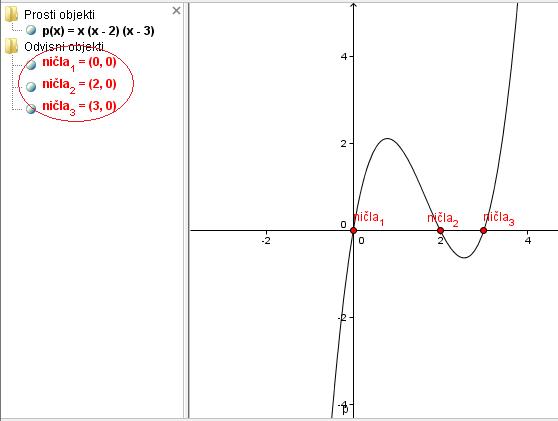
Rešitev Ničle polinoma so: 0, 2, 3.
Reševanje s programom GeoGebra: Presečišče polinoma in premice
Nato v program vpišemo še premico y=3-x. S tem nam program nariše premico. Že iz slike je razvidno, kje sta presečišči obeh enačb. Z ukazom Presečišče[], pa presečišči še označimo in s tem dobimo rešitev naloge.
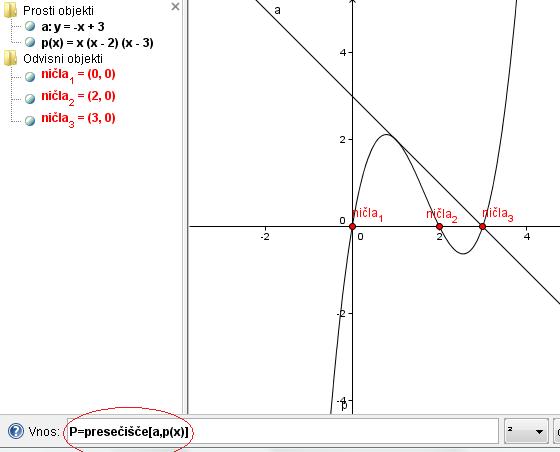
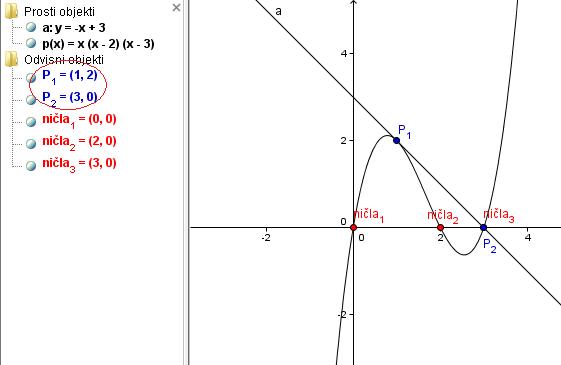
Rešitev Presečišči polinoma in premice sta P1(1,2) in P2(3,0).