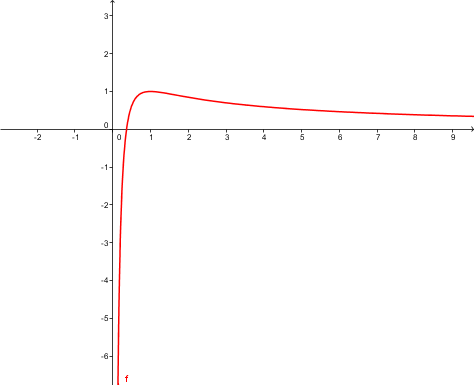
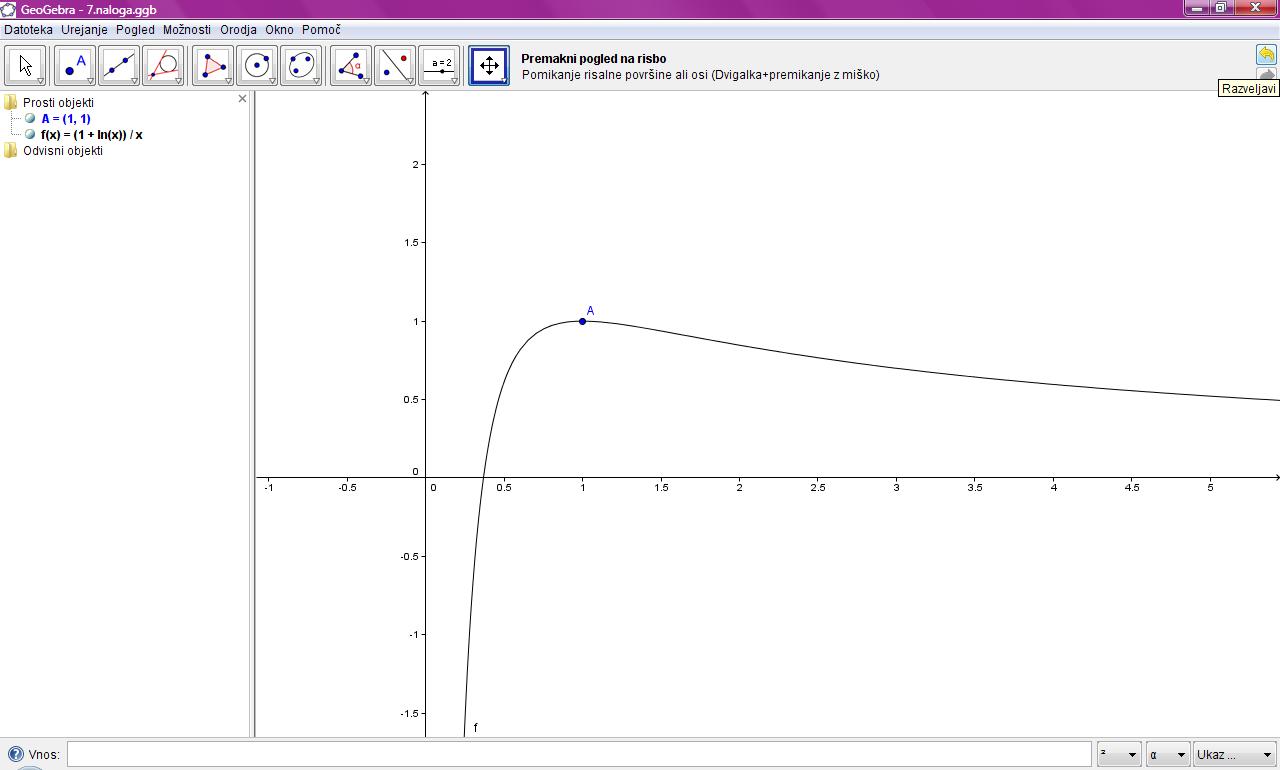
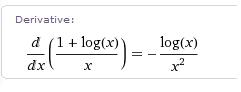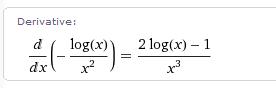Dana je funkcija
- Poiščite definicijsko območje funkcije in izračunajte njen prvi in drugi odvod.
- Izračunajte, pod kolikšnim kotom seka krivulja os . Rezultat zapišite na minuto natančno.
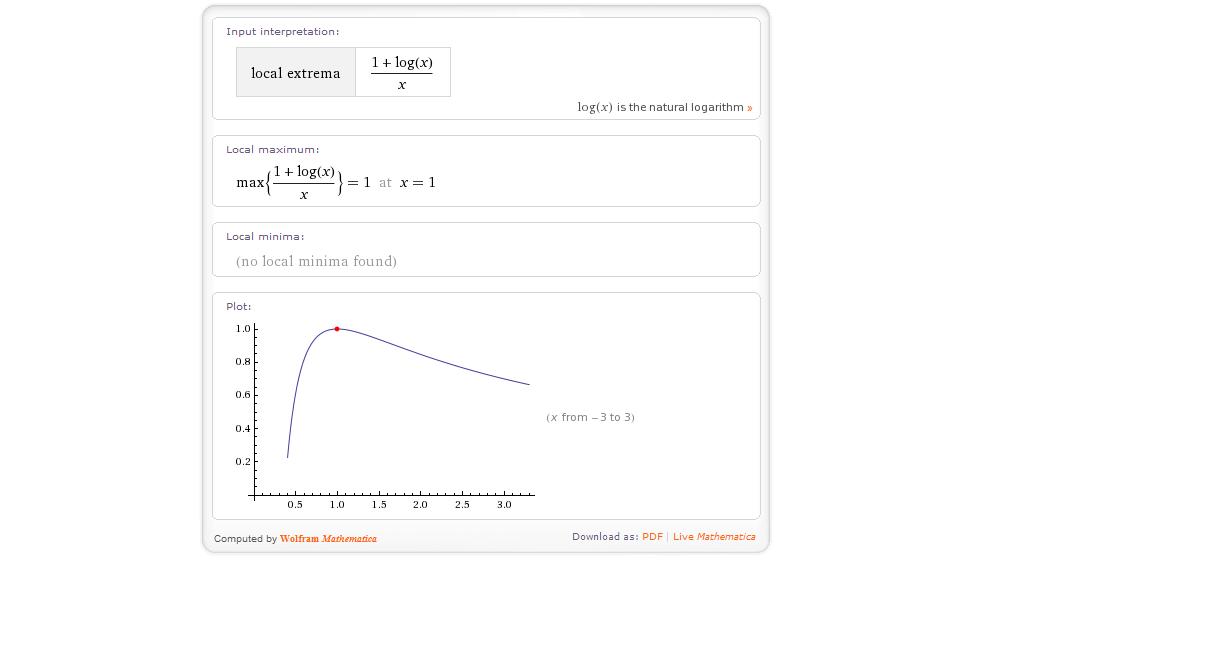
- Poiščite lokalne ekstreme funkcije .
- Poiščite intervale naraščanja funkcije .
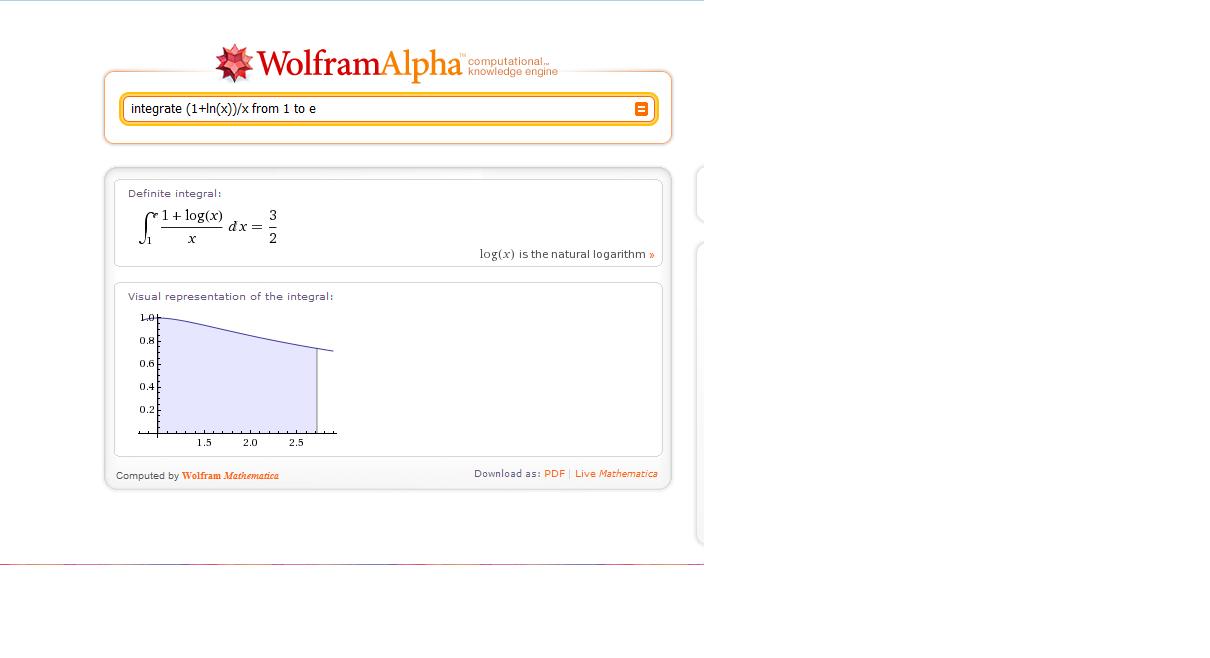
- Izračunajte ploščino lika, ki ga omejujejo krivulja , os x ter premici in .