Dani sta funkciji f(x)=x^2-4x+3 in g(x)=-3x+5.
- a) Nariši njuna grafa v isti koordinatni sistem.
- b) Izračunaj in zapiši presečišči.
- c) Reši neenačbo: f(x)>g(x).
Besedilo naloge
Dani sta funkciji f(x)=x^2-4x+3 in g(x)=-3x+5.
Reševanje brez programa: graf
Ničle:
Začetna vrednost:
Teme:
q= -D/4a=-4/4= -1
Če želimo narisati graf funkcije g(x) moramo izračunati najmanj dve točki, skozi kateri gre premica:
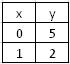
Graf:
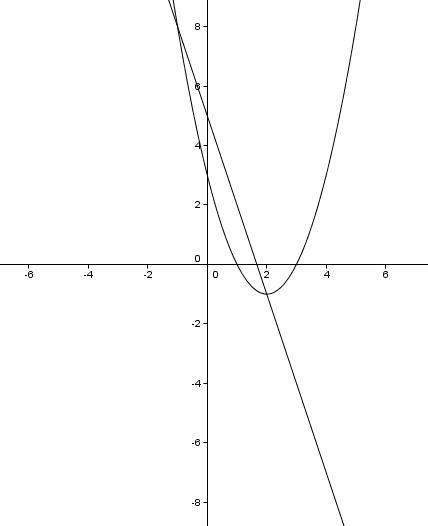
Reševanje brez programa: presečišči
Presečišče grafa f(x) in g(x)izračuanmo tako, da enačbi izenačimo. Na ta način dobimo točke na abscisni osi:
Nato x vstavimo v eno izmed enačb:
Dobimo presečišči funkcija g(x) in f(x):
Reševanje brez programa: neenačba: f(x)>g(x)
Neenačba: f(x)>g(x)
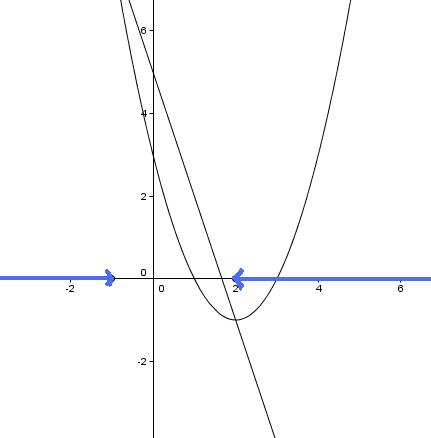
Iz slike preberemo rešitev: x∈(-∞,-1)∪(2,∞)
Reševanje s programom GeoGebra: graf
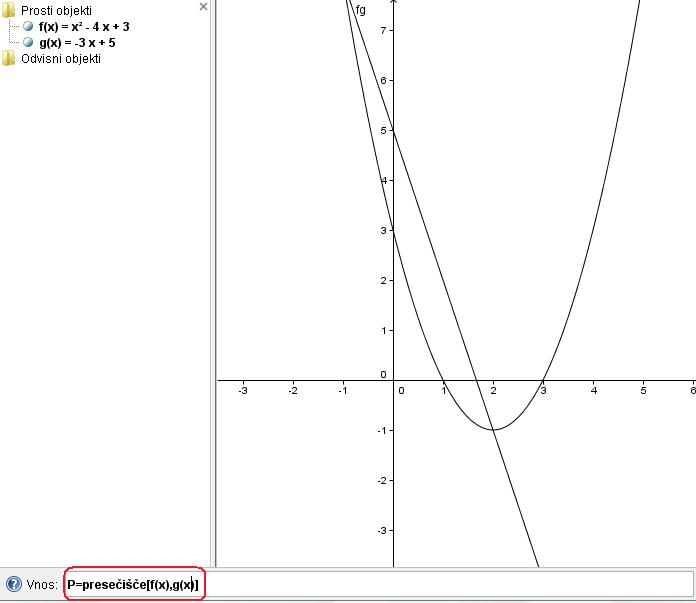
V program vpišemo podani funkciji f(x)=x^2-4x+3 in g(x)=-3x+5. S tem nam program nariše funkciji f(x) in g(x).
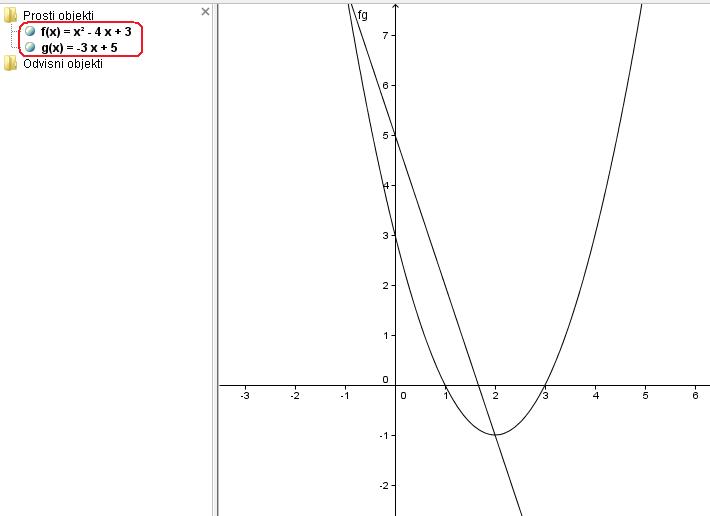
Reševanje s programom GeoGebra: presečišči
Presečišči funkcije f(x) in g(x) izračunamo z ukazom Presečišče[].
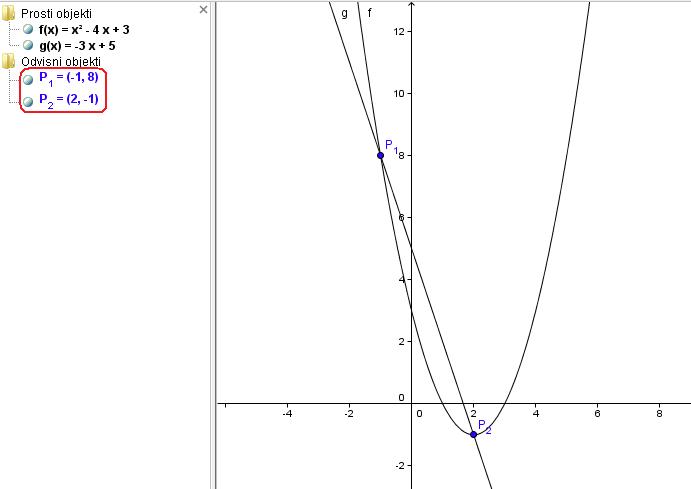
Reševanje s programom GeoGebra: neenačba: f(x)>g(x)
V programu GeoGebra ne moremo izračunati neenačbo f(x)>g(x),
lahko pa iz slike preberemo, kje je graf funkcije f(x)>g(x).
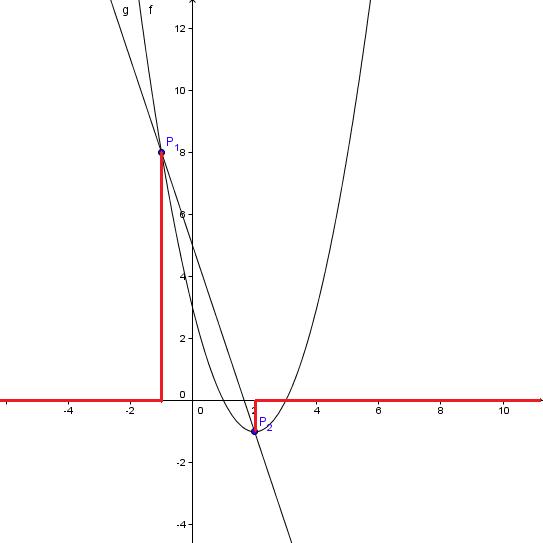
Iz slike preberemo rešitev: x∈(-∞,-1)∪(2,∞)