• Rdeče-črno drevo (v nadaljevanju RČD) je delno poravnano dvojiško iskalno drevo.

• Barva ni dovolj, da govorimo o RČD, potrebnih je še nekaj lastnosti. In to so:

  • koren drevesa je črne barve,
  • rdeče vozlišče sme imeti samo črne sinove,
  • vsi listi drevesa so črne barve,
  • za vsako vozlišče mora veljati, da vsaka pot od vozlišča do praznega poddrevesa vsebuje enako število črnih vozlišč.

• Primer RČD:

• Operacije, ki se izvajajo na RČD so iskanje, vstavljanje in brisanje.

• V RČD se rotacije pogosto uporabljajo. Rotacija zamenja vlogo očeta in sina. V splošnem poznamo levo in desno rotacijo, ki sta si nasprotni.

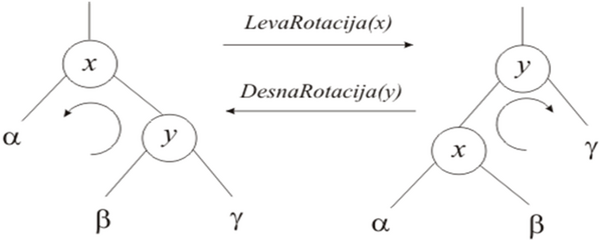
• Ko v RČD vstavimo vozlišče (to je trenutno vozlišče), ga vedno obarvamo rdeče. Pri tem pa pogosto pridemo do primera, ko ima rdeče vozlišče rdečega sina (kar pa pri RČD ne sme biti).
• Kako odpraviti 'napako' in pridti do RČD?
• V primeru, da je oče trenutnega vozlišča črn problema ni.
• Če je oče trenutnega vozlišča rdeče barve in dedek ne obstaja, očeta pobarvamo črno in je problem odpravljen.
• Če sta oče in stric trenutnega vozlišča rdeče barve, dedka obarvamo rdeče, očeta in strica pa črno. Po postopku prebarvanja dedek postane trenutno vozlišče in postopek rekurzivno ponovimo.

• Če je stric črn ali ga ni, ločimo 2 primera:

  • Oče trenutnega vozlišča A je desni sin svojega očeta in ločimo 2 podprimera:

    • Vozlišče A je levi sin, njegov oče postane trenutno vozlišče. Nad njim izvedemo desno rotacijo, nato njegovega očeta obarvamo črno, dedka obarvamo rdeče. Nad dedkom izvedemo še levo rotacijo.
    • Vozlišče A je desni sin. Njegovega očeta obarvamo črno, dedka rdeče. Nad dedkom izvedemo levo rotacijo.

  • Oče trenutnega vozlišča A je levi sin svojega očeta:

    • Vozlišče A je levi sin. Očeta od vozlišča A obarvamo črno ter dedka rdeče. Nad dedkom izvedemo še desno rotacijo.
    • Vozlišče A je desni sin in njegov oče postane trenutno vozlišče ter nad njim izvedemo levo rotacijo. Očeta obarvamo črno, dedka rdeče ter nad dedkom izvedemo desno rotacijo.

• Ker je RČD dvojiško iskalno drevo, vedno velja, da je vrednost v nekem vozlišču vedno večja od vrednosti v levem sinu, ter vedno manjša od vrednosti v desnem sinu.
• Z iskanjem začnemu v korenu. Če je vrednost, ki je iščemo večja od korena, nadaljujemo v desno poddrevo, če pa je vrednost manjša, nadaljujemo v levo poddrevo.

• Primer, kako v spodnjem RČD najdti element 9.

• Ker je 9 več od 8, nadaljujemo v desno podrevo in pridemo do 12. Ker je 9 manj od 12, gremo v levo poddrevo. In tako smo prišli do 9.

• Primer, kako v spodnje RČD vstaviti element 9.

• Postopek poteka na podoben način kot pri iskanju. Če je vrednost, ki je vstavljamo večja od korena (oz. trenutnega vozlišča) gremo v desno poddrevo, sicer gremo v levo poddrevo. Ko pridemo do listov vozlišča obarvamo vozlišče rdeče in dodamo 2 črna sinova brez vrednosti (nil).

• Ker sta oče in stric rdeče barve, ju prebarvamo na črno, ter dedka prebarvamo na rdeče.

Primer, kako zgradimo RČD s podatki: 5, 12, 6, 3, 10 in 11.

Primer, kako zgradimo RČD s podatki: 2, 12, 8, 1, 9, 13, 4, 7, 15, 10, 18, 3, 5, 16, 20, 11, 17, 19, 21, 6 in 14.

• 2 postavimo v koren in ga obarvamo črno. Korenu dodamo 12 in sicer postane to desni sin.

• Dodamo 8. Oče rdeč, strica ni, trenutno vozlišče je levi sin, njegov oče pa je desni sin svojega očeta, zato nad očetom izvedemo desno rotacijo. Po rotaciji očeta od 12 obarvamo črno, dedka rdeče in nad dedkom izvedemo levo rotacijo.

• Vstavimo 1. Oče in stric sta rdeča, zato ju obarvamo črno, dedka rdeče. Ker je dedek koren, ga obarvamo nazaj črno in s tem dobimo pravo RČD.

• Pri vstavljanju 9, 13 in 4 ni posebnosti.

• Vstavimo 15. Oče in stric sta rdeča zato ju obarvamo črno, dedka pa obarvamo rdeče.

• 10 vstavimo brez posebnosti.

• Vstavimo 18. Vstavljeno vozlišče je desni sin, njegov oče je prav tako desni sin njegovega očeta, zato očeta od 18 obarvamo črno, dedka rdeče in nad dedkom izvedemo levo rotacijo.

• Vstavimo 5. Oče in stric sta rdeča, zato ju obarvamo črno, dedka pa rdeče. Po prebarvanju dedek od 5 postane trenutno vozlišče (torej 4). Njegov oče in stric sta rdeča, zato postopek prebarvanja ponovimo.

• Vstavimo 11, očeta obarvamo črno, dedka rdeče in nad dedkom izvedemo levo rotacijo.

• In končno drevo:

  OPOMBA: Po pravilih bi morala na vsakem koraku vsakemu dodanemu vozlišču dodati 2 črna vozlišča brez vrednosti.

Ena od lastnosti RČD je:

Preveri

Ali je na spodnji sliki prikazano pravo RČD?

Preveri

Katere od naslednjih trditev so pravilne:

Preveri

• http://rc.fmf.uni-lj.si/matija/OpravljeneDiplome/Petra_Tome_Diploma.pdf
• Jani Cerar: Rdeče-črna drevesa - diplomsko delo, Maribor 2010
• http://penelope.fmf.uni-lj.si/r2wiki/index.php/Glavna_stran/SeminarskeNaloge/2009_1sem/Rde%C4%8De-%C4%8Drno_drevo/ime2
• Igor Kononenko, Marko Robnik Šikonja: Algoritmi in podatkovne strukture, Ljubljana 2003