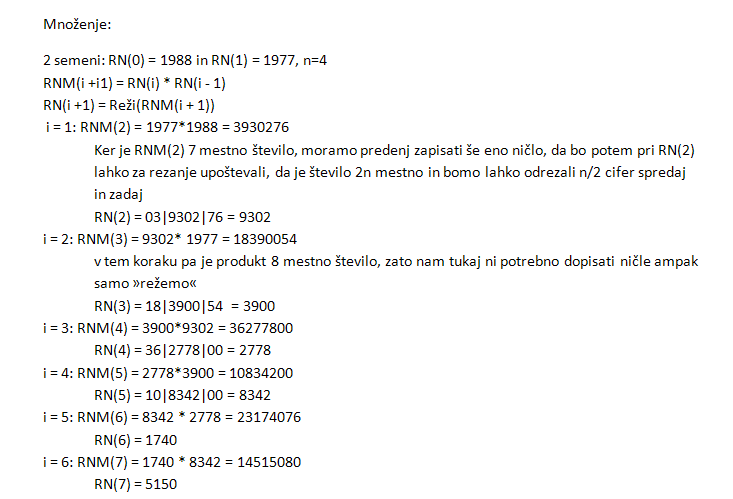
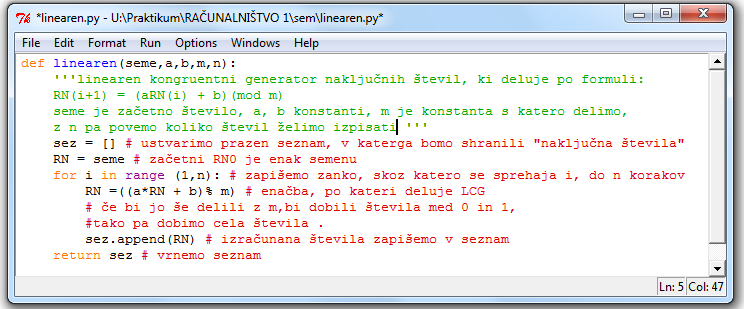
Naključna števila so števila, ki se brez nekega smisla ali pravila podana z nekim zaporedjem. V nobenem primeru ne moremo napovedati naslednjega števila. Taka števila dobimo s pomočjo pojavov v naravi in računalniški tehnologiji. Praviloma so porazdeljena na pol zaprtem intervalu od 0 do 1 – [0,1). Takšna števila pravzaprav niso naključna števila ampak so psevdo-naključna števila. To pomeni, da so napovedljiva na znano pravilo, po katerem so narejena. Psevdo pa iz slovarja slovenskega knjižnega jezika pomeni:
psevdo... predpona v sestavljenkah
(e) nanašajoč se na a) lažen,
navidezen: psevdodemokracija,
psevdoznanstven b) nepravi, nepristen:
psevdogotika, psevdonaroden
Edini način za res naključna števila pa je potrebna uporaba fizikalnega procesa, ki je sam po sebi naključen. Primer takega načina je metanje kovanca ali kocke.

|

|