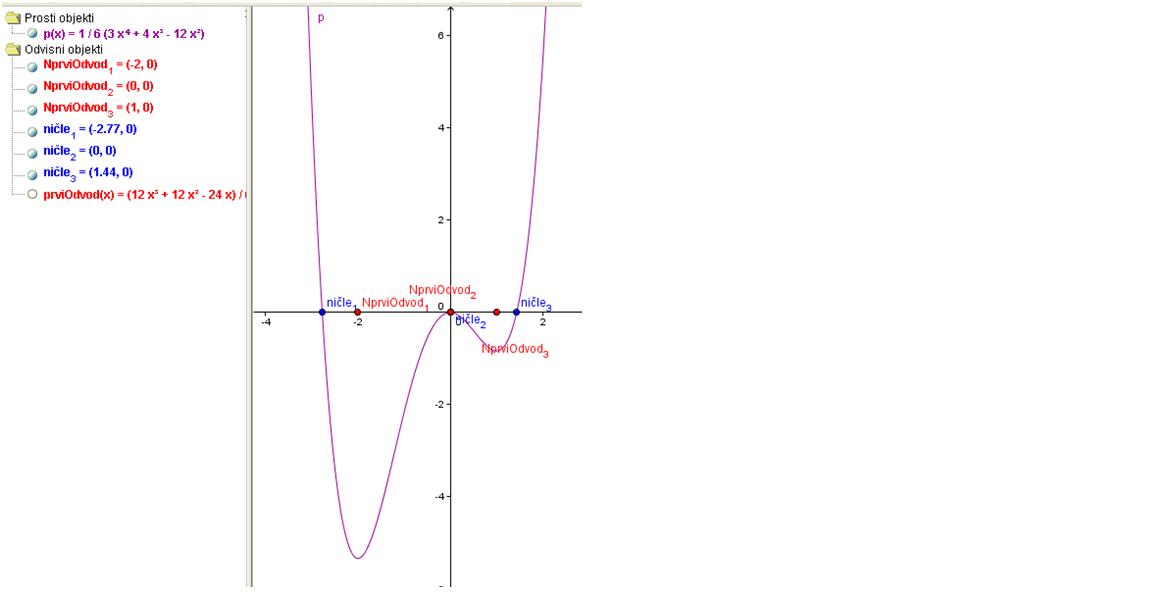
Podan je polinom z enačbo . Nariši njegov graf in poišči naslednje:

• a) ničle polinoma,
• b) stacionarne točke
• c) intervale konveksnosti in konkavnosti.

Postopek reševanje naloge in rešitev:

• Pri reševanju naloge sem si pomagala s programom GeoGebra.

• Najprej sem nalogo rešila po peš poti in porabila kar nekaj časa, da sem prišla do rešitve. Zato je pri iskanju ničel, prevojev in stacionarnih točk polinoma višje stopnje veliko bolj učinkovito reševanje s pomočjo programa npr. Geogebra, ki ti s pomočjo preprostih ukazov poišče vse zahtevane podatke.

• Pri reševanju po peš poti moramo pri večjih stopnjah polinomov paziti,da se ne zmotimo pri računanju. Seveda pa moramo pri računaju po peš poti poznati določena pravila npr. Kot je določanje konveksnosti, konkavnosti, uporabe odvoda pri iskanju prevojev in stacionarnih točk.

• V nadaljevanju bom navedla kako sem iskane podatke dobila po peš poti in kako s pomočjo programa GeoGebra.

Rešitev točke a:

• Najprej sem ničle polinoma poiskala po peš poti in dobila naslednje rešitve: dvojna ničla za f, , , Vrednost tretje in četrte ničle sem zaokrožila na dve decimalni mesti.

• V GeoGebri sem ničle poiskala na naslednji način: Najprej sem narisala graf polinoma( v vnosno vrstico sem vnesla enačbo polinoma Da so se mi izpisale na sliki ničle polinoma sem v vnosno vrstico vnesla ukaz ničle=Ničla[p(x)].

• Pri podanih ničlah in risanju grafa moramo upoštevati, da polinom zamenja predznak v ničlah lihe stopnje.

Rešitev točke b:

• Stacionarne točke polinoma sem po peš poti poiskala s pomočjo definicije o stacionarni točki, ki pravi: Točko, v kateri prvi odvod funkcije zavzame vrednost 0, imenujemo stacionarna točka. Če je stacionarna točka.

Če je je stacionarna točka,potem:

1. Če je levo od odvod f´ pozitiven, desno od pa negativen, ima f v lokalni Maksimum. 2. Če je levo od odvod f´ negativen, desno od pa pozitiven ima f v lokalni Minimum. 3. Če v točki x_0 odvod f´ ne menja predznaka, v x_0 ni ekstrama.

• Po peš poti sem izračunala ničle prvega odvoda in dobila: 2x(x+2)(x-1)=0 Ničle prvega odvoda so stacionarne točke v točkah -2,1,0. Nato sem na intervalih x>1, 0<x<1 in x>1, preverila predznak odvoda in dobila da ima v točki -2 minimum, v točki 0 maksimum in, da je v točki 1 minimum funkcije.

• Ničle prvega odvoda so na spodnji sliki prikazane z rdečo barvo, zaradi lažje preglednosti, sem skrila graf prvega odvoda funkcije polinoma.

Rešitev točke c:

• Intervale konvekstnosti in konkavnosti funkcije sem poiskala s pomočjo definicije za konkavnost in konveksnost funkcije, ki pravi: Na intervalu, na katerem je f´´>0 , je funkcija f konveksna, na intervalu, na katerem je f´´<0, je funkcija f konkavna.

• Najprej sem po peš poti izračunala drugi odvod, nato pa še ničle drugega odvoda. Drugi odvod: Ničle drugega odvoda: -1.22, 0.55 Na intervalu x<-1.22 je f konveksna, predznak odvoda je pozitiven. Na intervalu -1.22<x<0.55 je funkcija konkavna, predznak odvoda je negativen. Na intervalu x>0.55 je funkcija konveksna, predznak odvoda je pozitiven

• Pri določanju konveksnosti in konkavnosti sem si pomagala z GeoGebro, tako da sem izračunala ničle drugega odvoda in izrisala funkcijo, ki sem jo dobila po izračunu drugega odvoda. Vendar sem zaradi lažje preglednosti prvotnega grafa polinoma skrila grafa funkcij prvega in drugega odvoda.

• LITERATURA: (Iz naslednje knjige sem uporabila tudi definicije, ki sem jih zapisala),Naslov:Matematika ODVOD/INTEGRAL, Avtorja:Peter Legiša, Ivan Štalec Založba in leto izdaje: DZS, Ljubljana 1986 Naloga: str. 102, 7.naloga