Besedilo naloge:
Določi gorišči in ekscentričnost elipse. Skiciraj tudi graf dane elipse:
Postopek reševanja naloge in rešitev:
Kaj sploh je elipsa:
Elipsa je množica ravninskih točk, za katere je vsota razdalj do dveh danih točk konstantna. Ti dve točki imenujemo gorišči elipse (G1 in G2). Torej: r1 + r2 = konst
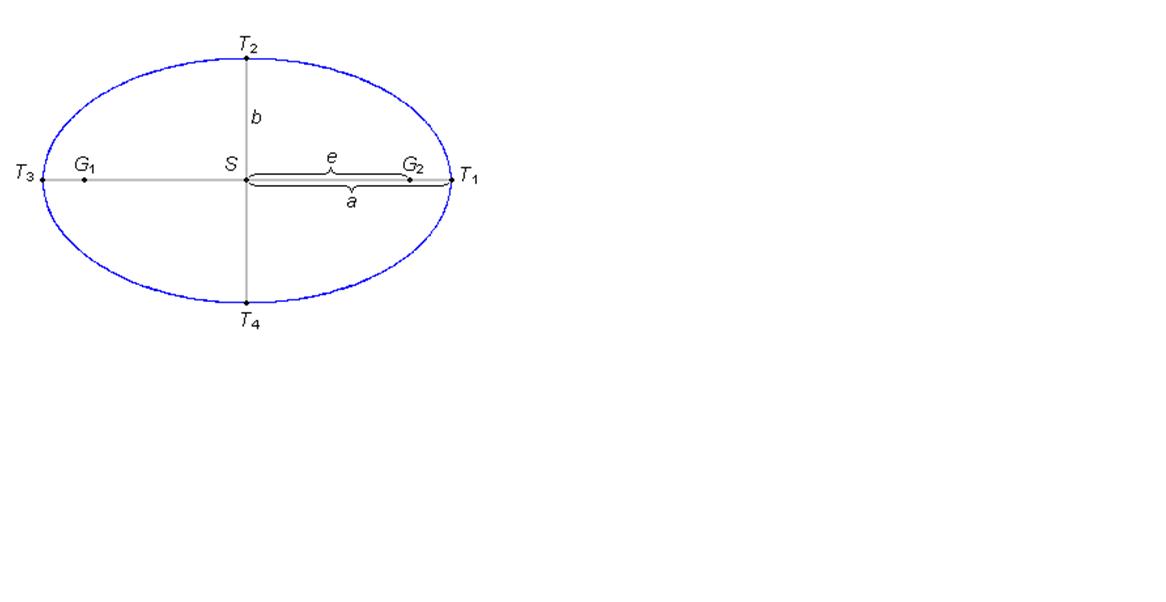
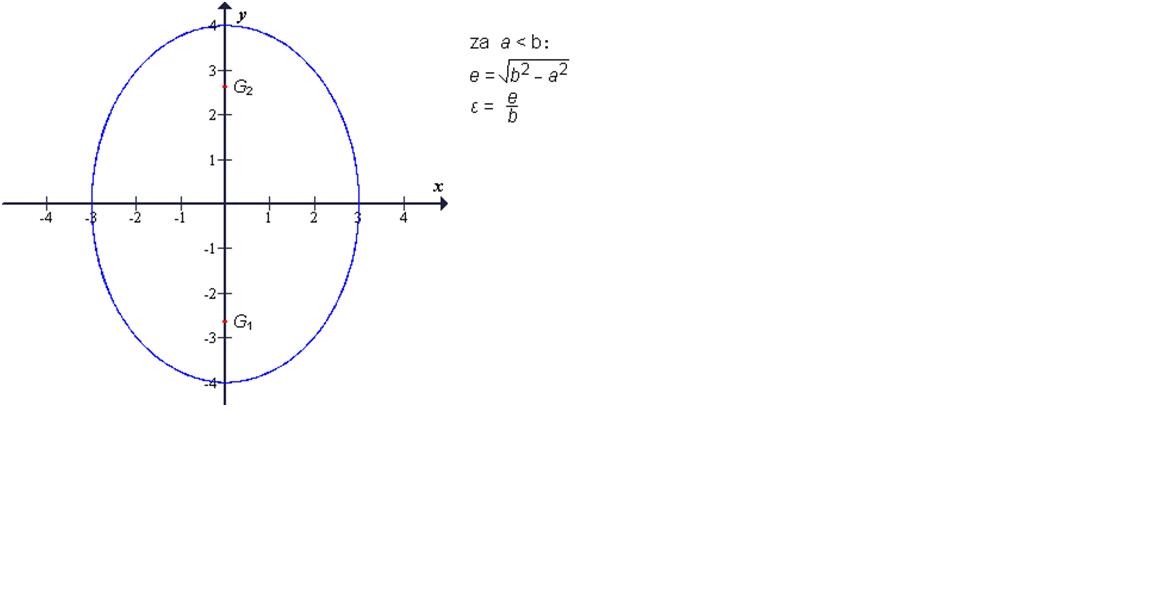
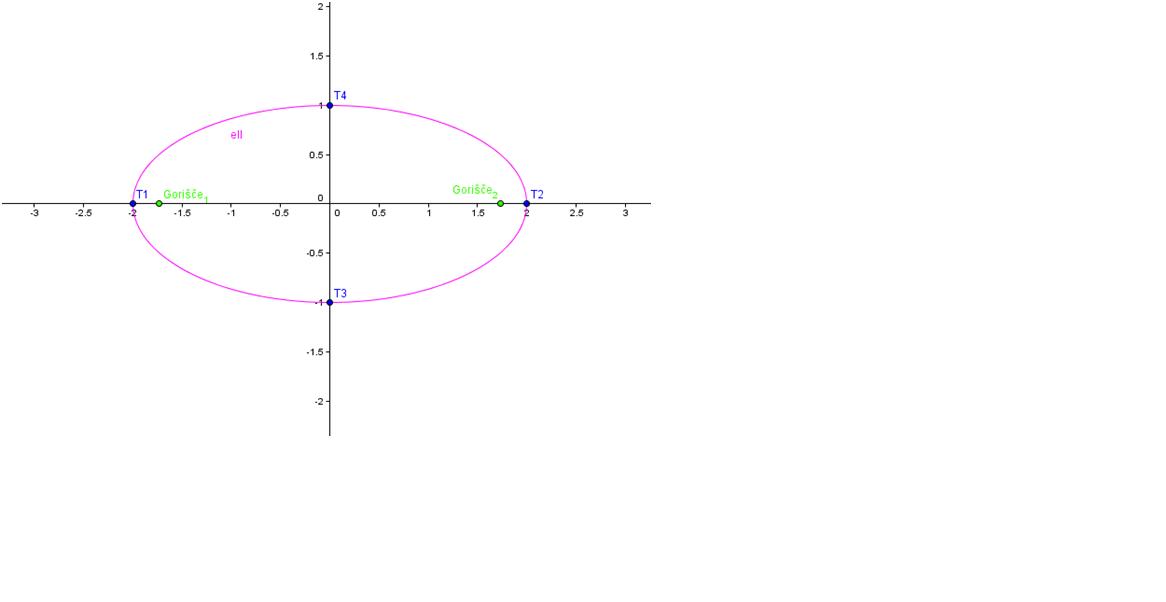
Elipsa ima dve simetrijski osi (simetrali). Njuno presečišče je središče elipse
(S). Točke, kjer simetrali sekata elipso, so temena elipse (T1, T2, T3, T4).
Razdalja od središča do bolj oddaljenega temena se imenuje velika polos elipse
(ponavadi jo označimo a), razdalja od središča do manj oddaljenega temena pa se
imenuje mala polos elipse (ponavadi jo označimo b).
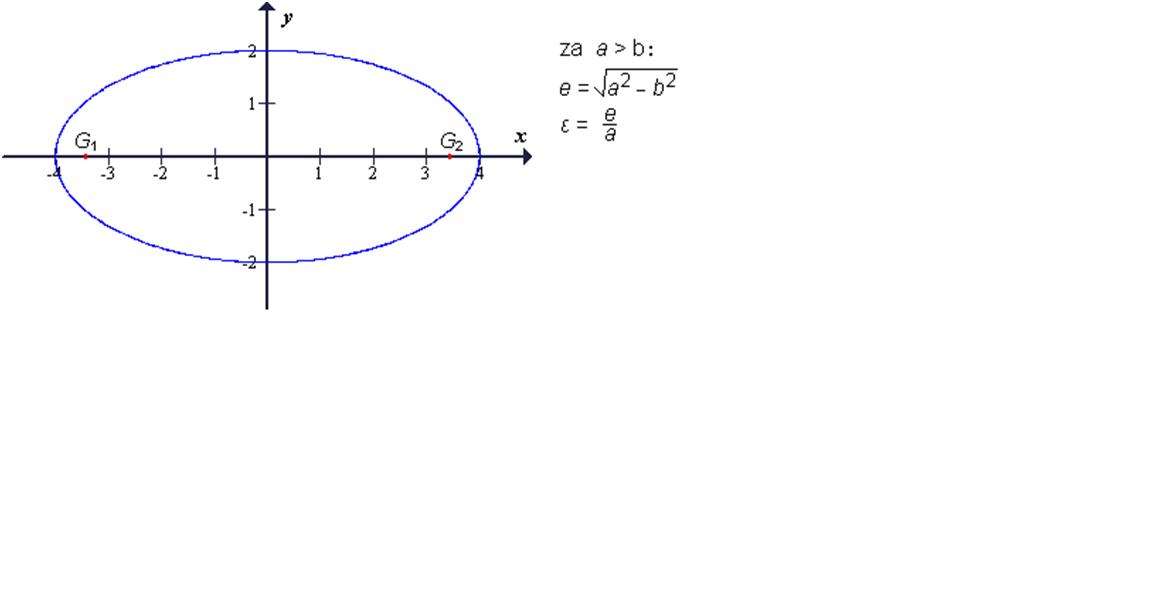
Gorišči elipse ležita vedno na veliki osi. Razdalja od središča do gorišča se
imenuje linearna ekscentričnost elipse (e).
Razmerje med linearnano ekscentričnostjo in veliko polosjo imenujemo numerična
ekscentričnost elipse (ε). Numerična ekscentričnost leži vedno na intervalu (0, 1)
in nam pove, kakšne oblike je elipsa. Če je ε blizu 0, je elipsa po obliki
podobna krogu; če je ε blizu 1, pa je elipsa zelo razpotegnjena (podolgovata).
Enačba elipse
Elipsa v središčni legi ima središče v točki S(0, 0), osi elipse pa ležita na koordinatnih oseh. Taka elipsa ima enačbo:
Ponavadi je velika polos a vodoravna, mala polos b pa navpična in veljajo zveze:
Včasih pa je a < b. To pomeni, da je velika polos navpična (b), mala polos pa vodoravna (a):
Če elipso vzporedno premaknemo tako, da pride središče v točko S(p, q), ima premaknjena elipsa enačbo:
Naloga:
Rešitev naloge v GeoGebri:
