Dani sta števili a=19323 in b=14809

1. Izračunajte največji skupni delitelj in najmanjši skupni večkratnik a in b.
2. Število n=a-b razcepite na prafaktorje. Zapišite vse delitelje tega števila.
3. Število n=a-b zapišite v dvojiškem zapisu.

Nalogo bomo reševali s pomočjo programa Matlab.

• Največji skupni delitelj je največje število, ki deli tako a kot tudi b.

  • Ukaz v Matlab-u: gcd(a,b)

• Najmanjši skupni večkratnik je najmanjše število, ki je deljivo z a in b.

  • Ukaz v Matlab-u: lcm(a,b)

Postopek reševanja v Matlab-u

Opis iskanja/računanja največjega skupnega delitelja in najmanjšega skupnega večkratnika.

To pomeni, da zapišemo število kot produkt samih praštevil.

• npr.: 12= 2*2*3 V Matlabu razcepimo število na prafaktorje s pomočjo funkcije factor(stevilo). Ta funkcija vrne matriko, ki jo sestavljajo prafaktorji števila:
• npr.: factor(12) vrne [2,2,4]

Postopek reševanja v Matlab-u:

Razbitje števila na prafaktorje.

Naše število 3514(n) lahko zapišemo kot 2*7*251.

• Delitelj celega števila n je število, ki deli n brez ostanka oz. ostanek je enak nič.
  V Matlabu sami »sprogramiramo« svojo funkcijo.
  

Dobro je vedeti:

• V Matlab-u je že definirana funkcija rem(a,b), ki vrne ostanek pri deljenju a:b.
• Če želimo napisati for zanko, je oblike for k=1:n. Ta for zanka bo "tekla" za vse k-je od 1 do n.
• Če želimo napisati pogojni stavek, je oblike if pogoj.
• Oba, for in if, zaključimo z značko end!
• Če želimo matriki A dodati na konec nek element a, naredimo to tako: A=[A, a]

Naša funkcija:

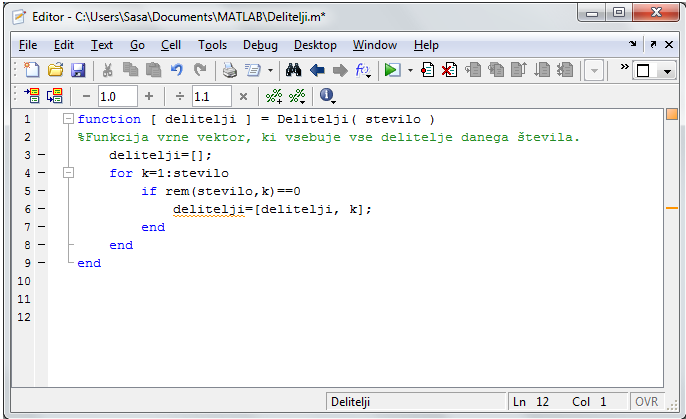
Sprehodimo se čez števila od 1 do n. Za vsako število preverimo, če je ostanek pri deljenju z n enak 0. Če ta pogoj drži, potem je to naš delitelj in ga dodamo matriki v katero shranjujemo delitelje. Na koncu vrnemo to matriko.

Funkcija, ki poišče vse delitelje danega števila.

Klic naše funkcije Delitelji(stevilo)

Klic funkcije in rezultat.

Delitelji števila 3514(n-ja) so: 1,2,7,14,251,502, 1757 in 3514.

Dvojiški oz. binarni sistem je številski sistem z osnovo 2. V dvojiškem zapisu se pojavljata le dve števki, 0 in 1.

Postopek za pretvorbo iz desetiškega v dvojiški sistem:

• Desetiško število delimo z 2. Napišemo celoštevilčni količnik in prištejemo ostanek.

  • Možen ostanek je le 0 in 1.
• Celoštevilčni količnik ponovno delimo z dve in spet zapišemo rezultat kot celoštevilčni količnik in ostanek.

• Postopek ponavljamo, dokler ne dobimo količnik 0 ali 1.

  • Ko je količnik 1 brez ostanka, je postopek končan. V primeru, ko je količnik z ostankom 1, ta ostanek z dve. Zapišemo 0+1.
• Dvojiški oz. binarni številski sestav dobimo tako, ostanke odčitamo po vrsti od spodaj navzgor.

Primer za število n oz. 3514:

Pretvorba iz desetiškega v dvojiški sistem.

Postopek reševanja s pomočjo Matlab-a:

V Matlab-u je že definirana funkcija dec2bin(n), ki pretvarja v dvojiški oz. binarni sistem.

Pretvorba iz desetiškega v dvojiški sistem v Matlab-u.

Število 3514 je v dvojiškem sistemu enak 110110111010.