Dani sta funkciji in .
a) Izračunajte ničli funkcije in točki, v katerih doseže funkcija lokalna ekstrema. Narišite
graf funkcije .
b) Narišite graf racionalne funkcije . (Stacionarnih točk ni treba računati.)
c) Izračunajte ničli funkcije .
Matematična naloga N3
Matematična naloga N3
Andrej Pavšič
Navodilo naloge
Matematično ozadje
Ničle funkcije so presečišča funkcije z abscisno osjo, dobimo pa jih kot . Funkcija doseže lokalne ekstreme, kjer je njen prvi odvod enak 0. Z drugim odvodom pa določimo ali gre za maksimum, minimum ali prevoj.
Potek reševanja
a)
b)
c)
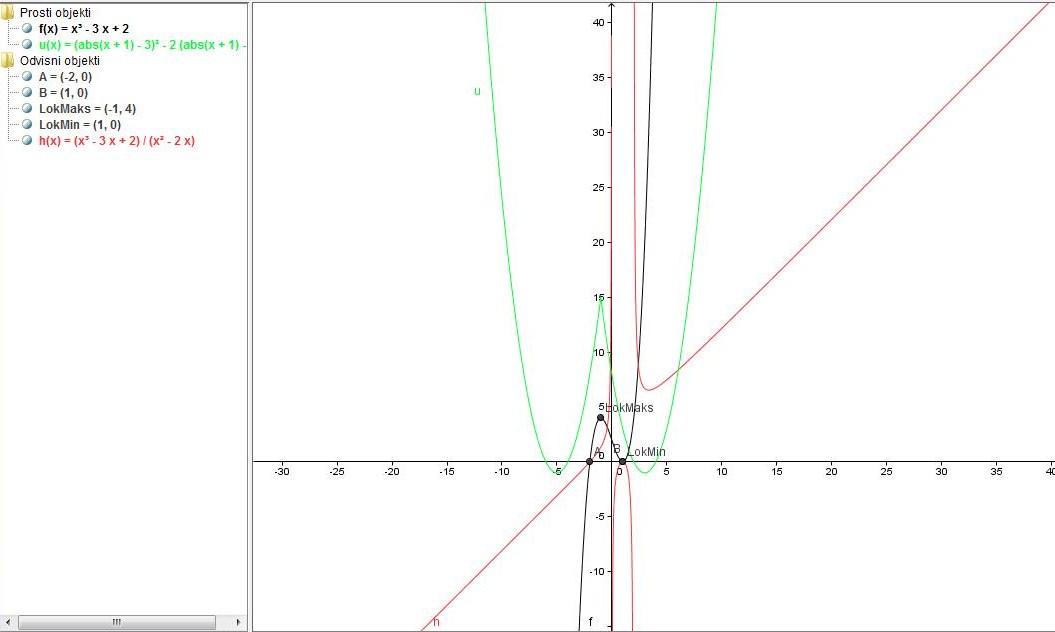
Funkcijo narišemo tako, da vsak , ki nastopa v zamenjamo z . V vnosno vrstico zato vnesemo izraz u(x)=(abs(x + 1) - 3)^2 - 2 (abs(x + 1) - 3), kjer abs(x+1) predstavlja absolutno vrednost . Tudi temu grafu priredimo drugo barvo zaradi boljše ločljivosti med grafi.
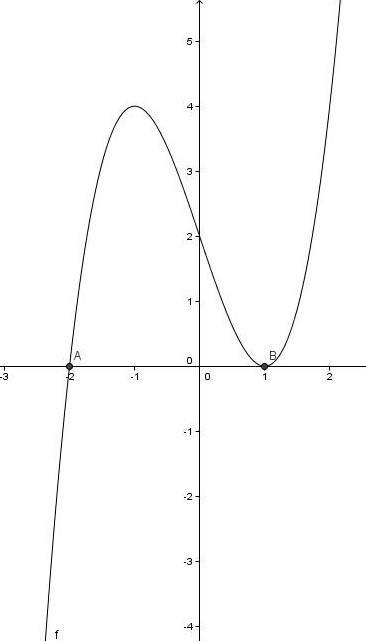
V vnosno vrstico vnesemo predpis za funkcijo z ukazom f(x)=x^3-3x+2. Ničle izračunamo z ukazom Nicla[f], lokalna ekstrema pa z ukazom Ekstrem[f]. Ničli sta točki in , ekstrema pa sta v točkah in . Zaradi boljše predstavnosti točki, ki nastopata kot ekstrema preimenujemo v LokMaks in LokMin. Ničla v točki je hkrati lokalni minimum.
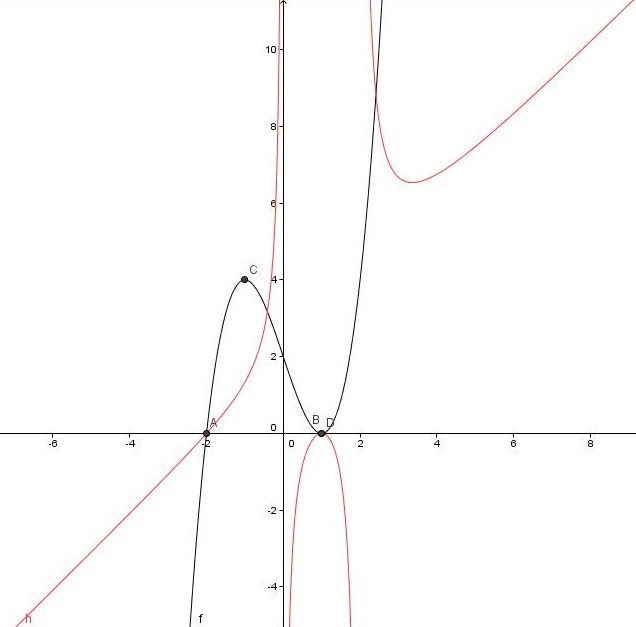
Graf racionalne funkcije narišemo z vnosom v vnosno vrstico. Funkcije ni potrebo vnašati kot x^3-3x+2, saj je že definirana med prostimi objekti.
Zaradi boljše ločljivosti med grafi graf obarvamo v drugo barvo. To storimo tako, da z desnim miškinim gumbom kliknemo na funkcijo in izberemo lastnosti. V lastnostih nato izberemo zavihek barva, kjer tudi izberemo želeni odtenek.
