Najpreprosteje bi se praktično lotili merjenja obsega s kolesom, ki bi ga kotalili po vodoravni podlagi in si označili začetek in konec enega polnega vrtlaja. To kaže spodnja animacija.

Kolikokrat se zavrti kolo na m dolgi poti, če so enote na zgornji sliki v dm?

Preveri

Pomagaj si z apletom in najdi kot zasuka kolesa, če kolo opravi pot dm. Kolikšno pot pa opiše kolo, če je kot zasuka . Zdaj pa še preveri dolžino loka pri , , , . Kot zaokroži na eno decimalko.

Če kolo opravi pot dm, opiše kot . Pri zasuku za kolo opravi pot dm. Dolžine poti, ki jih pri teh primerih lahko preberemo, so po vrsti dm, dm, dm, dm.

Preveri

Iz drugega dela naloge lahko sklepamo, da je sorazmerje med središčnim kotom in dolžino krožnega loka premo. Zaradi zaokrožitev te vrednosti niso natančne, zato pa ta premislek opravimo naravnost iz oblike krožnice - enakim središčnim kotom kjerkoli na isti krožnici pripada enak krožni lok.

Ti primeri kažejo, da je pogosto treba izračunati dolžino dela krožnice - krožnega loka. Tak del krožnice izrazimo s pripadajočim središčnim kotom. ker dolžina krožnega loka enakomerno narašča, Če poznamo ta kot, Potem pa je dolžina pripadajočega loka enaka deležu obsega, ki je enak deležu središčnega kota glede na polni kot.

Tetiva je daljica, ki povezuje krajišči krožnega loka. Njeno dolžino zopet izračunamo s pomočjo središčnega kota in kosinusnega izreka. V posebnem primeru je dolžina tetive enaka premeru kroga.

Vsak krogu včrtan večkotnik lahko s središčnim raztegom preslikam v podobni večkotnik, katerega obseg se tudi pomnoži s faktorjem središčnega raztega. Tudi ta raztegnjen večkotnik bo še vedno včrtan krogu. Torej lahko sklepamo, da se bo tudi obseg tega očrtanega kroga pomnožil s podobnostnim koeficientom središčnega raztega. To bi lahko dokazali z včrtovanjem večkotnikov z zelo majhnimi dolžinami stranic, ki pa so že zelo dobri približki za dolžino obsega kroga, kot se lahko prepričamo na zgornji animirani sliki.

Ker se pri podobnosti tudi premer kroga pomnoži z istim faktorjem, je razmerje med premerom kroga in njegovim obsegom konstantno. V primeru iz praktičnega merjenja obsega zgoraj lahko to razmerje izračunamo. Če smo s kotaljenjem kolesa po ravni podlagi izmerili njegov obseg (v našem primeru je bilo to dm) in izmerimo še njegov premer (v našem primeru je to dm), dobimo za naše merjenje:

Če smo še malo bolj natančni in izmerimo premer kolesa na mm, dobimo:

kar pa je že zelo dober približek za , ki je ta kvocient.

Število je transcendentno število. Njegova zgodovina je kar obsežna in je prinesla veliko vzpodbud v matematični zgodovini. Stari Egipčani so na primer ocenili, da je ploščina kroga s premerom enaka:

iz česar po kratkem računu pokažemo, da so imeli sorazmerno slab približek za , saj odtod dobimo, da je po njihovem .

V Indiji so matematiki računali s približkom , kar je podobno kot v starem Egiptu, že Arhimed pa je s praktičnim računanjem obsegov krogu včrtanih in očrtanih večkotnikov ocenil z oceno:

kar je že ocena za med in .

Okrog leta 500 našega štetja so na Kitajskem obravnavali kot približek za , kar pa je s že kar zavidljiv, na šest decimalk natančen približek.

Mnogo kasneje so, tudi z razvojem višje matematike izračunavali vse boljše in boljše približke za število . Tudi naš Jurij Vega je imel s izračunanimi decimalkami dolgo časa najboljši približek zanj.

Danes seveda tudi s pomočjo računalnikov izračunajo število na milijardo decimalk, seveda pa je to brez kakršnekoli praktično uporabne vrednosti.

Če vzamemo, da se zgornji avtomobil giblje s konstantno hitrostjo in poznamo premer koles (naj bo to v našem primeru cm), lahko izračunamo, kako hitro se vrtijo njegova kolesa - bolj natančno, kolikokrat v sekundi se zavrtijo. Najpreprosteje bomo to opravili tako, da bomo izračunali, kolikokrat gre obseg kolesa v prevoženo pot in potem iz časa, potrebnega za to pot izračunali koliko časa potrebuje kolo za en obseg in s tem dobili tudi število obratov kolesa v časovni enoti. V ta namen ustavimo zgornji aplet v nekem trenutku in preberemo potrebne podatke: če avto opravi pot m, je porabil čas s. Tedaj dobimo:

Iz tega dobimo približno obratov kolesa v sekundi.

Opomba: včasih so merilci hitrosti v avtomobilu delovali tako, da so merili število obratov v časovni enoti. Če bi zamenjali kolesa za večja ali manjša, tak merilnik seveda več ne bi deloval pravilno.

Merilec hitrosti avtomobila ima nastavljen merilec števila obratov in ta kaže pri hitrosti obrata na sekundo. Koliko obratov bi morali nastaviti, če zamenjamo kolesa tako, da se njihov polmer poveča za cm?

Preveri


Kolo bicikla ima premer cm. Z biciklom smo prevozili km. Kolkokrat se je kolo zasukalo? Rezultat z decimalno vejico zapiši na eno decimalko.

Kolikokrat pa zasučemo pedale, če je polmer zobnika cm?

Kolo se je zasukalo krat.

Pedale bi zasukali krat.

Preveri

Krožnica s polmerom cm. Koliko meri obseg tega kroga? Kolikšen bi moral biti polmer, da bi obseg meril cm?

Obseg kroga meri:

Preveri

Polmer v drugem primeru je:

Preveri

Obseg kroga meri cm. Kolikšen lok pripada središčnemu kotu ?

Kotu pripada lok

Preveri

Kolikšen središčni kot pripada loku cm v krogu, katerega polmer je cm?

Lok cm pripada središčnemu kotu

Preveri

Izračunaj dolžino tetive v krogu, ki pripada središčnemu kotu . Polmer preberi iz slike.

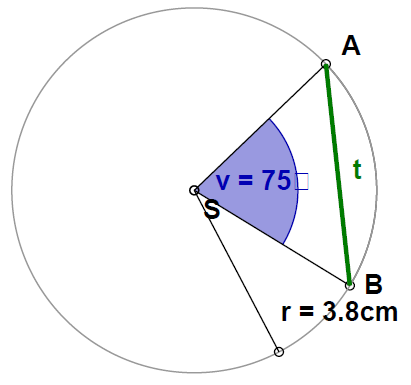
Dolžina tetive je

Preveri

Avto prevozi pot km. Kolikokrat se na tej poti zavrti kolo s premerom cm?

Kolo s premerom cm se na km poti zavrti

Preveri

Za merilec hitrosti vemo, da pokaže pri neki hitrosti avtomobila obratov kolesa v sekundi. Kolikšna je hitrost avtomobila, če je polmer kolesa cm. Izrazi hitrost v in .

Hitrost avtomobila je

Preveri