Navodilo naloge
V pravokotnem koordinatnem sistemu v prostoru imamo točke , in . Krajevne vektorje teh točk označimo , in .
a) Za kateri vrednosti realnega števila je dolžina vektorja enaka 11?
b) Izračunajte realno število tako, da bo trikotnik pravokoten s pravim kotom pri oglišču .
c) Naj bo . Pokažite, da ležijo v tem primeru vektorji , in v isti ravnini.
Matematično ozadje
a) Dolžino dimenzionalnega vektorja izračunamo po formuli: ||||.
b) Dva vektorja sta med seboj pravokotna, če je njun skalarni produkt enak 0. Ker imamo podane le krajevne vektorje in ker vemo, da je pravi kot v oglišču C, potem določimo vektorja in takole: , .
c) Trije vektorji ležijo v isti ravnini, če je njihov mešani produkt enak 0.
Potek reševanja
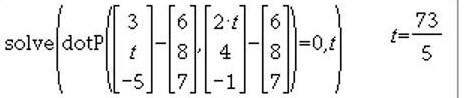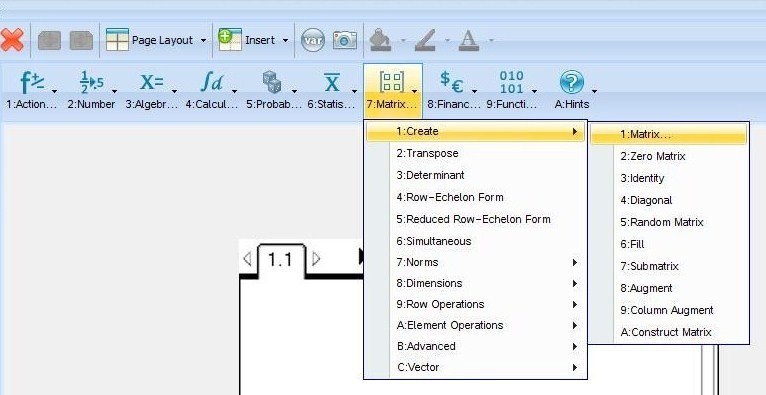
Vektorje v TI-Nspire ustvarimo kot matriko .
a)
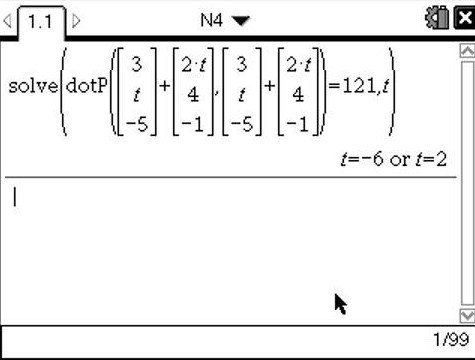
Dolžina vektorja na kvadrat je enaka skalarnemu produktu . Ker bomo reševali enačbo, uporabimo ukaz solve(»Enačba«, »spremenljivka«), kjer bo enačbo predstavljal na levi strani skalarni produkt, na desni dolžina na kvadrat, spremenljivka pa je v našem primeru označena s črko . Skalarni produkt pa vnesemo z ukazom dotP(vektor1, vektor2). Ker pri skalarnem produktu dobimo kvadratno enačbo, sta rešitvi za enaki 2 in -6.
b)
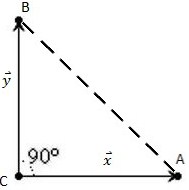
V trikotniku določimo vektorja in , kjer oba izhaja iz točke oz iz krajevnega vektorja točke . Tudi tukaj bomo reševali enačbo, kjer bomo skalarni produkt vektorjev in enačili z 0, iskali pa bomo . Uporabimo enaka ukaza kot v primeru a) in vnesemo vektorja in v skalarni produkt. Kadar je enak , sta vektorja in pravokotna oz. je trikotnik pravokoten.
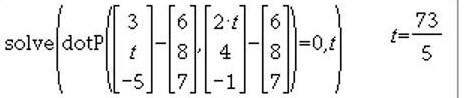
c)
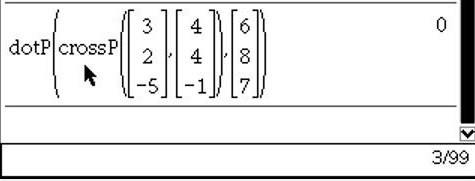
Če vektorji , in pri ležijo v isti ravnini, potem mora biti njihov mešani produkt enak 0. Vstavimo v vektorja in , nato pa izračunamo mešani produkt . Vektorski produkt izračunamo z ukazom crossP(vektor1, vektor2).
