Zapišite enačbi tistih dveh tangent na graf funkcije , ki sta vzporedni premici .
Matematična naloga N5
Matematična naloga N5
Andrej Pavšič
Navodilo naloge
Matematično ozadje
Tangento določimo s smernim koeficientom in eno točko, ki leži na tangenti, in je oblike . Ker sta iskani tangenti vzporedni dani premici, imata tudi enak smerni koeficient . Točko bomo dobili tako, da bomo enačili smerni koeficient tangente s prvim odvodom . Ker je prvi odvod polinoma tretje stopnje polinom druge stopnje, bomo dobili dve točki, kateri bomo vstavili v enačbo tangente ter tako dobili še začetno vrednost .
Potek reševanja
V GeoGebri narišemo funkcijo z ukazom . Njen odvod izračunamo z ukazom Odvod[f(x)]. To nam izriše funkcijo . Ker nas graf odvoda ne zanima, ga skrijemo. Na graf kliknemo z desnim miškinim gumbom in izberemo lastnosti. Pod rubriko osnovno odznačimo Prikaz objekta.
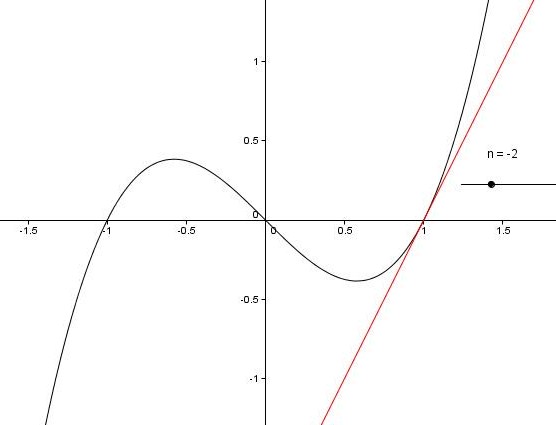
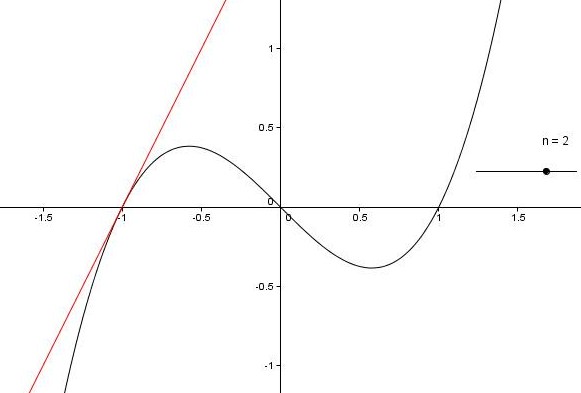
Narisati moramo še tangento , zato najprej ustvarimo drsnik na intervalu in nato še premico z ukazom . S premikom drsnika lahko predpostavimo, da sta iskani tangenti oblike in .
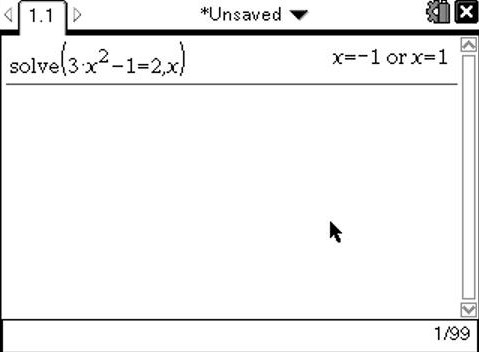
Računsko lahko to preverimo tako, da prvi odvod enačimo s koeficientom tangente. Tako dobimo koordinati točk, ki pa sta enaki kot na sliki: in .
|
|
