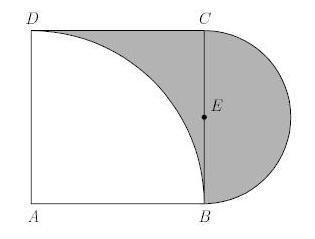
Stranica kvadrata meri 4 enote. Narisana sta dva krožna loka (glejte sliko). En krožni lok ima središče v točki , drugi pa v razpolovišču stranice . Izračunajte natančno ploščino osenčenega lika na sliki.
Navodilo naloge
Stranica kvadrata meri 4 enote. Narisana sta dva krožna loka (glejte sliko). En krožni lok ima središče v točki , drugi pa v razpolovišču stranice . Izračunajte natančno ploščino osenčenega lika na sliki.

Matematično ozadje
Ploščino kvadrata izračunamo kot kvadrat stranice , ploščino kroga pa kot produkt števila s kvadratom polmerom kroga.
Potek reševanja
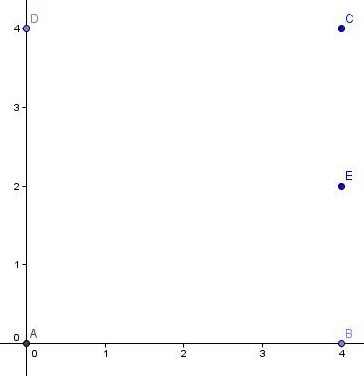
V GeoGebri najprej narišemo točke , , , in . Nato ustvarimo daljice , , in ter mnogokotnik , ki ga te daljice omejujejo. Ploščina tega kvadrata je 16.
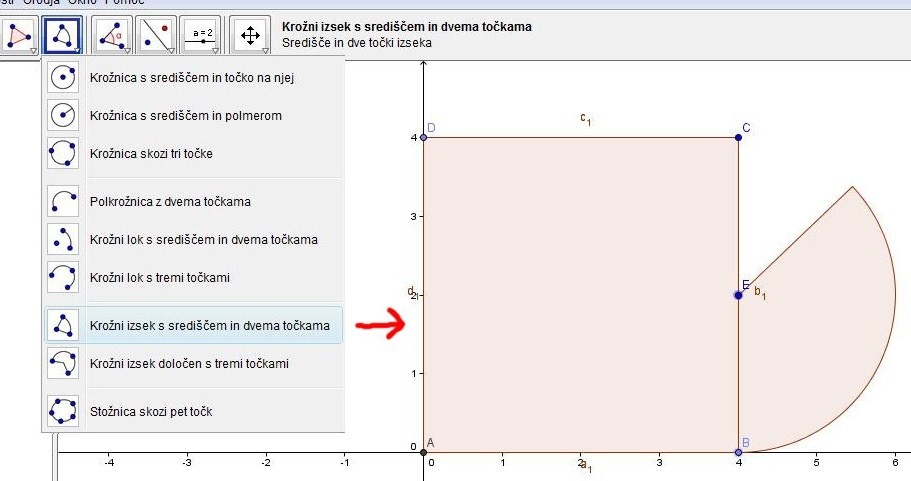
Ker v GeoGebri ne moremo računati ploščine polkroga, ki ga skonstruiramo s polkrožnico, za konstrukcijo krožnega loka s središčem v izberemo ukaz Krožni izsek s središčem in dvema točkama. Isti ukaz izberemo za konstrukcijo krožnega loka s središčem v točki .
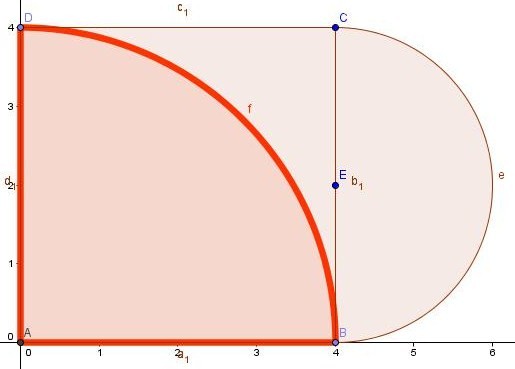
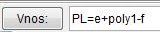
Za lažjo predstavo spremenimo barvo (lahko tudi debelino črte) krožnemu izseku . Ploščine krožnih izsekov so bile izračunane že ob konstrukciji, tako da vrednosti med sabo samo še seštejemo oz. odštejemo. V vnosno vrstico vnesemo enačbo PL= e+poly1-f, kjer je e ploščine krožnega izseka , poly1 ploščina kvadrata in f ploščina krožnega izseka . Izračunan rezultat je 9,72, saj GeoGebra za uporablja približek 3,14.
Natančen izračun bi se glasil .